摘 要

介绍了欧式期权定价的相关因素，在所有因素之中，唯一不确定的因素来自于波动率；之后介绍了与波动率相关的几种期权定价模型；利用ETF50期权的数据实证研究验证了不同模型定价的有效性，并对实证结果提出了解释原因；并对波动率的结构进行了深一步的研究，利用ARCH模型、EWMA模型、GARCH模型从一维的角度对波动率进行了预测；总结了构建了三维度波动率曲面的相应数值方法；对未来波动率模型的修近提出了自己的看法。

关键词：局部波动率方程; 隐含波动率; 波动率曲面

Abstract

This paper introduces factors of several options pricing models related to a uncertain variable—volatility , validates the effectiveness of different model pricing by using the empirical research of ETF50 option, and puts forward the explanational reasons for the empirical results, and makes a deep research on the structure of volatility, using ARCH model, EWMA model, and GARCH model to predict the volatility from a one-dimensional point of view, summarizes the corresponding numerical methods of constructing the three-dimensional volatility surface, and puts forward views on the revision of the future volatility model.

Key words: Local volatility equation ; implied volatility ; volatility surface

目 录

第一章 绪论 1

1.1 选题背景 1

1.2 研究方法与研究思路 1

1.3国内外研究动态 1

1.3.1国外研究现状 1

1.3.2国内研究现状 2

第二章 定性分析期权定价的影响因素 4

2.1.期权定价定性分析 4

2.1.1期权定价中不确定的波动率 4

2.2以收益率波动率为发展基线的模型分析 5

2.2.1.布兰克-斯科尔斯模型基础 5

2.2.3.Heston模型基础 5

2.2.4.跳扩散过程 7

2.2.5.SVJ模型 7

第三章 分析不同期权定价模型的效率 8

3.1.数据样本选择 8

3.1.1选择原因 8

3.1.2 选择时间 8

3.2实证分析 9

3.2.1.实证分析 9

3.2.2.原因探索 10

第四章 基于实证结论的波动率结构探索——一维波动率预测模型构建 11

4.1.关于ETF基金（510050）时间序列研究 11

4.1.1描述性统计 11

4.1.2.ARCH 11

4.1.3 实证结果 12

4.2 EWMA 模型 13

4.2.1 EWMA 模型 13

4.2.2 实证分析 14

4.3.GARCH模型 15

4.3.1 GARCH模型 15

4.3.2.实证研究 15

第五章 三维波动率曲面构建 16

5.1三种构建方法 16

5.1.1.市场模型 16

5.1.2.Vega-Gamma-Vanna-Volga模型 16

5.1.3.因子模型 16

5.1.4.模型不足 17

第六章 总结与展望 18

6.1.总结 18

6.2.展望 19

参考文献 20

附录 22

致谢 24

第一章 绪论

1.1 选题背景

改革开放以来，中国逐步建立起市场经济制度，然而金融市场的发展还是相对滞后的。金融衍生品在金融市场中有着重要的角色。尽管中国的金融衍生品发展尚处于初级阶段，业界越来越重视金融衍生品的定价问题。ETF50基金2004年1月2日正式发行，以复制上证50指数的方式定价，并且可以在二级市场自由买卖。在不断开放且瞬息万变的金融市场的过程之中，对于金融衍生品更加准确的定价可以促进金融市场的流动性，提高金融交易的效率，并且减少交易的成本。本文以ETF50期权以及其标的资产的相关数据为基础，根据布兰克-斯科尔斯期权公式和海斯顿模型来分析比较相关期权定价方案的可行性与准确性，并且根据实证研究数据，进一步细化研究影响标的资产波动率的相关因素，提出可行的改进方向。

1.2 研究方法与研究思路

1.2.1.为了更好的拟合波动率时间序列，放弃了差分方程，而采用了微分方程来建立模型并衡量波动率的变化。

1.2.2.针对不同的波动率模型，采用解析解或者数值解两种方法来解决微分方程，并且比较不同数值方法之间的区别。

1.2.3.利用的传统数值方法包括蒙特卡洛模拟来拟合随机过程、利用傅里叶变换来加速处理随机波动模型的特征函数。

1.2.4.通过统计学实证研究判断不同的假设条件对于不同波动率模型的有效性。

1.3国内外研究动态

1.3.1国外研究现状

斯波林科,艾利斯,博耐斯,萨缪尔森,鲍穆尔,马基和库特,陈已经就权证定价给出了相关解，不足之处在于他们的解析解中包含一个或多个随机参数^[1]。1973年，布兰克和斯科尔斯从索普和卡索夫的角度重新审视期权定价问题^[2]。索普和卡索夫利用拟合期权价格曲线的方法确定出期权和标的资产的无风险收益组合之中各部分之比例^[3]，布兰克和斯科尔斯进一步补充该组合的收益率应该满足无风险收益率。并结合他们提出的七条假设条件，推导出了布兰克-斯科尔斯公式的偏微分方程。通过公式的变形，将偏微分方程便为标准的热传导方程，并且给出了期权定价的解析解。在布兰克-斯科尔斯模型的出现为业界提供了期权定价的解析解，促进了金融市场定价效率的提高，在已知标的资产价格、行权价格、无风险利率、标的资产价格波动率、剩余到期时间的情况下，可以通过布兰克-斯科尔斯公式求出模型假设条件下的精确期权价格，但是布兰克-斯科尔斯公式存在的诟病主要来自于相关参数的可获得性与准确性，其中之一在于对标的资产波动率的常数假设并不与现实相符。在1987年股灾之后，人们第一次注意到了隐含波动率的非常数假设，并得到了微笑曲线，并且将波动率的研究从二维拓展到了三维。在实际金融市场之中，人们发现期权波动率具有波动率聚类、自相关性以及尖峰厚尾分布，根据这三项特征,威尔莫特提出了一个随机微分方程组用来描述上述波动性，并得到了与BS公式相似的拥有两个随机项的无风险收益组合^[4]。继BS模型提出解析解之后，关于波动率更细一步的研究来自于杜皮尔.杜皮尔和德曼、卡尼注意到局部波动率方程是与风险中性测度下密度函数一一对应的^[5] 。吉姆.盖塞罗基于此推导了局部波动率与隐含波动率的关系，以及局部方差与瞬时方差的联系^[6] 。考克斯和罗斯 提出了CEV模型，放弃了标的资产常数波动率的假设^[7]。赫尔,怀特建立了新的随机波动率模型，但不足之处在于没有解析解并且数值方法需要处理二维变量，操作难度大^[8]海斯顿从股价的几何扩散模型出发，同时假设了瞬时方差的变动服从Ornstein-Uhlenbeck过程，即波动率满足均值回归性质。类比于Heston模型的封闭解结论，海斯顿模型在变换过程上更加方便。通过傅里叶变换和相应的边界条件，求得了相应概率的函数表达式 ^[9]。盖赛罗提供了一种参数化的方式SVI，随机波动率激发的参数化形式，这种参数化方式在长期体现了较好的拟合效果，但短期来看，无法很好的描述波动率曲面的相关形态^[10]。在海斯顿模型的基础之上，海斯顿和南迪研究了ρ=-1的情形，并给出了用近似公式计算局部方差的合理性^[11]。基于上述短期波动率曲面无法拟合实际曲线，威尔米特介绍了跳扩散过程，并假设跳跃强度服从泊松分布，但是无法确定跳跃的幅度与方向，此时跳跃强度J是一个均值为0的随机离散项^[12]。在理论上得到了跳扩散模型之下，金融资产的定价公式。莫顿构建了跳跃-扩散模型，在跳跃幅度满足对数正态分布的条件下，推导出了欧式期权的解析解。陈在随机波动率模型的基础上引入跳过程（SVJ），此改进已被实证证明优于海斯顿模型^[13]。哈干、库玛、勒斯尼斯基、伍德沃德针对短期波动率曲面的拟合效果，提出了SABR模型，给出了短期波动率曲线的函数表达 ^[14]。

1.3.2国内研究现状

邓力研究了上证ETF50期权波动率曲面的构建方法，并基于此提出了稳定性改进方案；同时，他也解释了波动率曲面的客观规律，并且初步推测了出现上述现象的原因 ^[15]。林先锋对上证ETF50期权的波动率曲面形态进行了描述，阐述了隐含波动率向右上方偏斜的一个重要因素是隐含分布存在一定的右部厚尾特性 ^[16] 。陈思系统总结了构建波动率曲面的五大方法并进一步比较了不同方法的拟合精度、计算速度、稳定性和合理性；详细阐述了构建波动率曲面的常见问题以相应的解决方案；深入探索动态隐含波动率曲面，介绍三种隐含波动率曲面建模方法；利用标普500指数的实证分析验证了一般化动态隐含波动率因子模型的实证意义^[17]。毛娟通过函数型分析降低了波动率曲面的维度，通过几个因子体现了波动率曲面的特征，方便了投资分析；相对于传统的多元数据分析，函数型数据分析往往更加有效直观；并且利用matlab编程实现了隐含波动率的函数型主成分分析，也指出了进一步的研究方向^[18]。

第二章 定性分析期权定价的影响因素

2.1.期权定价定性分析

2.1.1期权定价中不确定的波动率

对于欧式看涨期权来说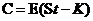，，在其他因素不变的情况下，

1.敲定价格越小，欧式看涨期权价格越高

2.标的资产的价格越大，期权的价值越高

3.无风险利率越高，欧式看涨期权价值越高

4.距离到期时间越长，欧式看涨期权价值越高

5.标的资产波动率越高，欧式看涨期权价值越高

在上述五项关键影响因素中，敲定价格、标的资产价格、无风险利率和剩余时间是易于获取的准确数据；对于标的资产的收益率波动率，最初布兰克-斯科尔斯的常数假设已被证实存在误区，波动率是难以准确测量的，业界开始研究波动率对于期权价格的影响。

在局部波动率的研究上，与海斯顿模型相似，杜皮尔在研究局部波动率方程的时候也采取了最开始的标的资产的股价满足几何布朗运动。用概率密度的方法来表示欧式看涨期权的价格可以写成^[5]

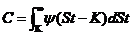（2.1）

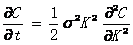其中代表标的资产价格在行权的时刻的概率密度函数，还应该满足福克-普朗克方程。通过以上，我们可以得到相关的表达式：

（2.2）

关于波动率的表达式可以表示为

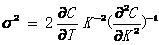（2.3）

然而此表达式并不能表达隐含波动率，严格来说局部波动率是在风险中性测度下，远期价格等于执行价格时，瞬时方差的条件期望。隐含波动率的确定与布兰克-斯科尔斯公式有着极强的联系。布兰克-斯科尔斯公式第一次提供了相关的欧式看涨期权的解析，也是金融市场关于期权报价的基本模型。因此，隐含波动率的表达需要根据布兰克-斯科 尔斯公式的解析解来确定。定义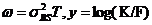 局部波动率与隐含波动率存在一定联系，考虑特殊情况,局部方差在时间上的积分与总体隐含方差完全相同，即

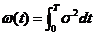（2.4）

2.2以收益率波动率为发展基线的模型分析

2.2.1.布兰克-斯科尔斯模型基础^[2]

对于布兰克-斯科尔斯模型，其特征函数满足：

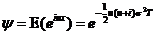（2.5）直接利用傅里叶变换可以得到布兰克-斯科尔斯公式。

通过对冲掉随机波动项并且满足风险中性的条件下，可以得到关于期权价格的偏微分方程：

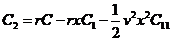（2.6）

其中c表示欧式看涨期权的价格，下标1，2分别表示对t和x的偏导数，v代表波动率，x代表表的资产的价格。

除此之外，还满足边界条件：

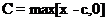（2.7）

通过合适的替换，可以将上式表达式转换成标准的热扩散过程，即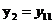的形式。

最终可以得到

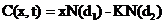（2.8）

对于欧式期权定价中的五个变量里的时间、波动率的平方、利率而言，欧式期权的价格会随着这些变量的增加而变大。欧式期权的价格对于标的资产的偏导数恰恰等于负无穷到d1的累计标准正态分布。

2.2.3.Heston模型基础^[9]

Heston提出的动态过程抛弃了相关的波动率常数假设：

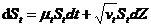（2.9）

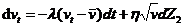（2.10）

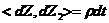（2.11）