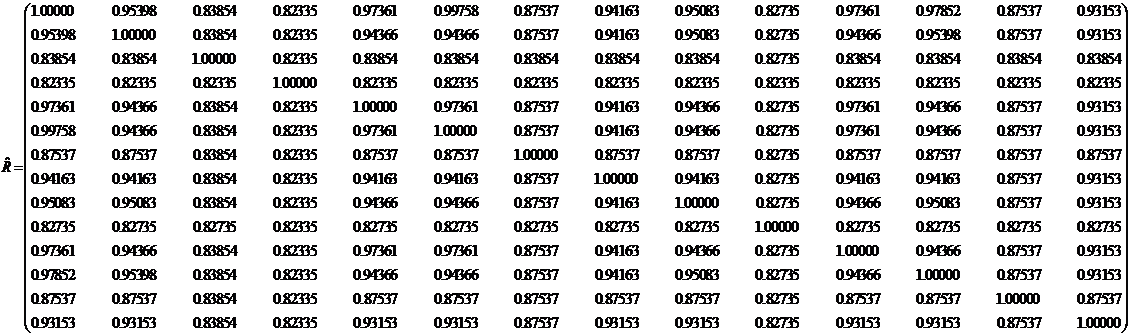无监督算法研究毕业论文
2020-04-09 13:59:19
摘 要
在数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断等领域中,机器学习往往扮演着不可替代的角色,本文的主题是当下热门的一种机器学习技术,无监督学习。
本次论文对几种典型的无监督算法进行了学习,并针对一些典型问题进行了仿真研究:介绍了传统的图像分割与聚类算法分割,并利用基于K-均值聚类算法的图像改进分割方法进行了图像分割;围绕层次聚类分析算法展开研究,将层次聚类分析方法应用在电价区域的空间尺度划分问题中,进而实现了电价区域的划分;运用模糊聚类的方法,根据动态聚类图对人脸图像进行分类。
关键词:聚类算法;K-均值聚类;层次聚类;模糊聚类
Abstract
In many fields such as data mining, computer vision, natural language processing, biometrics, search engines, medical diagnosis, etc., machine learning often plays an irreplaceable role, and the topic of this thesis is a popular machine learning technology. Supervise learning.
In this thesis, several typical unsupervised algorithms are studied and some typical problems are simulated. The traditional image segmentation and clustering algorithm segmentation is introduced, and the improved image segmentation method based on K-means clustering algorithm is introduced. Image segmentation was performed and research was conducted around hierarchical clustering analysis algorithms. Hierarchical clustering analysis method was applied to the problem of spatial scale division of electricity price regions, and then the division of electricity price regions and the method of using fuzzy clustering were implemented, according to dynamic clustering. The figure categorizes face images.
Key Words:Clustering Algorithm;K-means clustering;Hierarchical clustering;Fuzzy clustering
目 录
第1章 绪论 1
1.1 目的及意义 1
1.2 国内外研究现状 1
1.3 研究的基本内容 2
第2章 基于K-均值聚类的图像分割算法 3
2.1 K-均值聚类算法 3
2.2 基于K-均值聚类的彩色图像分割算法及改进 3
2.2.1 图像特征提取 4
2.2.2 K-均值聚类图像分割算法的研究与改进 5
2.2.3 实验结果与分析 6
第3章 基于尺度空间层次聚类的电价区域划分 7
3.1 层次聚类分析算法 7
3.2 层次聚类分析算法的有效性研究 7
3.2.1 有效性函数的定义 8
3.3 尺度空间理论 9
3.4 基于尺度空间层次聚类的电价区域划分 11
3.4.1 聚类样本 11
3.4.2 基于尺度空间的区域划分 11
3.4.3 聚类的有效性 12
3.5 本章小结 14
第4章 基于模糊聚类的人脸图像分类 15
4.1 模糊集合 15
4.1.1 模糊子集的概念 15
4.1.2 模糊关系 15
4.1.3 运用传递闭包法进行模糊聚类 16
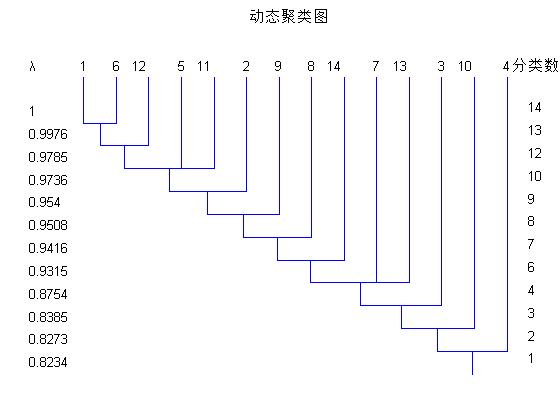
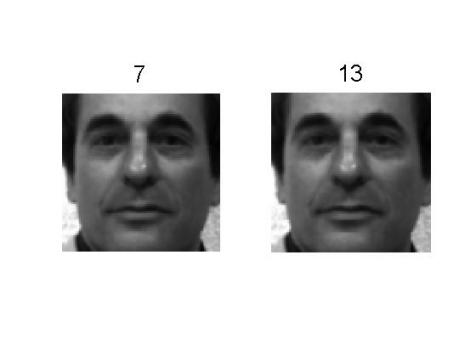
4.2 基于模糊聚类的人脸图分类 17
4.3 基于模糊聚类的人脸分类算法设计 18
4.4 实验仿真 18
第5章 结论 22
参考文献 23
致 谢 24
第1章 绪论
1.1 目的及意义
在现实生活中,往往存在这样的问题:缺乏足够的先验知识,难以人工标注类别;人工类别标注的成本过高。自然的,我们希望计算机能代我们(部分)完成这些工作,或至少提供一些帮助。无监督算法对于处理这类问题显得尤为重要,我们所做的无监督学习就是根据它们的性质自动地将它们分成若干组,它们都具有相似的性质(如数学问题会集中在在一组,英语问题会集中在在一组,物理......)。所有数据只有特征向量没有标签,但是可以发现这些数据呈现出聚群的结构,本质是一个相似的类型的会聚集在一起。把这些没有标签的数据分成一个一个组合,就是聚类。比如谷歌新闻,每天会搜集大量的新闻,然后把它们全部聚类,就会自动分成几十个不同的组(比如娱乐,科技,政治......),每个组内的新闻都有相似的内容结构。常用的应用背景包括:从大量样本中选择具有代表性的分类器,用于分类器的训练;在没有类别信息的情况下寻找好的特性。
需要说的是,相比有限的监督学习数据,自然界有无穷无尽的未标注数据。我们希望人工智能可以从庞大的自然界自动去学习,无监督学习,成为了当前最有前景的研究领域。Ian Goodfellow在2014年提出生成对抗网络后,该领域越来越火,近年来研究最火热的一个领域之一。
1.2 国内外研究现状
近年来,深度学习正在取得重大进展,解决了人工智能界的尽最大努力很多年仍没有进展的问题。它已经被证明,它能够擅长发现高维数据中的复杂结构,因此它能够被应用于科学、商业和政府等领域。除了在图像识别、语音识别等领域打破了纪录,它还在另外的领域击败了其他机器学习技术,包括预测潜在的药物分子的活性、分析粒子加速器数据、重建大脑回路、预测在非编码DNA突变对基因表达和疾病的影响。更令人惊讶的是,深度学习在自然语言理解的各项任务中产生了非常可喜的成果,特别是主题分类、情感分析、自动问答和语言翻译。我们认为,在不久的将来,深度学习将会取得更多的成功,因为它需要很少的手工工程,它可以很容易受益于可用计算能力和数据量的增加。目前正在为深度神经网络开发的新的学习算法和架构更加会加速这一进程。
1.3 研究的基本内容
聚类算法分为划分聚类、层次聚类、密度聚类等,本文采用了其中一些常见,常用的算法进行了介绍。
传统的图像分割方法存在着不足,不能满足人们的要求,为进一步的图像分析和理解带来了困难。第二章将改进的K-均值理论应用在图像分割中,K-均值理论在图像分割中具有很高的应用价值。第三章为了实现准确的电价区域划分,引入模拟人类视觉系统的尺度空间层次聚类算法,提出了一种新的电价区域划分方法。在第四章中,传统的人脸识别方法可分为两类,一种是基于人脸几何特征的,另一种是基于模板匹配的。在第四章中讲述了是基于模糊聚类的人脸分类。
第2章 基于K-均值聚类的图像分割算法
2.1 K-均值聚类算法
K-均值算法是机器学习领域内比较常用的算法之一:先随机地抽取K个对象作为最初的聚类中心。然后计算得出所有对象与各个种子聚类中心之间的距离,再把每个对象指派给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了,每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个:
(1)没有(或最小数目)对象被重新分配给不同的聚类。
(2)没有(或最小数目)聚类中心再发生变化。
(3)误差平方和局部最小。
将样本集划分成k个类,这种划分使得下式最小
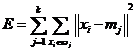 (2.1)
(2.1)
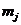 是第j个类的质心,如果想要设计一个算法求得全局最优解,就必须完成C(n,k) 次聚类,找出其中使得E最小的聚类结果。而K均值聚类则是一个求得局部最优解的算法。
是第j个类的质心,如果想要设计一个算法求得全局最优解,就必须完成C(n,k) 次聚类,找出其中使得E最小的聚类结果。而K均值聚类则是一个求得局部最优解的算法。
采用欧氏距离进行距离测量,在n维空间中欧氏距离的公式是:
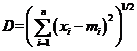 (2.2)
(2.2)
K-均值聚类算法描述
(1)从n个样本中选择k个质心;
(2)将数据集当中每一个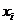 分配到与之相距最近的质心
分配到与之相距最近的质心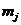 代表的聚类中;
代表的聚类中;
(3)分配后,质心会发生变化,计算新质心以及E值;
(4)重复(2)和(3)直到达到最大迭代次数或新计算的E值与上一次迭代得到的E值之间的差别小于一个给定的阈值。
2.2 基于K-均值聚类的彩色图像分割算法及改进
在图像分割中,K-均值聚类算法得到了广泛应用[1][2]。K-均值聚类算法中,传统的优化算法主要针对聚类数和聚类中心的选取[1][3][2][4],即通过一些聚类有效性的检测函数计算最佳聚类数k ,并在此基础上优化分割效果。近年来,一些研究表明,融合多种图像特征更有利于获得较好的分割效果[3][5][4][6],在对自然彩色图像进行分割中考虑了像素的空间特征,算法有相对较好的鲁棒性。
2.2.1 图像特征提取
颜色特征是图像分割中应用最广泛的视觉特征。在该彩色图像分割算法中,我们采用了LAB颜色模型。在实验室模式中,图像的亮度和颜色信息被分开保存,并且当调整颜色通道时,亮度通道将保持不变。这样,L通道可以被看作是图像的灰度级,它保留了图像的细节,因此很容易通过L通道区分自然和暗图像的细节。此外,LAB模型具有很宽的色域,不仅包含RGB的所有色域,而且弥补了RGB颜色模型中颜色分布的不均匀性。
纹理通常是指在图像中反复出现的局部图案和它们的排列规则[7],具有不依赖于颜色或照度并且可以反映图像中同质现象的特点,本文基于图像的灰度共生矩阵提取图像的纹理特征。根据共生矩阵,可以计算熵、对比度、能量、相关、方差等16种用于提取图像中纹理信息的特征统计量。本文选择了对比度、能量、相关性、同质性描述图像的纹理特征 。特征提取步骤如下:
(1)将彩色图像降为低阶灰度图像,灰度级取为8;
(2)设置出半径d大小为(2d 1)×(2d 1)的窗口化矩阵,按照遍历图像的方法计算得出窗口内灰度共生矩阵,再将其映射到窗口中心所表示的像素上;
(3)基于灰度共生矩阵,利用式(2.3)一式(2.6)计算对比度、能量、相关性和同质性四个纹理特征,并将值返还至对应的像素中心
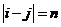
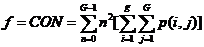 (2.3)
(2.3)
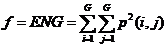 (2.4)
(2.4)
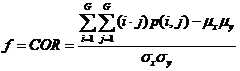 (2.5)
(2.5)
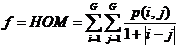 (2.6)
(2.6)
对比度(CON)可认为是图像的清晰度;能量(ENG)则是图像灰度分布的均匀性度量,图像如若呈现较粗的纹理,相应取值较大能量;相关度(COR)是灰度线形关系的度量,是某种灰度值沿着特定方向的延伸长度的反映;同质性(HOM)是图像局部灰度均匀性的度量,假如图像局部的灰度均匀,那么会得到较大的而同质性的取值。另外,考虑到特征值同参与计算的像素的相互联系,针对在图像边缘无法取得完整的窗口信息而无法获取纹理特征值的问题,该章节采取了区域均值的算法,以半径d:3的窗口矩阵为例,边缘像素的值近似会以与其相关的所有纹理特征值之平均值来表示。即:
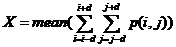 (2.7)
(2.7)
其中(i,j)为x的空间坐标。
2.2.2 K-均值聚类图像分割算法的研究与改进
K-均值聚类算法也称C-均值聚类算法,其基本思想大致是:先随机地抽取K个样本作为最初的聚类中心,计算得出所有样本与各个种子聚类中心之间的距离,把样本指派到与它的距离最近的那个聚类中心所在的类,然后为调整后的新类算出新的聚类中心。如果相邻两次的聚类中心完全一致的话,此次样本调整结束,聚类准则函数已经收敛。
初始聚类中心的选取是K-均值聚类算法中重要的一步,通常是随机选取待聚类样本集的K个样本,聚类的性能与初始聚类中心的选取有关,聚类的结果与样本的位置有极大的相关性。一旦这K个样本选取不得当,运算的复杂程度将会大大增加,使聚类过程出现偏差,令聚类结果不尽人意。采用粗糙集理论为K-均值聚类提供所需要的初始类的个数和均值,提高了聚类的效率和分类的精度。
像素的灰度值为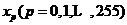 ,其中
,其中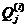 为第 i次迭代后赋给类j的像素集合,
为第 i次迭代后赋给类j的像素集合, 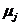 为第j类的均值。具体步骤如下:
为第j类的均值。具体步骤如下:
(1)将粗糙集理论提供的L个中心点P作为初始类均值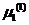 ,
,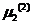 ,
,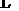 ,
,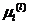 ;
;
(2)在第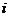 次迭代时,考察每个像素,计算它与每个灰度级的均值之间的间距,即它与聚类中心的距离D,将每个像素赋均值距其最近的类,即
次迭代时,考察每个像素,计算它与每个灰度级的均值之间的间距,即它与聚类中心的距离D,将每个像素赋均值距其最近的类,即
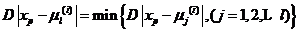 (2.8)
(2.8)
则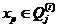 ;
;
(3)对于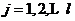 ,计算新的聚类中心,更新类均值:
,计算新的聚类中心,更新类均值: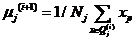 ,式中,
,式中,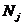 是
是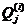 中的像素个数;
中的像素个数;
(4)将所有像素逐个考察,如果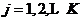 ,有
,有 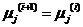 ,则算法收敛,结束;否则返回(2)继续下一次迭代;
,则算法收敛,结束;否则返回(2)继续下一次迭代;
(5)以上步骤结束后,分割结果各类最终灰度用聚类中心灰度值以取得良好的显示。
2.2.3 实验结果与分析

(1)原始图像 (2)K-均值分割后的图像 (3)改进的K-均值分割后的图像
图2.1 图像处理结果
实验表明,基于K-均值聚类算法和粗糙集理论的图像分割方法,对比随机选取聚类的中心点和个数而言,运算量相对减少,分类精度和准确性也得到了提高,同时,在处理低对比度、多层次变化背景的图像时具有轮廓清晰、算法运行速度快、内存占用小等特点,属于相对有效的一种灰度图像分割算法。
第3章 基于尺度空间层次聚类的电价区域划分
3.1 层次聚类分析算法
层次聚类算法[8],又称树聚类算法,其目标是对于具有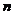 个样本的集合
个样本的集合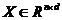 ,先使用相似性函数将样本间的相似性计算出来,从而构成相似性矩阵
,先使用相似性函数将样本间的相似性计算出来,从而构成相似性矩阵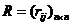 ,再根据该相似性矩阵把样本集构造成一个分层结构,生成一个从1到
,再根据该相似性矩阵把样本集构造成一个分层结构,生成一个从1到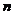 的聚类序列。这个着二叉树的形式的序列,每个树的结点都有两个分支,这会使得聚类结果形成样本集
的聚类序列。这个着二叉树的形式的序列,每个树的结点都有两个分支,这会使得聚类结果形成样本集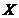 的系统树图
的系统树图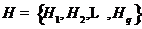 ,
, 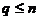 使得
使得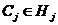
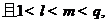 有
有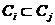 或
或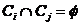 对所有的
对所有的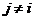 都成立。从系统树图形成的方式来看,层次聚类算法包含两种形式:凝聚式算法和分裂式算法。凝聚式算法是以“自底向上”的方式进行的。首先将每个样本作为一个聚类,然后合并相似性最大的聚类为一个大的聚类,直到所有的聚类都被融合成一个大的聚类。它以
都成立。从系统树图形成的方式来看,层次聚类算法包含两种形式:凝聚式算法和分裂式算法。凝聚式算法是以“自底向上”的方式进行的。首先将每个样本作为一个聚类,然后合并相似性最大的聚类为一个大的聚类,直到所有的聚类都被融合成一个大的聚类。它以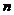 个聚类开始,以1个聚类结束,分裂式算法是以一种“自顶向下”的方式进行的。一开始它将整个样本看做一个大的聚类,然后,在算法进行的过程中考察所有可能的分裂方法把整个聚类分成若干个小的聚类。第1步分成2类,第2步分成3类,这样一直能够进行下去直到最后一步分成
个聚类开始,以1个聚类结束,分裂式算法是以一种“自顶向下”的方式进行的。一开始它将整个样本看做一个大的聚类,然后,在算法进行的过程中考察所有可能的分裂方法把整个聚类分成若干个小的聚类。第1步分成2类,第2步分成3类,这样一直能够进行下去直到最后一步分成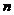 类。在每一步中选择一个使得相异程度最小的分裂。运用这种方法,可以得到一个相反结构的系统树图,它以1个聚类开始,以
类。在每一步中选择一个使得相异程度最小的分裂。运用这种方法,可以得到一个相反结构的系统树图,它以1个聚类开始,以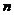 个聚类结束。与分裂式算法相比,由于凝聚式算法在计算上简单、快捷,而且得到相近的最终结果,所以绝大多数层次聚类方法都是凝聚式的,它们只是在聚类的相似性度量的定义上有所不同。
个聚类结束。与分裂式算法相比,由于凝聚式算法在计算上简单、快捷,而且得到相近的最终结果,所以绝大多数层次聚类方法都是凝聚式的,它们只是在聚类的相似性度量的定义上有所不同。
层次聚类算法是一个非常有用的聚类算法,它在迭代的过程中直到所有的数据都属于同一个簇才停止迭代,但是层次聚类也存在几个缺点,如聚类的时空复杂度高、聚类的簇效率底、误差较大等。
3.2 层次聚类分析算法的有效性研究
针对如何从层次聚类算法得到样本集的多种聚类结果中获得用户最满意的聚类结果,在深入研究聚类有效性的基础上,通过模糊相似性关系刻画聚类的类内致密性和类间分离性,可以建立一个聚类的有效性函数。在人工和实际数据集上的实验都表明了该有效性函数具有良好的性能。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: