摘 要

在现如今的机器学习范畴一般用到最多的主要有三大类学习方法：即有监督学习、无监督学习以及半监督学习。BP（Back Propagation）神经网络是一种通过误差反传算法进行机器训练的多层前馈网络。同时也是当今世界上在生产实践中运用最普遍的神经网络模型之一。支持向量机SVM(Support Vector Machine)主要应用于分类领域，在处理诸多模式识别案例时都展示出了其独特的优点。可以运用在其它相关的机器学习范畴。在统计学领域中，线性回归是通过回归方程的最小二乘函数来演算一个或多个输入值与输出值之间的关系的回归问题分析。

本文首先介绍了神经网络算法中的BP神经网络算法分析了它的计算原理以及结构并重点介绍了BP网络的训练过程以及设计BP网络过程中的几个必不可少的影响因素。其次介绍了支持向量机算法，通过原理图详细的叙述了支持向量机算法的基本原理以及几个基本的概念。重点介绍了SVM算法中关于最优分类器的问题以及数据归一化原理。分析了SVM算法的特点以及不足之处与其鲁棒性特征。最后本文介绍了线性回归算法，重点以一元线性回归算法为例分析了线性回归的基本原理与运用领域及其特点，对多元线性回归也进行了一定的分析。同时本文通过上述三种算法对肌肉电信号数据库进行了Matlab仿真最后得出结论：神经网络算法能模仿人类大脑神经元组织进行运算，泛化性强；支持向量机一般适用于离散型样本的分类，而线性回归算法则一般适用于具有较强线性规律的连续样本。

中文关键词：有监督学习；人工神经网络；支持向量机；线性回归

Abstract

There are three main types of learning methods we use the most in the field of machine learning nowadays: supervised learning, unsupervised learning and semi-supervised learning. BP （Back Propagation） neural network is a multi - layer feedforward network for machine training by error - back algorithm. It is also one of the most common neural network models used in production practice in the world. SVM (Support Vector Machine) is mainly used in classification field, and it has shown its unique advantages when dealing with many pattern recognition cases. It can be used in other related areas of machine learning. In the field of statistics, linear regression is the regression problem analysis of the relationship between one or more input values and output values through the least square function of regression equation.

This thesis first introduces the BP neural network algorithm in the neural network algorithm analyses its principle and the structure and focus on the training process of BP network, and design several essential factors in the process of BP network. Secondly, the algorithm of SVM is introduced, and the basic principle and several basic concepts of SVM algorithm are described in detail through the schematic diagram. The problem of optimal classifier in SVM algorithm and the principle of data normalization are introduced. The characteristics, shortcomings and robustness of SVM algorithm are analyzed. Finally linear regression algorithm is introduced, the key to a yuan linear regression algorithm as example analyzes the basic principle and application field and the characteristics of linear regression, the multiple linear regression and was analyzed. At the same time, the above three algorithms are used to simulate the muscle electrical signal database with Matlab. Finally, the conclusion is drawn that the neural network algorithm can simulate the human brain neuron tissue to carry out the operation generalization is good, support vector machine generally applied to discrete sample classification, and linear regression algorithm is generally applicable to continuous sample has strong linear rule.

Key Words: supervised learning; artificial neural network; support vector machine; linear regression

目录

第1章 绪论 1

1.1 课题背景及目的 1

1.2 国内外研究背景及发展 1

1.3 本文研究内容与结构 2

第2章 神经网络 3

2.1 概述 3

2.2 基本思想 3

2.3 BP神经网络训练过程 4

2.4 BP神经网络的设计 5

2.5 BP网络实现 6

第3章 支持向量机 7

3.1 概述 7

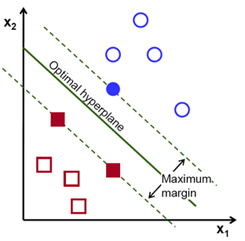
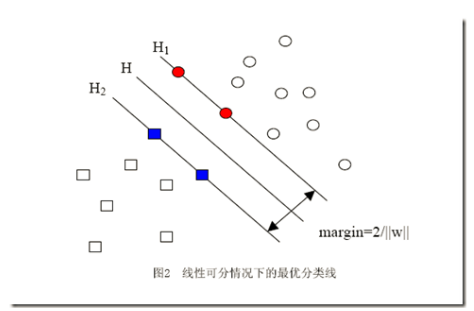
3.2 SVM的基本原理 7

3.3 寻找最优分类器 10

3.4 归一化 10

3.5 SVM的优缺点 11

第4章 线性回归 13

4.1 概述 13

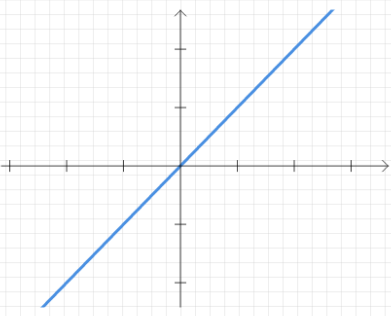
4.2 一元线性回归 14

4.3 多元线性回归 16

第5章 Matlab仿真结果及分析 17

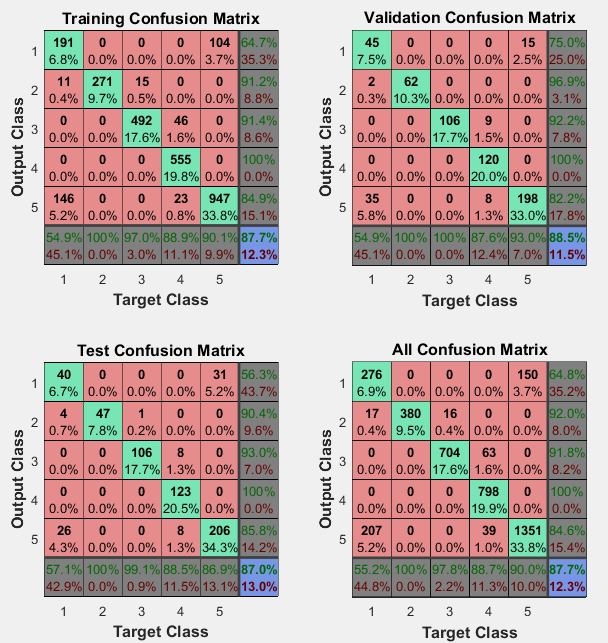
5.1 神经网络仿真 17

5.2 支持向量机仿真 18

5.3 线性回归仿真 18

第6章 结论 20

参考文献 22

致谢 23

第1章 绪论

1.1 课题背景及目的

在现如今的机器学习范畴业界用的最多的主要有三大类学习方法：即有监督学习、无监督学习以及半监督学习。

而在这三大类学习方法中，有监督学习是应用最普遍最具代表性的机器学习方法。系统能够通过它从诸多训练数据中模仿乃至建立新的学习模型，并推测这种模式中的新实例。训练数据由输入矢量和预期输出矢量构成。函数的输出结果可以是一个预测的分类标记也可以是一个连续的有理数值。可以简单的来说，有监督学习算法是先给定一组输入x和输出y的训练集，而后让系统学习如何将输入x和输出y关联起来。在大多数情况下，这里的输出结果y是很难自动收集的，所以说这里就需要人来提供某种意义上的“监督”^[1]。不过除此之外有监督学习这个术语依然可以适用于训练集目标能够被系统自动收集的案例^[2]。总的来说，有监督学习实质上可以归类于应用统计学^[3]。在本篇论文中本人将对神经网络算法，支持向量机算法以及线性回归算法进行研究学习。

1.2 国内外研究背景及发展

自从科学、技术与人工智能的基本观点诞生时起科学家们便跟随着Blaise Pascal和Von Leibniz的脚步思考是否有一种机器能拥有与人类相同的智能^[4]。著名作家如Jules Verne，Frank Baum(绿野仙踪)，Marry Shelly(弗兰肯斯坦)，George Lucas(星球大战)等幻想着人造人有着与人类相似甚至更强的能力。机器学习(Machine Learning)是人工智能非常热门的一个方向，无论是在学术界还是工业界，企业和大学等机构都投入了大量的资源来提升他们在这方面的研究力度，并在此领域的很多项目中取得了实实在在的成果^[5]。回看历史，向着机器学习前进的第一步是由Hebb在1949年迈出的，基于一个神经心理学的学习公式它被称为Hebbian学习原理^[6]。简单来讲它加深了节点和递归神经网络的相关性。它记住了所有网络的共性并在之后能使其如同人的大脑一般工作。概况地来说关于它的论述如下：当一个神经细胞A的轴突足够接近来使细胞B兴奋或持续地保持激活状态时，一些增长过程或新陈代谢的变化会在其中一个或双方细胞之间发生，这样的话A的工作效率在刺激B的同时会升高。在1952年，Arthur Samuel在IBM研发出了会下跳棋的程序^[7]。该程序能够观察棋子的位置，并学习得出一个模糊的模型与此同时指导其为之后的步骤做出更好的决策。Samuel与程序下了很多次棋并发现程序能够随着时间的推移而下的越来越好。于是Samuel借此反驳了公众关于机器执行的命令不能够超越所写代码并如人类一般学习的认知。也正是他创造了机器学习(machine learning)这一术语。机器学习的一大重要突破来源于支持向量机由Vapnik 和 Cortes于1995年在非常有力的理论依据和经验结果下得出^[8]。正是这时机器学习社区分为了神经网络和支持向量机两大拥护群体。然而对于神经网络的支持者来说当Kernelized于2000年提出新版本SVM理论后竞争的优势并不在他们这边。SVM在原来许多神经网络成功的案例中都取得了更好的成绩。同时SVM也能够利用所有之前的凸优化广义边际理论和核心理论来对抗NN模型^[9]。因此SVM能够在不同的领域都取得重大理论和实践的发展。当时间逐渐来到二十世纪，一个神经网络的新时代即深度学习^[10]诞生了。而神经网络的第三次崛起大概是在2005年，经过多年的发展之后神经网络模型拥有了完成许多任务的能力如物体识别^[11]，演讲识别，自然语言处理等，这使得深度学习成为时代的佼佼者。然而要强调的是这并不代表着其他机器学习流派的终结。虽然深度学习的成功案例越来越多，但仍存在很多批评的声音指向神经模型的训练代价过大和对外源参数的调整能力欠佳这两个不足之处。而与此同时SVM仍然凭借其简易性至今仍在被广泛运用。

1.3 本文研究内容与结构

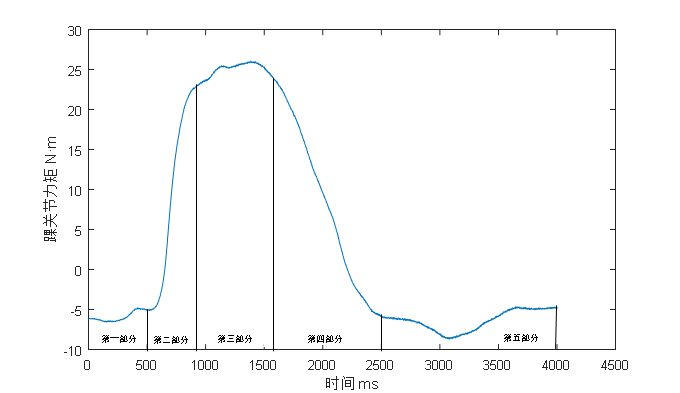
本文主要研究学习了几种典型的有监督学习算法即神经网络算法，支持向量机算法与线性回归算法。分析每一种算法的实现原理，运用领域以及各自的特点。在第一章绪论内容中本人首先简要介绍了本论文的研究对象以及关于机器学习理论的发展及研究背景。在第二章中本人介绍了神经网络算法中的BP神经网络算法分析了它的计算原理以及结构并重点介绍了BP网络的训练过程以及设计BP网络过程中的几个必不可少的影响因素。在第三章中本人介绍了支持向量机算法，通过原理图详细的叙述了支持向量机算法的基本原理以及几个基本的概念。随后重点介绍了SVM算法中的核心问题及关于最优分类器的确定问题同时也介绍了在数据预处理时的归一化原理。最后分析了SVM算法的特点以及不足之处与其鲁棒性特征。在第四章中本人介绍了线性回归算法，重点以一元线性回归算法为例分析了线性回归的基本原理与运用领域及其特点。同时对多元线性回归也进行了相应的介绍对其原理做了一定程度的分析与阐释。在第五章本人通过上述三种算法对实验采集的一组肌肉电信号数据库进行了Matlab仿真并对仿真结果进行了分析。最后一章总结部分本人结合了现阶段对机器学习的认识和本论文的研究对象阐述了论文心得，在总结自己不足之处的同时对未来进行了展望。

第2章 神经网络

2.1 概述

BP（反向传播）神经网络是由RunelHART和McCeland领导的研究小组于1986年在《自然》杂志上提出的概念。

这是一种通过误差反传算法进行机器训练的多层前馈网络。同时也是当今世界上在生产实践中运用最普遍的神经网络模型之一。BP网络可以在不用预先描述映射的数学方程的条件下学习存储大量的输入输出模式的映射关系。它的学习原理是使用最速下降法来实现最小化网络的误差方差。首先本文可以简要介绍一下生物神经元网络。神经网络顾名思义，其灵感当然来自于自然界已存在的生物神经元网络。在生物学中，一个神经元由树突，轴突以及细胞体三大部分组成。其中树突是神经元的信号输入部分，它会接受来自其它神经元对它产生的激励信号。轴突是神经元的输出部分，它将神经元产生的激励信号作用于其它神经元的树突。细胞体是神经元的主体部分。它会对来自其它神经元传来的激励信号产生相应的生理作用同时决定神经元的激励或是抑制状态。而生物神经元系统是由许许多多神经元经过及其广泛而有效的连接构成的复杂系统。

2.2 基本思想

误差的反传以及有用信号的正传是BP神经网络的两个基本学习过程。

（1）当信号正传时，输入层发送输入样本。在通过隐藏层计算后发送到输出层。如果输出层的实际输出相比较期望的输出信号有较大出入。信号将会被送回到误差的反传阶段。（2）当误差反传时，输出会经过隐层送回到输入层。并将其分配给每个层的各个单元。从而得到其各自的误差信号即修改各层权值的基础。信号流程图如下:

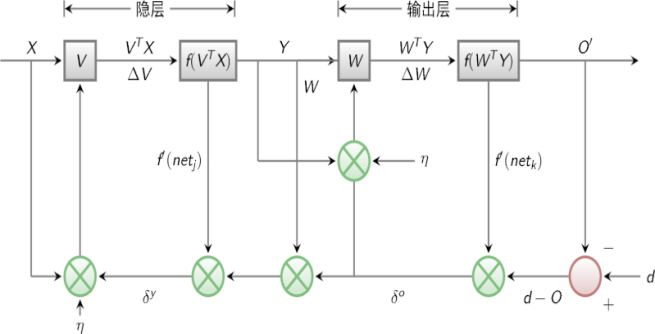
图2.1 误差反传信号流程图

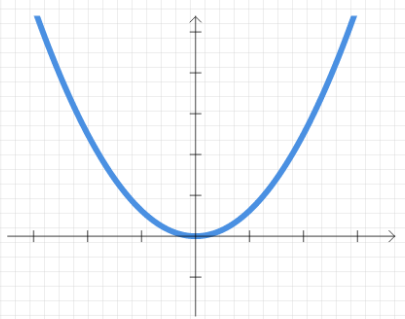
BP网络中的传递函数S函数（如图2.2）是一种非线性函数。S函数原函数及其导数在其定义域内都是连续的因此很适合运用于计算机的算法领域。

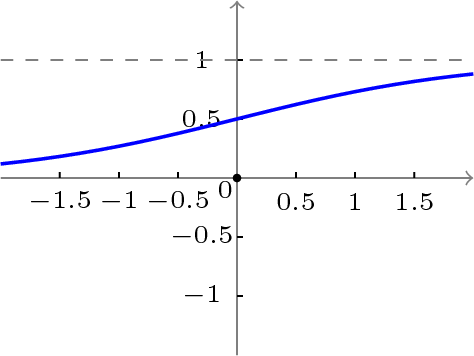
图2.2 S函数图像

2.3 BP神经网络训练过程

前向传输：在训练网络之前，偏差以及权重的初始化我们都是随机处理的。即每个偏差和每个权重都是我们随机选取的一个实数，然后进行前向传输。第一步，确定输入层的输出值。倘若属性的数量为n，则输入层的神经单元数也必须为n。与此同时输入层的节点数与属性值的维度相同。每个节点的输出值都是由节点的输入值通过计算得到的。所有层的输入值都是由节点之前的输入数据与偏置权重相加的运算结果。当然上述步骤不适用于输入层。

逆向反馈：顾名思义，逆向传输就是从输出层末端开始。首先需要明白的一点那就是输出层所输出的结果类别通常就是人们进行神经网络训练的最终目的。对于一种最常见的二分类问题而言通常会在输出层的最后一层设置两个神经元输出节点。通过比较两个神经元输出值的大小来将计算结果分类，即可以定义倘若神经元一的输出值小于神经元二的输出值则可定义为分类一。反过来如果神经元一的输出值大于神经元二的输出值则可定义为分类二。由于整个网络的权值以及偏差都是系统自定的随机值。仅靠神经元的输出还不足以描述记录的分类。因此偏置与权重基于误差都需要重新定义。与此同时神经网络通过不断减小输出层与实际类别的误差从而达到优化效果。拿二分类问题举一个例子。假设用10等价分类1,11等价分类2。对于数据类别1的输出层结果而言它的隐层值是通过其下层所有输入节点的误差按权重的累加计算而来的。而不是与数据记录结果产生直接的关系。终止条件主要有以下两种：1.确定一个最大迭代次数，例如当数据集迭代完成1000次后训练终止。2.设置训练集在训练时的预测误差率，低于设定的门限值时终止训练。

2.4 BP神经网络的设计

在BP网络的设计中。重要的影响因素主要有：初始值、各层神经元数目、学习速率等。以下是一些设计原则：

网络层数：理论上，任何一个有理函数都可以由S函数的非线性隐层和一个线性输出层串联来表示。我们当然可以通过增加隐层来提高精准度。但与此同时系统也变得更加复杂了。与此同时，我们往往也不能靠只具有非线性的激活函数单层系统来完成计算。因为自适应线性网络几乎可以覆盖单层非线性的所有功能。而且在大多数情况下自适应线性网络的计算效率是远高于非线性网络的。所以说，对于只能使用非线性网络的系统而言。增加网络层数是达到预期效果的唯一途径。而且系统的计算精度低运行速度慢。

隐层神经元个数：要想提升网络计算精确程度的方法有很多。其中增加网络层数的方法虽然可行但过程十分冗杂。而增加隐层神经元数就简单很多了。在大多数情况下，训练网络精度的时间就是衡量网络质量的标准。（1）神经元数量偏少时。网络学习不好。训练次数增多。训练精度低。（2）神经元数量偏多时。网络函数强。精度越高，训练次数越多。但可能会出现过拟合现象。

由上可知，隐层神经元个数的确定准则是：如果现有网络结构足以解决问题。再原有基础上再加上一两个隐层神经元。能起到让误差迅速降低的效果即可

初始权值的选取：大多数情况下是在(−1,1)之间随机产生。威得罗等人基于两层网络函数的训练过程提出了著名的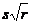的策略。其中s为第一层神经元个数。r为输入个数。

学习速率：学习率的普遍取值在0.01～0.8之间。高学习率会降低系统的稳定性。而过低的学习速率会严重影响收敛的速度。这需要较长的训练时间。而对于较复杂的网络该怎么处理呢？这时我们可以将不同的学习速率运用到误差曲面的不同位置。即自适应学习速率。使用自适应学习速率是减少寻找学习速率时间和训练次数的普遍方法。即在网络在各个阶段设定与之相匹配的学习速率。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：