涡旋光束轨道角动量的模拟与分析毕业论文
2020-04-10 16:16:33
摘 要
涡旋光束因具有一个附加的螺旋相位因子,从而获得了螺旋形的等相位面结构,并且携带的轨道角动量在拓扑荷数发生变化时也会出现差别。由于这一特性,导致涡旋光束在粒子微操纵、非线性光学、光通信等领域有着非常普遍的应用。
本次研究主要包含了涡旋光束的基本性质、其轨道角动量的理论计算以及分析其拓扑荷数的影响(通过干涉原理)三个方面。首先,对涡旋光束的研究背景及现状进行了介绍,表明了本次研究的目的。然后阐述了涡旋光束的基本原理,还分析了其波印廷矢量,介绍了涡旋光束的几种产生方法的相关原理——光学仪器转换法、计算全息图法、螺旋相位板法,同时分析了其利弊,并举例说明了涡旋光束的几种常见类型。其次,在轨道角动量这一章中,分别对线偏振和圆偏振模式下的轨道角动量进行了理论计算,得出了涡旋光束的一些基本特性。最后,本文介绍了如何通过干涉原理测量出涡旋光束的拓扑荷数,借助了计算机软件绘制出平面波与涡旋光束的干涉图样、球面波与涡旋光束的干涉图样,然后得出了可以通过观测涡旋光束的干涉图样来获取其拓扑荷数的结论。
关键词:涡旋光束;轨道角动量;拉盖尔-高斯光束;拓扑荷数
Abstract
The vortex beam with an additional helical phase factor obtain equiphase surface structure of the spiral, and when the topological charge number is not at the same time, the orbital angular momentum of vortex beam itself also can appear difference. Because of this characteristic, vortex beam is widely used in particle micro-control, nonlinear optics, optical communication and other fields.
This study mainly includes the basic properties of vortex beam, the calculation of orbit angular momentum of vortex beam and the analysis of topological charge of vortex beam by interference principle. First of all, we introduce the background and current situation of the study of vortex beam, which indicates the purpose of this study. Then expounds the basic principle of vortex beam, also analyses the Poynting vector, this paper introduces the methods of several kinds of vortex beam optics transformation method, the calculation method of hologram, the related principle of spiral phase plate method, and analyzes its advantages and disadvantages and several common types of vortex beam is illustrated by an example. Second, the vortex beam of orbital angular momentum in this chapter, respectively for linear polarization and orbital angular momentum of the circular polarization mode has carried on the theoretical calculation, some basic characteristics of the vortex beam is obtained. Finally, this paper introduces the principle how to through the interference measure the topological charge of vortex beam, we use the computer software to map the plane wave and vortex beam interference pattern, spherical wave and vortex beam interference pattern, and then obtained could be obtained by observation of vortex beam interference pattern the conclusion of the topological charge number.
Key words: vortex beam; Orbital angular momentum; Laguerre-Gaussian beams; the topological charge number
目录
摘要 Ⅰ
Abstract Ⅱ
第1章 绪论 1
1.1 引言 1
1.2 光学涡旋的研究背景及发展现状 1
1.3 涡旋光束的应用 2
1.3.1 粒子捕捉与操控 2
1.3.2 光通信 2
1.4 本文研究意义及内容 3
第2章 涡旋光束的相关理论 4
2.1 涡旋光束的基本原理 4
2.2 涡旋光束的数学描述 4
2.3 涡旋光束的波印廷矢量 6
2.4 产生涡旋光束的办法 8
2.4.1 光学仪器转换法 8
2.4.2 计算全息法 9
2.4.3 螺旋相位板法 9
2.5 几种常见的涡旋光束 10
2.5.1 拉盖尔-高斯光束 12
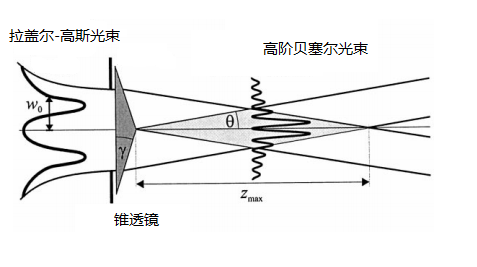
2.5.2 贝塞尔-高斯光束 13
第3章 涡旋光束的轨道角动量 15
3.1 涡旋光束轨道角动量的数学描述 15
3.2 线偏振激光模式的轨道角动量 15
3.3 圆偏振激光模式的轨道角动量 16
第4章 分数阶与整数阶的拉盖尔-高斯光束理论计算 19
4.1 拓扑荷为整数时的光束特性 19
4.1.1 与平面波的干涉 19
4.1.2 与球面波的干涉 20
4.2 拓扑荷为非整数时的光束特性 20
4.2.1 与平面波的干涉 20
4.2.2 与球面波的干涉 21
第5章 结论与展望 22
参考文献 23
致谢 24
第1章 绪论
1.1 引言
光学是物理学的一个重要部分,也是当前科学研究中最活跃的学科之一。在人类探索客观世界的过程中,光学的发展也是其中一个重要的组成。在光学领域,一种独特的光束以其本身固有的特殊性质引起了学术界的高度关注,那就是——涡旋光束(vortex beam)。现在,科学家们对光学涡旋的研究已经成为一个光学前沿热点,其在光学微操纵和信息传输等领域的潜在应用价值也逐渐被开发。
1.2 光学涡旋的研究背景及发展现状
早在十九世纪三十年代,Airy就在实验中发现了透镜的焦平面处有奇怪的光圈 [1]。随着光学研究的不断进展,人们逐渐发现有些光束具有相位奇点[2]。但直到二十世纪九十年代,这些相位奇点的专业术语“光学涡旋”(optical vortices)才被Coullet等人首次引入[3]。早在1970年,Ashkin利用一束光照射微粒,使得粒子处于悬浮状态,这是第一次使用光来对微粒进行捕捉,为光镊技术的研究打开了一扇门[4]。几年后,Ashkin又发现当激光的电磁场分布不均匀时会产生的梯度力,从而影响光辐射压[5],这也是历史上第一次完整得证明了可以通过激光光束来捕获粒子。这些光束可以对粒子进行捕捉获取,其作用类似于生活中的镊子,故称其为光镊技术。随着光镊技术的不断进展,普通光镊已经无法满足人们在操控粒子方面的需求,这时,一种特殊的光源——涡旋光束,开始引起了人们的注意。
1992年,Allen等人证明了在傍轴近似的条件下,具有相位因子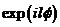 的光束具有
的光束具有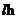 的轨道角动量,即涡旋光束具有确定的轨道角动量[6]。这一结论使得人们对于此类特殊结构光场重视起来,并为后来涡旋光束轨道角动量在应用方面提供了理论依据。1994年,Allen等人再次证明了涡旋光束在非近轴条件下仍具有
的轨道角动量,即涡旋光束具有确定的轨道角动量[6]。这一结论使得人们对于此类特殊结构光场重视起来,并为后来涡旋光束轨道角动量在应用方面提供了理论依据。1994年,Allen等人再次证明了涡旋光束在非近轴条件下仍具有 的轨道角动量[7]。
的轨道角动量[7]。
涡旋光束所具有的轨道角动量决定了这种类型的光束在与物质相互作用的过程中,将自身携带的角动量传递给粒子,引起粒子的角向偏转[8],这一理论于1995年被He等人在实验中证实,并实现了对粒子的控制。1996年,Simpson等人也做了类似的实验,实验发现涡旋光束可以对粒子进行旋转操作,证实了其具有轨道角动量,并将这种技术定义为“光学扳手”[9]。这一发现使涡旋光束的潜在应用价值被人们发现,也恰是涡旋光束在粒子操控的光学领域中的无可取代,使得其一直是人们关注的热点。
自二十一世纪初期以来,我国研究涡旋光束的人也越来越多,人们开始对涡旋光束的产生、传播特性、轨道角动量、光力特性、应用等方面的深入研究。
1.3 涡旋光束的应用
涡旋光束因具有普通高斯光束所没有的各种特性,如光束奇点处光强为零、中心暗斑极小、自身带有轨道角动量等等许多特点,使得其在非常多方面都可以进行应用研究,接下来简要介绍涡旋光束应用的几个热门领域。
1.3.1 粒子捕捉与操控
光对粒子可以有力的作用,又可以看做光子流动时产生的压强,所以称这种作用为光压。当粒子在光学涡旋中受到力的作用大致分为两种情况,一种是在涡旋光束的亮环上,利用聚焦环形光场产生的梯度力,束缚高折射率的小粒子;另一种是在光束的中心暗斑区,利用光场结构,束缚低折射率的粒子。
大家都知道光镊是一种用于捕获粒子十分高效的工具,其原理如图1.1所示。实质上光镊的基本原理就是单光束对粒子进行捕捉形成光阱,但普通的光镊是利用一般的高斯光束进行工作,所以在捕获过程中存在一些问题有待解决。例如通常使用高斯光束光强聚焦的最强区域进行捕获操作,这样很容易对想要捕获的样品产生灼伤,而且不方便进行旋转操作。但是通过涡旋光束进行光镊方面的研究,由于其在涡旋中心光强为零且具有轨道角动量的特点,上述普通光镊存在的问题就迎刃而解了。
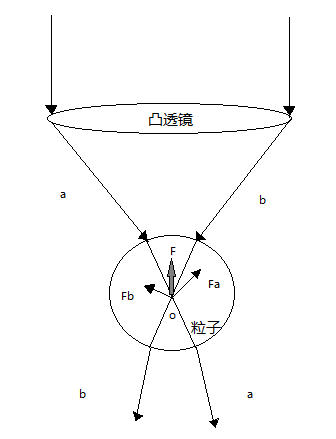
图1.1 几何光学捕获粒子受力示意图
1.3.2 光通信
由于涡旋光束具有在信息传输过程中安全性且可以存储大容量的信息的特点,越来越多的人开始研究其在光通信方面作为传播信息的媒介的应用[10]。接下来介绍一下涡旋光束在光通信领域的应用价值。
首先,传输过程信息的安全性高,只有将信息接收器放置在涡旋光束的传播路径中才能获得信号,即使接收到信号,也很难将传输数据进行完全恢复。
其次,可以通过独特的轨道角动量存储大量信息,一般的高斯光束只拥有2种自旋角动量,所以相当于只能代表二进制中的“0”、“1”,但涡旋光束不仅拥有2种自旋角动量以外还具有确定的轨道角动量,且随着其轨道角动量选取任意值,在传输信息时可以代表任意进制,携带的信息容量也大大提升。
1.4 本文研究意义及内容
由上述描述可知,涡旋光场作为一种特殊的光场,因其对粒子的捕获具有无损伤的特点,且具有较大的捕获效率,在物理、生物学及化学[11-13]等研究领域也具有重要作用。本次研究希望可以为将涡旋光束更好地应用到各个领域提供理论依据。
本文的主要包括以下内容:
- 在第一章中对涡旋光束的研究现状进行总结,并简要介绍了涡旋光束的部分应用。
- 第二章介绍了涡旋光束的基本原理,分析了其波印廷矢量。介绍了涡旋光束的产生方法,分析了其原理及其利弊。然后介绍了几种典型的涡旋光束,对其光强分布进行了理论计算,并通过MATLAB进行仿真。
- 第三章介绍了涡旋光束的轨道角动量,并对在自由空间传播傍轴条件下的涡旋光束进行了理论分析。
- 第四章提出了通过干涉原理来测量涡旋光束的拓扑荷数的方法。借助MATLAB对涡旋光束的干涉图样进行仿真
- 最后在第五章中研究内容进行总结和展望。
第2章 涡旋光束的相关理论
2.1 涡旋光束的基本原理
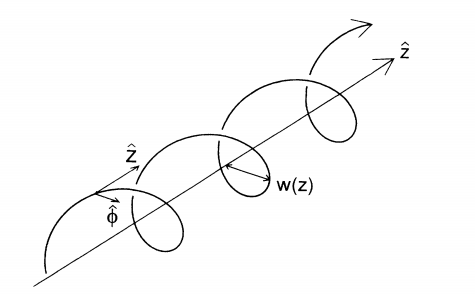
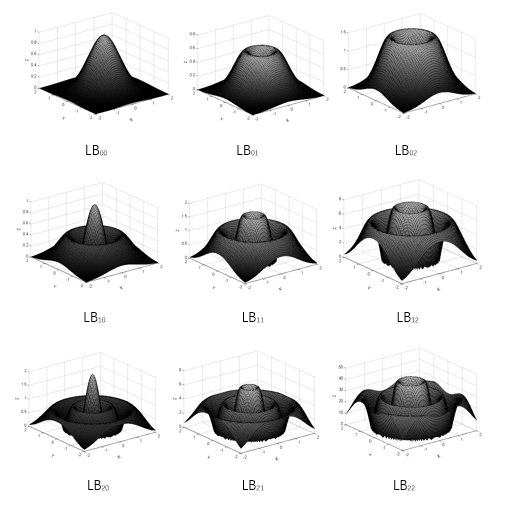
在平面中存在一个类似“晶体缺陷”在晶体中的螺旋缺陷时,光束会绕着传播方向发生旋转,在旋转的过程中,会出现一个绕轴旋转的光波,称其为螺旋波。光波的相位表示的是光的局域传播方向,光波波前(即等相位面)的法线方向与其能流方向一致,这样看来,在光强为零的地方(即相位奇点)可以产生一个光的涡旋,由于其等相位线是螺旋线,称之为光学涡旋(optical vortice)。例如,LG01(拉盖尔-高斯光束)是一个特殊的一阶涡旋光束,具有一个相位奇点,N阶的涡旋光束存在N个相位奇点。
因为涡旋光束的等相位面具有螺旋对称性,所以在光束的传播过程中,中心光强恒为零,也正因为这个螺旋波前,使得涡旋光束具有了轨道角动量。
2.2 涡旋光束的数学描述
涡旋光束的相位部分可以写为: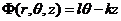 ,其中
,其中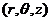 代表的是柱坐标系,z为涡旋光束传播的距离,l为拓扑荷数。同时为了描述光波是沿着z轴方向传播,增加一个相位因子
代表的是柱坐标系,z为涡旋光束传播的距离,l为拓扑荷数。同时为了描述光波是沿着z轴方向传播,增加一个相位因子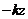 ,其中k为波数,大小为
,其中k为波数,大小为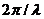 。因此对于一个拓扑荷数为l的涡旋光场,假设其振幅分布函数为
。因此对于一个拓扑荷数为l的涡旋光场,假设其振幅分布函数为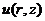 ,可以得出其场强的数学表达式为:
,可以得出其场强的数学表达式为:
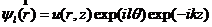 (2.1)
(2.1)
由上式可以看出,场强表达式中含有一个相位因子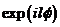 ,这决定了光束的涡旋相位。当拓扑荷数为l的时候,沿螺旋环绕一周,相位相应的发生了
,这决定了光束的涡旋相位。当拓扑荷数为l的时候,沿螺旋环绕一周,相位相应的发生了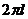 的变化,从而形成了沿传播方向前进的涡旋波前。在涡旋光束的中心相位是不确定,且中心的光强为零。
的变化,从而形成了沿传播方向前进的涡旋波前。在涡旋光束的中心相位是不确定,且中心的光强为零。
图2.1,2.2是在不同拓扑荷数情况下的涡旋光束的二维、三维的等相位分布图。
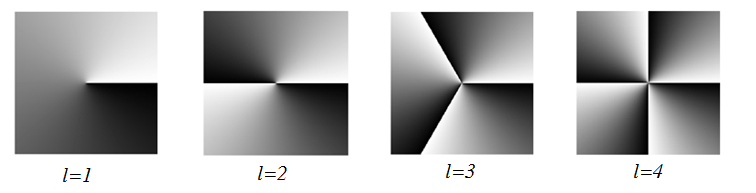
图2.1 不同拓扑荷数的涡旋光束的二维等相位面图
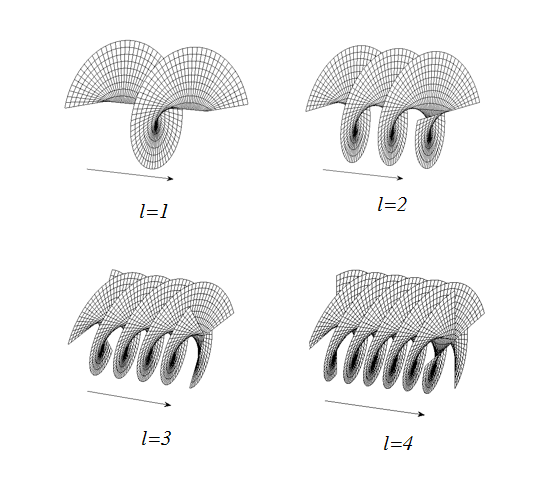
图2.2 不同拓扑荷数的涡旋光束的三维等相位分布图
涡旋光束最主要的特点之一是它们在空间传播时能保持其特征不变。图2.3绘制的是一个涡旋光束在空间中传输过程的光强对比图,可以很容易地得出即使在传播过程中有很大的不确定性,但光强分布中心的暗孔还是被保留下来了的结论。

图2.3 涡旋光束传播到一定距离时的光强
2.3 涡旋光束的波印廷矢量
波印廷矢量是为了描述能量在场内的传播所引入的能流密度,它在数值上等于在单位时间流过单位横截面的能量,通常用符号S表示它[14]。波印廷矢量是涡旋光束非常重要的性质之一,可以通过研究波印廷矢量的分布变化的方法来推导涡旋场内能量的变化。
接下来以拉盖尔-高斯光束为例,研究波印廷矢量的性质。拉盖尔-高斯光束复振幅的表达式为[14]
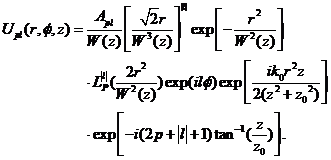 (2.2)
(2.2)
其中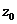 是高斯光束的瑞利长度,
是高斯光束的瑞利长度,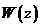 是其光斑半径,
是其光斑半径,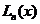 为n阶的拉盖尔多项式。对于除基模外的拉盖尔-高斯光束,振幅表达式中相位表示了其波前相位的螺旋状,由此产生的轴向相位不连续与这些模式的z=0时强度一致。同时相位表面的螺旋性表明光波的波面与z轴并不垂直,因此波印廷矢量与传播方向不平行。对于线偏振模式下的拉盖尔-高斯光束,波印廷矢量为
为n阶的拉盖尔多项式。对于除基模外的拉盖尔-高斯光束,振幅表达式中相位表示了其波前相位的螺旋状,由此产生的轴向相位不连续与这些模式的z=0时强度一致。同时相位表面的螺旋性表明光波的波面与z轴并不垂直,因此波印廷矢量与传播方向不平行。对于线偏振模式下的拉盖尔-高斯光束,波印廷矢量为
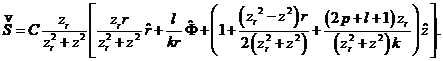 (2.3)
(2.3)
式中的C是一个只取决于强度分布径向位置的常数。如果忽略上式中的小量,则波印廷矢量被简化为
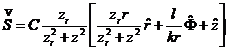 , (2.4)
, (2.4)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: