热冲击载荷作用下超高温陶瓷复合材料的热力耦合分析毕业论文
2020-02-18 10:05:32
摘 要
超高温陶瓷复合材料因为其较高的熔点和较好的抗氧化烧蚀性能,所以得到了广泛的关注。但是由于超高温陶瓷复合材料是一种典型的脆性材料,在极端加热的条件下很容易发生热冲击失效,产生严重的后果,所以需要对超高温陶瓷复合材料抗热冲击性能进行。因此,本文使用基于态的近场动力学理论模拟了超高温陶瓷复合材料在热冲击载荷作用下的热力耦合分析。本文总结了基于态的近场动力学的热力耦合理论,并将其离散化。在此基础上设计了计算流程,同时利用Fortran程序设计语言编写了相应的计算程序。计算得到结果,并对其进行分析。
关键词:近场动力学;热力耦合;超高温陶瓷复合材料;热冲击
Abstract
Because of its high melting point and good resistance to oxidation and ablation, ultra high temperature ceramic composites have attracted extensive attention.However, as ultra-high temperature ceramic composite is a typical brittle material, it is easy to have thermal shock failure under extreme heating conditions, resulting in serious consequences. Therefore, it is necessary to study the thermal shock resistance of ultra-high temperature ceramic composite.Therefore, this paper simulates the thermodynamic coupling analysis of ultra-high temperature ceramic composites under thermal impact load by using the near field dynamics theory based on state.In this paper, the thermodynamic coupling theory based on state near field dynamics is summarized and discretized.At the same time, the Fortran programming language is used to write the corresponding program.The results are calculated and analyzed.
Key Words:peridynamics;Thermal coupling;Ultra high temperature ceramic composites;Thermal shock
目录
第1章 绪论 1
1.1 研究背景 1
1.2 超高温陶瓷复合材料的抗热冲击研究现状 1
1.3 近场动力学的研究现状 2
1.4 本文主要研究内容 3
第3章 近场动力学理论 4
2.1 近场动力学 4
2.1.1 基于键的近场动力学 4
2.1.2 基于键的近场动力学的瞬态热传导方程 5
2.1.3基于键的近场动力学的热力耦合方程 6
2.2 基于态的近场动力学热力耦合理论 6
2.2.1 基于态的近场动力学的运动平衡方程 6
2.2.2 基于态的近场动力学的热力耦合方程 7
2.3 本构方程的更新 8
2.3.1 陶瓷材料的本构方程 8
2.3.2 Ti金属的本构方程及其相关参数 10
2.3.3 复合材料的本构方程及参数确定 11
2.4 本章小结 12
第3章 近场动力学模型的数值离散及程序实现 13
3.1 近场动力学理论的离散化 13
3.2 热力耦合分析中的边界问题 13
3.2.1 瞬态热传导问题的边界处理 13
3.2.2 位移边界问题的处理 14
3.3 速度verlet算法 14
3.4 程序的实现及程序流程图 15
3.4.1程序的设计 15
3.4.2程序流程图 16
第4章程序的数值结果及分析 19
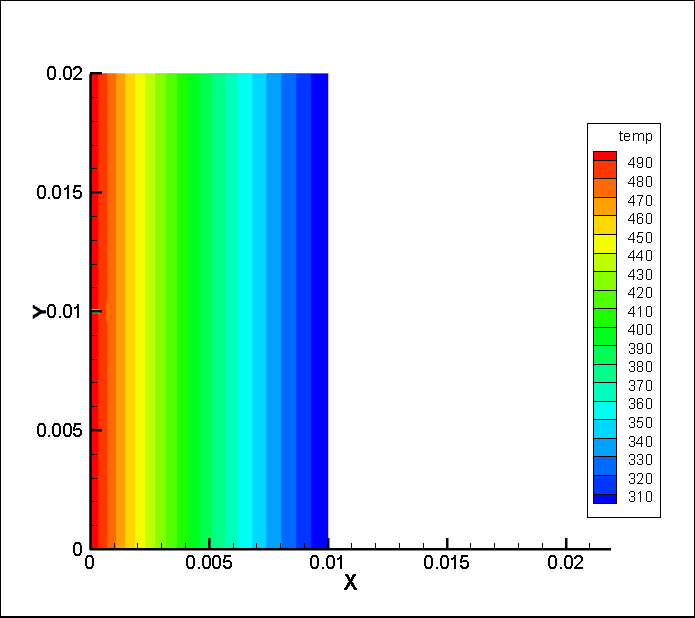
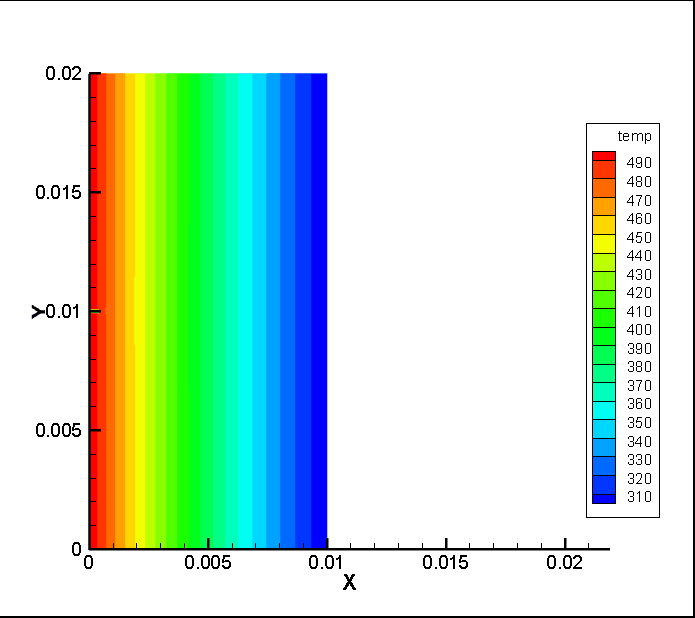
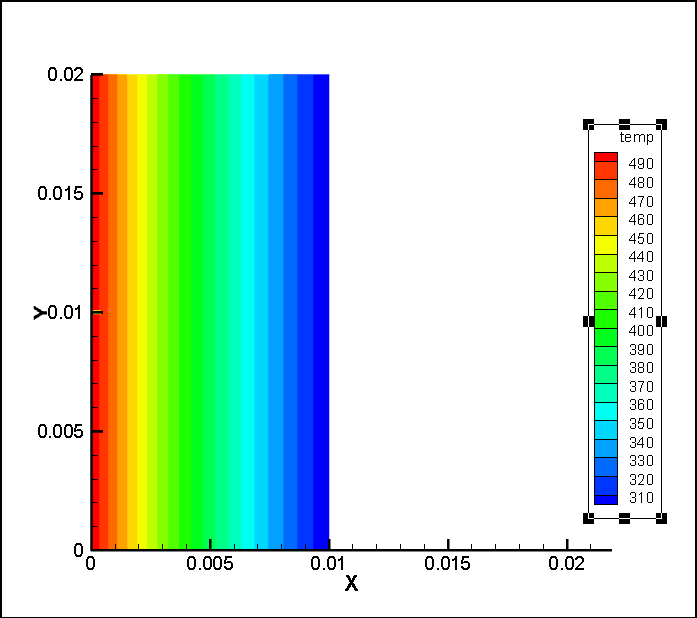
4.1热传导结果 19
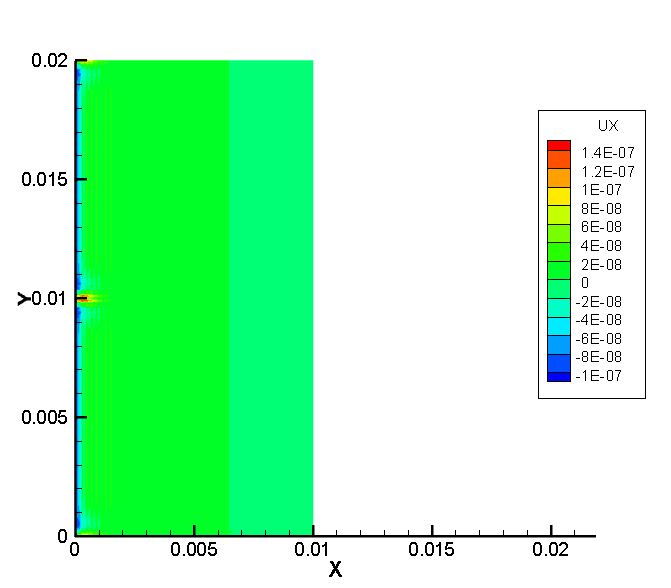
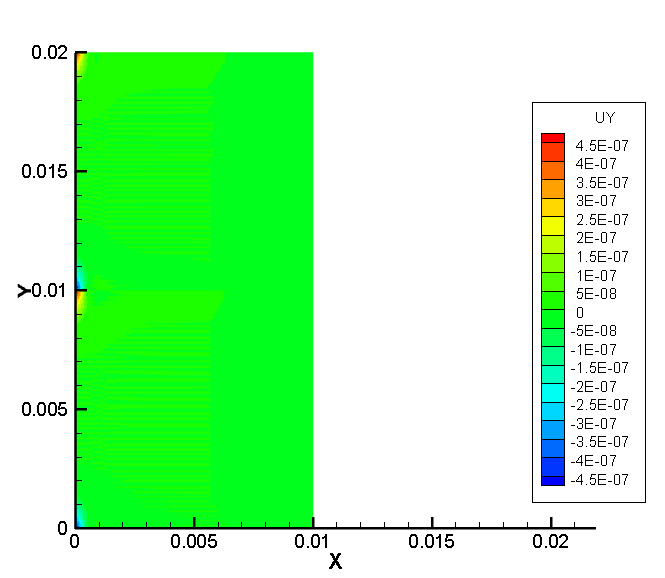
4.2 位移场的求解及结果分析 20
第5章 结论与展望 24
5.1 结论 24
5.2 展望 24
参考文献 25
致谢 26
第1章 绪论
1.1 研究背景
随着科技的发展,以及各个国家在高端科技的快速发展,让上天入地成为可能,也让一些以前不可能的发明成为现实。比如航空航天、潜水艇等高科技项目,还有渗入到我们生活中的海底隧道、大跨度桥梁等。这些项目给我们的生活带来了很多的便利,也让我们探索和认识到了很多新的东西。但是这些项目的发展也并不是一帆风顺的。因为这些项目很多情况下要处于非常极度危险的情况下,所以对其制造所需的材料就有很高的要求。所以这些项目的发展也是伴随着新的材料的发展而发展的。尤其是在从世纪四十年代开始,各种的复合材料的研究和应用都得到了极大的发展。复合材料的分类复杂多样,根据组分的不同,可以分为金属和金属的复合材料、非金属和金属的复合材料还有非金属和非金属的复合材料。复合材料不仅可以保持各组分材料性能的优点,而且因为各个组分之间的关联,它的一些材料属性也会较单一的材料而言有明显的提高。所以说复合材料可以满足人们在极端环境下的材料需求。
超高温陶瓷复合材料主要包括一些过渡族金属的难熔硼化物、碳化物和氮化物,它们的熔点都在3000℃以上。同时也具有较高的热导率、适中的热膨胀系数以及良好的抗氧化烧蚀性能,可以在2000℃以上的氧化环境中实现长时间非烧蚀,是一种非常有前途的超高温防热材料[1]。所以可以应用在一些极端(超高温)的情况下,有着非常广泛的用途。有望应用于航天飞机的发动机,太空往返飞行器和大气层内高超音速飞行器的鼻锥、前缘以及发动机燃烧室的关键部位,以及金属高温熔炼和连铸用的电极、坩埚等。因此国内外非常重视对超高温陶瓷复合材料的的研究。
但是超高温陶瓷复合材料是一种典型的脆性材料,在热冲击载荷或者极端加热的条件下很容易发生热冲击失效,产生难以想象的后果[2]。因此研究其热冲击性能,并对其进行改善是非常重要的。
同时阅读文献发现前人的研究大多不考虑变形对温度的影响,或者是弱热力耦合的形式进行研究,本文采用的是完全热力耦合的形式进行研究。[3]
1.2 超高温陶瓷复合材料的抗热冲击研究现状
目前来说,测试超高温陶瓷复合材料的抗热冲击性能的实验方法主要分为升温热冲击和降温热冲击。其中升温热冲击主要包括等离子火炬,电弧加热等方法。而降温热冲击则是利用冷却介质使材料快速降温,所以根据所使用的介质不同可以分为油淬、水淬、气淬等[4]。而在以上的方法中,水淬是最常用的实验方法。因为水淬法操作简单,比较容易控制,测量结果较准确。除了实验的研究方法以外,还可以通过软件模拟的方法求解材料在热冲击载荷作用下的分析。
1.3 近场动力学的研究现状
对于经典的连续介质力学理论,我们首先假定了介质的连续性,然后在此基础上建立了有限元法(FEM)等方法,从而用这些方法来求解连续介质力学方面的问题[5]。但是当介质存在裂纹或者不连续的情况下,因为违背了介质的连续性这一前提假设,导致有限元法(FEM)等方法不再适用了。近场动力学(peridynamics)是为了解决不连续的问题而被提出来的。Silling(美国桑迪亚国家实验室,Sandia National Laboratories)在2000年首先提出了基于键的近场动力学(peridynamics)。近场动力学(PD)是一种基于非局部理论的一种新型的数值计算方法[6]。它通过积分代替微分的方法,有效的避免了在裂纹附近求偏导的问题。从而PD理论可以直接用来描述质点域内存在的裂纹萌生及扩展等存在不连续的问题,并且不需要借助其他的理论方法。因此,近场动力学(PD)得到了非常多学者的关注,从而有了更多的研究和发展。
在Silling提出了基于键的近场动力学理论后,因为该理论在求解模型发生裂纹的萌生或者扩展等问题方面有着极大的实用性,所以很多学者利用该理论方法进行了大量的研究分析。在国外的研究方面,Agwai等人应用基于键的进场动力学理论模拟了电子集成电路中裂纹的萌生与扩展现象[7]。同时Kilic2009年在近场动力学理论中引入了材料损伤系数的定义[8]。而在国内沈峰、章青等人利用近场动力学理论模拟了冲击载荷作用下的混凝土结构的破坏过程[9]。王富伟、黄再兴等人利用近场动力学理论模拟了复合材料层合板的冲击损伤问题[10]。刘硕、方国东等人将近场动力学理论和有限元方法耦合,然后用此耦合方法对热传导问题进行了分析和求解。程占起、刘健对基于近场动力学的功能梯度材料(FGM)进行了动态断裂分析[11]。
可以了解到基于键的近场动力学不仅可以用于位移场的求解,而且在温度场的求解方面有着很广泛的应用。还有Oterkus等人在基于键的进场动力学的基础上提出了近场动力学的瞬态传热函数以及完全热力耦合下的模型函数,并给出了它们的无量纲形式。同时分别的对一维、二维、三维的模型进行分析,提出了相对于不同维度的响应函数。
但是由于基于键的近场动力学理论只考虑两个粒子延其连线方向上的相互作用,不能考虑其它方向的作用力,所以该方法所描述的受力和变形情况是不准确的。尤其是在研究三维问题时,由于上式的不准确性导致不管是什么材料,实际应用的泊松比都是0.25。这个问题严重的影响了基于键的近场动力学的应用范围。因此为了解决这个问题,Silling在2007年在近场动力学中引入了变形态和力态两个概念,并提出了在基于键的近场动力学基础上的基于态的近场动力学理论。力态代表的是某个粒子与其邻域内的所有粒子的相互作用的总和。也因此解决了基于键的近场动力学存在的问题。
综上所述,近场动力学理论作为一种非局域的无网格方法因为其在求解不连续问题(裂纹的萌生及扩展)以及多尺度模拟问题时的优越性和广泛适用性[12],所以得到了广大学者的关注,也因此促进了近场动力学理论的发展。尤其是态理论的提出解决了键理论存在的问题,增加了进场动力学的适用性。
1.4 本文主要研究内容
本文研究的是热冲击载荷作用下超高温陶瓷复合材料的热力耦合分析。虽然已经有很多人通多有限元法对相关的内容作了研究,但是由于有限元法的局限性并不能完整的描述这个分析。而且很多研究不考虑热力耦合的问题,或者是弱热力耦合的分析,这种分析的结果虽然与实际情况的差距并不大,但是也存在一定的误差。
- 分析并总结了基于态下的陶瓷本构方程以及基于态的近场动力学的热力耦合方程。
- 设计并编写了程序,用于求解热冲击载荷作用下超高温陶瓷复合材料的热力耦合分析。
- 使用编写的程序,求解出在各个时间点下模型的各个部位的位移、以及应力的分布图。并对得到的结果进行分析。
第3章 近场动力学理论
2.1 近场动力学
近场动力学的提出是为了更好的求解存在裂纹或者一些不连续问题而在2000年由Silling提出来的。近场动力学是一类基于非局部理论的无网格粒子类方法。它是把每个质点域按照一定的体积离散成大量的分布规则的物质点。并且假定质点与其邻域内的每个每个质点都有相互作用。而根据其作用方式的不同,近场动力学被分为基于键的PD理论和基于态的PD理论两类。
2.1.1 基于键的近场动力学
根据基于键的理论,运动方程用来描述粒子和粒子之间的相互作用。假定粒子对粒子的作用力矢量为,粒子对粒子的作用力矢量为。根据牛顿第三定律有与大小相等,方向相反,即
参考构型下将两粒子之间的相对位置(坐标矢量差)记为,即
同时被称为粒子和粒子间相互作用的键(bond-based)。
两粒子之间的相对位移(位移矢量差)记为,即
而力的大小也与粒子与粒子之间的键的伸长率有关,可以通过下式得到
其中力与伸长率之间的关系为
其中是与材料的弹性模量相关的弹性常数,一般与粒子间的距离有关。
从上面的公式中可以得出力不仅和粒子与粒子之间的位置有关,而且与粒子间的位移有关系,因此力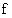 可以用以下形式表示
可以用以下形式表示
然后再根据运动学的平衡方程,质点的惯性力矢量等于其所受的所有内力与外力之和,从而有
其中和分别代表粒子和粒子在时刻的位移,代表作用在粒子上的所有外力。
同时粒子与粒子之间伸长率是有一定的限制的,即当时,粒子间的键就会发生破坏,从而导致粒子间的相互作用力失效。
基于键的PD理论在泊松比0.25时,能够适用于微弹塑性材料存在断裂失效时的研究。但是基于键的理论也存在一定的局限性,例如它的力矢量函数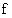 不能表示经典的连续介质力学中材料的本构问题;还有基于键的近场动力学也不能描述材料在受到剪切力作用而产生的塑性变形。
不能表示经典的连续介质力学中材料的本构问题;还有基于键的近场动力学也不能描述材料在受到剪切力作用而产生的塑性变形。
2.1.2 基于键的近场动力学的瞬态热传导方程
基于键的近场动力学不仅可以解决存在断裂失效或者存在不连续的微弹脆性材料的问题,而且还可以解决存在不连续情形的瞬态热传导问题,并且都有其独特的优点。对基于键的近场动力学的瞬态热传导理论,以二维模型为例,在粒子处的热流密度公式为
其中是引入的微导热系数,和分别代表时刻时粒子和粒子的温度,是沿着热键方向的单位矢量,而代表的是粒子的面积。同时为了确保PD热流密度和经典热流密度的一致性,引入了材料的热传导系数和微热导率之间的关系,即
其中表示的是粒子的邻域半径。
基于键的近场动力学的瞬态热传导的平衡方程为
其中代表的是粒子单位体积内的热生成量。
同样的当超过某一极限值热键断裂时,在热键方向的位移就会消失,因此引入“历史相关”函数来表示键是否失效
当粒子间不存在任何裂纹(键没有失效)时,可以通过热键进行热传导;但是当粒子间的键断裂以后,就不能够进行热传导,即通过该热键的热量为零。
通过上述可以了解到基于键的近场动力学的瞬态传热算法在解决存在裂纹(不连续问题)的传热模型时也是可以计算的,但是因为热导率是通过粒子邻域内的等效热流计算得到的,所当模型的材料不均匀或者材料是复合材料等不均匀材料的,就不是那么容易计算出微热导率。
2.1.3基于键的近场动力学的热力耦合方程
Oterkus提出了基于键的近场动力学热力耦合理论的无量纲形式[13],公式如下
式中代表的是粒子的初始温度;代表的是基于键的PD热模量;代表的是单位体积的热生成量。
2.2 基于态的近场动力学热力耦合理论
因为基于键的近场动力学理论存在的各种缺陷,所以在2007年Siliing提出了基于态的近场动力学理论[14]。它引入了变形态和力态的概念,也是通过这个概念使得传统的连续介质力学和近场动力学的理论之间建立了一定的联系,也因此扩充的近场动力学理论的适用范围。态理论和键理论既有相同点又有不同点,相同的方面是它们都采用一样的方式将质点离散化。不同的是态理论中,不再只是考虑两个粒子间的相互作用,而是一个粒子同时与其邻域内的多个粒子都产生相互作用。然后由于粒子和粒子的变形态的不同,它们之间就会产生相互作用的力态,分别为和。
2.2.1 基于态的近场动力学的运动平衡方程
非常规态的基于态的近场动力学的运动方程如下:
其中表示的是以粒子为中心半径为邻域,被称为粒子作用在粒子上的力态,同样的表示粒子作用在粒子上的力态。
根据文献,可以得到力态与第一类皮奥拉-基尔霍夫应力张量之间的关系[15],如下所示:
其中表示的是定义在材料键键长的影响函数;表示的是粒子在参考构型中的对称形变张量,它的计算公式如下所示:
同时在经典连续力学的基础上,可以得到第一类皮奥拉-基尔霍夫应力张量和柯西应力张量之间的关系,即
式中是粒子的变形梯度矩阵,表示变形梯度矩阵的转置矩阵的逆矩阵,表示的是的行列式。
粒子的变形梯度矩阵的定义如下:
其中表示的是粒子和粒子之间的相对位移矢量。
粒子的变形梯度率可以表示为
式中代表的是粒子的速度矢量状态。
粒子的速度梯度张量可以表示为
同时粒子的形变率张量和旋转张量可以由速度梯度张量表示为
对于J-C模型来说形变率由弹性形变率、粘塑性形变率、和热形变率三部分组成。
应变率,代表的是弹性矩阵,公式计算时进行一定的变形,表达式如下
柯西应力的更新公式为
2.2.2 基于态的近场动力学的热力耦合方程
从文献中可以得到完全热力耦合下的的基于态的近场动力学的导热方程[16]如下所示
式中表示的是模型材料的比热容;和分别表示粒子和粒子在时刻下的温度;表示参考温度;表示单位体积的产热速率。
2.3 本构方程的更新
材料的本构方程一般是指利用数学表达式来表示出某种材料的应力-应变关系。因此在选用不同的材料时都需要更新其本构方程。
2.3.1 陶瓷材料的本构方程
针对陶瓷材料而言,很多学者在大量的实验的基础上推导出了能够适用于陶瓷材料的本构模型。其中包括修改的Wilkins模型、Rajendran-Grove模型、Plastic-Kinematic模型、JH模型以及在其基础上改进得到的JH2模型[17]。虽然这些不同的陶瓷材料模型都能进行陶瓷材料相关的模拟分析,但是JH2模型也因为其简明扼要的表达形式还有其计算得到的预测结果比较准确成为了目前使用最广的陶瓷材料模型之一。因此本文也主要介绍了JH2陶瓷模型的函数方程。
关于JH2模型的函数方程,主要包括强度方程,状态方程以及该模型对陶瓷材料的损伤的定义。
- 强度方程
JH2模型的无量纲的等效应力是:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
![D:\Documents\Tencent Files\2354595172\Image\C2C\00TYM}JNUI_8R6(`AED@`]W.png](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw7183_202021810530378.png)
![D:\Documents\Tencent Files\2354595172\Image\C2C\S6MNAV]{]1RBA@I[F5}(}C8.png](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw7183_202021810530383.png)