石墨烯形态对其聚合物基纳米复合材料热力学性能的影响毕业论文
2020-04-06 13:08:34
摘 要
石墨烯是一种由sp2杂化碳原子组成的二维结构材料,其独特的纳米结构和优异的热、机械和电性能,使其在传感器、催化、电池和超级电容器等技术领域具有潜在的应用。同时,将石墨烯作为增强填料,在聚合物基体中加入少量的石墨烯即可以有效地改善单一高分子的性能,是制备高性能聚合物基复合材料的有效途径。近年来,石墨烯/聚合物基纳米复合材料优越的热性能、机械性能、电性能和耐磨损性等,使其在电子、宇航、燃料电池等方面具有广阔的应用前景。石墨烯具有超高的导热系数,理论上加入少量的石墨烯可以大幅提高聚合物基体的导热系数。但是石墨烯作为一种纳米填充剂,其与聚合物基体间的弱界面粘附效应导致界面会产生较大的界面热阻,进而影响石墨烯与聚合物基体间的热传导性能。此外,石墨烯的填充浓度、尺寸以及形态等同样是影响其热传导性能的主要因素。
本文考虑石墨烯在聚合物基体中的形状、尺寸、浓度、界面热阻等因素,基于细观力学有效介质理论,获得石墨烯/聚合物基纳米复合材料等效热传导系数的表征形式,并分析了界面热阻效应、石墨烯浓度、尺度、形态等因素对其热传导性能的影响。主要研究工作及结果如下:
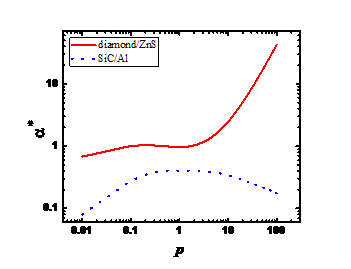
首先,针对复合材料的热力学性能,基于Maxwell有效介质理论理论,利用细观力学方法推导出具有任意形状填充相复合材料导热系数的广义有效性能表征形式。以此理论表征形式为基础,文中预测了颗粒diamond增强ZnS复合材料与SiC颗粒增强铝基复合材料的热导率,并将所得结果与实验结果进行了对比,验证所得热传导广义表征形式的准确性。
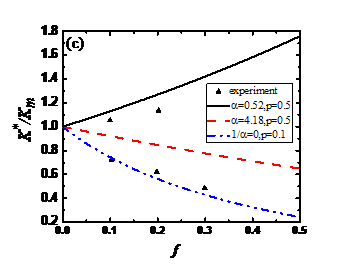
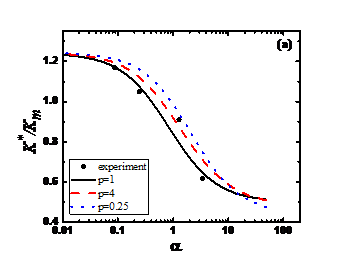
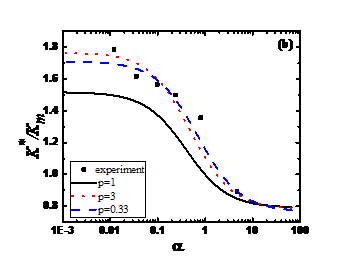
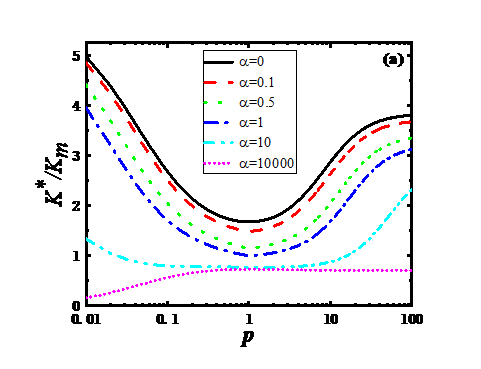
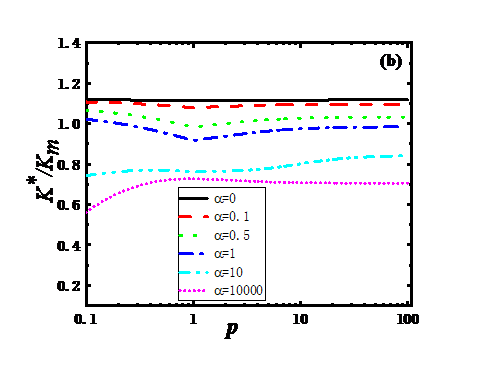
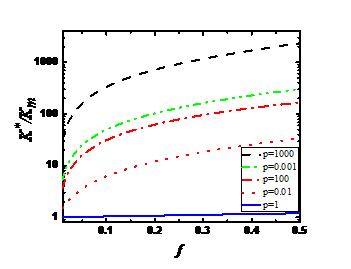
其次,我们基于已建立的复合材料热传导性能的广义表征形式,针对石墨烯/聚合物基纳米复合材料的有效导热系数进行了理论预测,分析了界面热阻、石墨烯浓度、尺度、形态等因素对其聚合物基纳米复合材料热力学性能(热传导系数)的影响规律。
关键词:石墨烯/聚合物基纳米复合材料,有效介质理论,有效导热系数,界面热阻。
Abstract
Graphene is a two-dimensional structure material composed of sp2 hybridized carbon atoms. Its unique nanostructure and excellent thermal, mechanical and electrical properties make it potentially useful in sensors, catalysis, batteries, and supercapacitors. At the same time, using graphene as a reinforcing filler, adding a small amount of graphene to the polymer matrix can effectively improve the performance of a single polymer, which is an effective way to prepare high-performance polymer matrix composites. In recent years, graphene/polymer-based nanocomposites have been widely used in electronics, aerospace, and fuel cells due to their superior thermal properties, mechanical properties, electrical properties, and abrasion resistance. Graphene has a high thermal conductivity, and theoretically adding a small amount of graphene can significantly increase the thermal conductivity of the polymer matrix. However, as a nanofiller, graphene has a weak interfacial adhesion effect with the polymer matrix, which results in a large interfacial thermal resistance at the interface, which in turn affects the thermal conductivity between the graphene and the polymer matrix. In addition, the filling concentration, size, and morphology of graphene are also the main factors affecting its thermal conductivity.
In this paper, the shape, size, concentration, and interface thermal resistance of graphene in the polymer matrix are considered. Based on the meso-mechanical effective medium theory, the characterization of the equivalent thermal conductivity of the graphene/polymer-based nanocomposite is obtained and analyzed. The effect of interface thermal resistance, graphene concentration, scale, morphology, and other factors on its thermal conductivity. The main research work and results are as follows:
First of all, according to Maxwell effective medium theory, based on the thermodynamic properties of composite materials, a generalized effective performance characterization form of the thermal conductivity of the composite material with arbitrary shape filled phase is deduced by meso-mechanics method. Based on this theoretical representation, we predicted the thermal conductivity of granular diamond-enhanced ZnS composites and SiC particle-reinforced aluminum matrix composites, and compared the results with experimental results to verify the accuracy of the resulting generalized representation of thermal conduction.
Secondly, based on the generalized characterization of the thermal conductivity of composites, we have theoretically predicted the effective thermal conductivity of graphene/polymer-based nanocomposites, and analyzed the interfacial thermal resistance, graphene concentration, scale, morphology, and other factors. The effect of thermodynamic properties (thermal conductivity) of polymer-based nanocomposites.
Key Words:Graphene/polymer-based nanocomposites; Effective medium theory; effective thermal conductivity; interface thermal resistance.
目 录
摘 要 I
Abstract II
第1章 绪 论 1
1.1 研究背景 1
1.2 研究现状 1
1.2.1石墨烯的简介 1
1.2.2石墨烯/聚合物基纳米复合材料的导热原理 2
1.2.3石墨烯/聚合物基纳米复合材料导热性能的研究现状 2
1.3本文的研究目的和研究内容 3
第2章 纳米复合材料热导率的有效性能分析 4
2.1纳米复合材料热导率的有效性能表征 4
2.2 不同形态下复合材料的等效热导率 6
2.2.1 均匀分布的长纤维 6
2.2.2 层压平板 6
2.2.3球体 7
2.2.4完全随机分布的椭球状颗粒 8
第3章 数值计算结果及讨论 9
3.1纳米复合材料的数值结果计算与实验比较 9
3.2石墨烯/聚合物基纳米复合材料的数值结果计算与讨论 13
第4章 结论 18
参考文献 19
致 谢 21
第1章 绪 论
1.1 研究背景
随着现代科学技术的发展,过去的传统材料性能单一,而性能单一的材料是无法适应现代工业和科技的需求,因为性能单一在实际应用中具有巨大的局限性。因此人们特别希望可以找到一种具有多种优良的性质的现代材料来代替传统单一局限性的材料来满足生产发展的需求。现如今高度集成化和小型化的电子元件在这个互联网信息化时代具有不可替代的作用,而这种电子元件在高频率的工作下会积聚大量的热,积聚的大量的热会使得元件局部温度过高,而高热环境使得半导体的电子元件工作不稳定,并且还会极大地缩短其工作寿命,增加了工作成本,降低了工作效率[1]。因此国内外对于导热材料的研究和开发,始终充满了极大地兴趣。
科技进步日新月异,电子产品功率密度随之迅猛增加,高效的散热材料成为信息、通讯和储能技术进步的关键问题。只有开发出导热性能优良的材料,现代电子、光电、光子器件和系统的性能才能得到提升,从而促进下一代集成电路(ICs)、三维(3D)集成和超快的大功率密度通信设备的发展。纯的高分子材料质量轻、抗腐蚀,但是导热性能差,填充高导热性能的材料进行复合是开发电子电气领域导热材料的有效途径[2]。
1.2 研究现状
如今有关石墨烯形态尺寸对其聚合物基纳米复合材料热力学性能影响的研究主要是针对复合材料的导热机制展开的[3],明晰形态尺寸,界面热阻,填充物浓度等因素对其热力学性能的影响,可以为改善石墨烯纳米复合材料的导热性能提供一定的理论基础。推导出复合材料的形态尺寸对其有效热导率影响的广义表征形式是研究石墨烯/聚合物纳米复合材料导热机制的重要基础,早期应用比较广泛的有Hasselman和Johnson[4]在Maxwell和Rayleigh的经典理论[5]、MG有效介质理论模型[6]、Bruggeman积分嵌入原理[7],Torquato和Rintoul[8]以及Lipton和Vernescu[9]开发的边界技术等理论基础。
1.2.1石墨烯的简介
石墨烯有具有优良的力学性能,电学特性以及热学性能和光学性能。研究表明,石墨烯强度高,韧性好,它的理论杨氏模量达1.0TPa,固有的拉伸强度为130Gpa[3]。石墨烯电子迁移率受温度因素影响特别小,其载流子迁移率是硅材料的10倍多,大约为15000cm2/(V·s),比载流子迁移率最高的物质锑化铟(InSb)还要高一倍多。而且石墨烯导热性能比碳纳米管还要好,单层石墨烯是导热系数最高的碳元素材料,高达5300W/mK。当它作为载体时,导热系数也可达600W/mK。此外,石墨烯的弹道热导率可以使单位圆周和长度的碳纳米管的弹道热导率的下限下移[10]。石墨烯具有非常良好的光学特性,可当作优良的吸波材料[11]。
1.2.2石墨烯/聚合物基纳米复合材料的导热原理
在室温下,大多数的纯的高分子材料本身导热性能并不理想,如纯的聚乙烯(PE)导热系数为0.33W/mK,聚氯乙烯(PVC)的导热系数为0.13~0.17W/mK,聚苯乙烯(PS)导热系数为0.08W/mK,有机玻璃(PMMA)导热系数为0.17~0.25W/mK,尼龙(Nylon)材料导热系数为0.25W/mK,环氧树脂导热系数约为0.2W/mK等,由此可见这些常用的高分子材料导热性能极差[1]。而在这些高分子材料中加入导热性良好的填充剂是提高其导热性能的重要途径。
石墨烯/聚合物纳米复合材料的导热性能由石墨烯填充物和基体本身的导热性能共同决定。而通过上节1.2.1中的介绍我们了解到而石墨烯填充物的导热性远远优于高分子基体的导热性。当石墨烯填充材料的填充量比较小的时候,基体材料和石墨烯填充物能够在同一个体系中均匀分布,但相互之间几乎没有相互作用[12]。当石墨烯填充材料的量达到某一较大值时,填料与高分子基体之间便会形成相互作用,使体系形成导热网链。导热网链的取向方向对体系的导热性能影响特别显著,当其取向与热流方向平行时,复合材料的导热性能便会极大地提高。填料和基体两者可以看作复合材料体系之中的两个热阻,石墨烯可以看作一个小的热阻,而基体导热性能差,因此可以将其看作一个大的热阻,如果热流没有沿导热网链流动,那么热流在穿过导热性能差的高分子基体时便会受到巨大阻碍,从而导致材料导热性能极差,这便是石墨烯/聚合物纳米复合材料的导热原理[13]。
1.2.3石墨烯/聚合物基纳米复合材料导热性能的研究现状
复合材料不同成分相之间的界面热阻可能是界面处机械或化学粘附性差和热膨胀不匹配形成的。Kapitza发现金属-液体界面温度的不连续性后,这种界面抗性被称为Kapitza热阻,用RBd符号来表示。很多复合材料导热系数的研究表明:界面热阻对复合材料的有效导热系数K*影响显著。虽然大家已经知道复合材料的界面效应,但是关于这种效应的理论研究最近才开始。这个问题的前两个理论分析分别是由Hasselman和Johnson[4]以及Benvensite[14]进行的。Hasselman和Johnson在Maxwell和Rayleigh[5]的经典理论上考虑界面效应和粒径因素对球形颗粒和圆柱形纤维增强基体复合材料的影响,推导出用于计算等效热传导系数的Maxwell-Garnett有效介质近似方法[6]。Benvensite[14]基于微观力学模型也得到了同样的结果。Every[15]等人在Maxwell-Garnett有效介质近似理论[6]的基础上,基于Bruggeman积分嵌入原理[7]给出了非对称形式的有效介质理论方法此外,Davis和Artz[16]基于有限元数值分析方法,针对球形颗粒增强纳米复合材料的热传导系数与MG-EMA的分析结果进行了对比,证实了细观力学有效介质理论的有效性。对于非球形颗粒增强纳米复合材料,Hatta和Taya[17]以及Benveniste和Miloh[18]分别建立了理论分析模型,考虑了短纤维在基体中的排布方式(定向排列或随机取向)对复合材料等效热传导系数的影响。在此基础上,Dunn和Taya[19]修正了MT均匀化方法[20],分析了具有包覆层短纤维的形状以及界面热阻效应对复合材料等效热导率的影响,预测了K*对颗粒形状的非常强的依赖性。这种现象将在本文中被重点关注。
其他不同的理论研究路线是最近由Torquato和Rintoul[8]以及Lipton和Vernescu开发的边界技术[9]。Torquato和Rintoul通过使用最小能量原理提出了球形颗粒复合材料K*更严格的界限。其界限包含有较高阶相关函数的未知参数。Lipton和Vernescu也衍生出了不同的界限,其下界包含了一个所谓的形成因子m0(即:该复合材料的归一化有效导电性,将粒子以相同形状的空洞取代,并且对这个因子m0的确定很敏感。然而,这一形成因素在理论上可以用多种方法来确定。
1.3本文的研究目的和研究内容
通过对相关文献的综述和分析我们可以将对于石墨烯形态对其聚合物基纳米复合材料热力学性能的影响划分为以下几个层次。首先基于细观力学基础应用Maxwell有效介质理论推导出具有界面热阻的任意颗粒复合材料有效热导率的广义表征形式,然后推导出复合材料在四种简单极限情况下的表达式,得出复合材料的MG-EMA结果。
本文在前人研究的基础上,基于Maxwell有效介质理论和细观力学方法得到考虑界面热阻、石墨烯浓度、形态和尺寸等因素的复合材料等效热传导系数表征形式,并且应用Matlab编程软件,完成程序编写工作,并且开展数值分析工作,利用Origin软件绘制图形,最后将数值分析结果与实验结果进行对比,修正理论模型,分析了界面热阻效应、石墨烯浓度、尺度、形态等因素对聚合物基纳米复合材料的热力学性能(热传导系数)的影响规律。
第2章 纳米复合材料热导率的有效性能分析
本章将有效介质理论方法与Kapitza接触热阻[21]的基本概念相结合,得到了预测任意颗粒状复合材料有效热导率有效性能的广义表征形式,并将理论分析结果和实验结果进行了对比,推导了几种简单极限情形下的理论分析结果。此外,本章所提出的分析方法不仅能够描述填充颗粒的尺寸和形状对其热传导率的影响,而且考虑了界面热阻的影响。
2.1纳米复合材料热导率的有效性能表征
根据Nan的多重散射理论[22],我们可以将复合介质中的热传导率从点到点的变化的变量表示为K(r)=K0 K’(r),其中K0表示均匀介质的常数部分,K’(r)是一个任意的波动部分。对于由K0定义的均匀介质和整个复合介质通过使用格林函数G[23]和转移矩阵T,可以得到温度梯度分布的精确解[24]。所得的复合材料的有效导热系数K*表示为
(2.1)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: