摘 要

作业车间调度问题研究是在时间上对系统有限的资源进行合理有效的配置，以达到满足特定调度目标的要求。作为一种需满足设备和工艺复杂约束条件的组合优化问题，作业车间调度问题具有求解复杂性和约束复杂性的特点。随着问题规模和约束条件的增大，工序间的相互制约关系更加复杂，可能出现的解的数量会呈指数级增长，这些特点给作业车间调度问题的求解增加了难度。由于可行域性状十分复杂，难以用传统优化方式求解，求解包含复杂关联约束的作业车间调度问题(JSSP: Job Shop Scheduling Problem)依然是难点问题。本研究将该问题分解为“设备分配”和“工序排序”两个相互耦合的问题，分别发挥遗传算法求解“设备分配”和蚁群算法求解“工序排序”的优势，一级优化采用遗传算法求解工序的设备分配方案，二级优化采用蚁群算法求解与设备分配方案对应的工序最优排序，将一级优化结果作为蚂蚁的约束条件输入到二级迭代过程，将二级优化结果作为适应度信息反馈给一级迭代过程，从而形成完整的二级嵌套循环迭代过程。通过一系列改进策略，如：基于工序的整数编码策略、基于设备类型的多节点交叉策略、基于逆向遍历的可行路径形成策略、基于最短加工时间的信息素播洒与更新策略等等，构造了集成遗传算法与蚁群算法于同一循环体的二级嵌套混合算法。并以一个具体的作业车间调度问题为例，将典型的仿生算法、一般优化算法，手工调度的方法和二级嵌套混合仿生算法的求解过程和结果进行对比，并通过比对试验验证了所提算法的可靠性和优越性，为求解包含复杂关联约束的JSSP提供了新思路和新方法。

关键词：作业车间调度问题；复杂关联约束；遗传算法；蚁群算法；二级嵌套混合仿生算法

Abstract

Job shop scheduling problem is to allocate the limited resources of the system to meet the requirements of specific scheduling objectives reasonably and effectively. As a combinatorial optimization problem with the complex constraints of equipment and process, job shop scheduling problem has the characteristics of solving complexity and constraints complexity. With the increase of problem scale and constraints, the mutual constraints between processes become more complex, and the number of possible solutions will increase exponentially. These characteristics make it more difficult to solve job shop scheduling problems. Due to the complexity of the feasible region, it is still a difficult problem to solve job shop scheduling problems with complex associated constraints. Through decomposing the problem into two mutual coupling problems of "equipment allocation" and "process sequencing", a two level nested hybrid algorithm integrating genetic algorithm and ant colony optimization algorithm in the same loop body is constructed, giving full play to the advantages of genetic algorithm in solving "equipment assignment" and "ant colony optimization algorithm" in solving "process sequencing" respectively. The first-level optimization uses genetic algorithm to solve the equipment allocation scheme and the second-level optimization uses ant colony algorithm to solve the optimal sequencing corresponding to the equipment allocation scheme. The results of first-level optimization are input into the second-level iteration process as constraints of ants. As fitness information, the result of second-level optimization is fed back to the first-level iteration, thus a complete second-order nested loop iteration process is formed. A series of improved strategies, such as the integer encoding strategy based on process, multi node cross strategy based on machine type, feasible path forming strategy based on reverse ergodic, pheromone broadcasting and updating strategy based on the shortest processing time, and so on, are detailed. Taking a specific job shop scheduling problem as an example, this paper compares the solving process and results of typical bionic algorithm, general optimization algorithm, manual scheduling method and two-level nested hybrid bionic algorithm. The reliability and superiority of the proposed algorithm, which provides new ideas and new methods for solving JSSP with complex associated constraints, are verified by comparison tests.

Key words: job shop scheduling problem；complex associated constraints； genetic algorithm；ant colony optimization.

目录

第1章 绪论--------------------------------------------------------------------------------------------------1

第2章 二级嵌套模型及基本思路-----------------------------------------------------------------------3

第3章 面向设备分配的遗传算法-----------------------------------------------------------------------7

3.1 改进的编码策略：基于工序的整数编码策略-------------------------------------------------7

3.2 改进的交叉策略：基于设备类型的多节点交叉策略----------------------------------------8

3.3 改进的变异策略：设备类别区间内基因互换-------------------------------------------------9

第4章 面向工序排序的基于逆向遍历的蚁群算法-------------------------------------------------10

4.1 逆向遍历形成可行路径的方法------------------------------------------------------------------10

4.2 路径确定的前提下单个蚂蚁最优解的求解方法---------------------------------------------10

4.3 信息素播洒与更新策略---------------------------------------------------------------------------11

第5章 比较试验研究-------------------------------------------------------------------------------------12

5.1 研究背景---------------------------------------------------------------------------------------------12

5.2 遗传算法---------------------------------------------------------------------------------------------12

5.3 蚁群算法---------------------------------------------------------------------------------------------12

5.4 一般优化算法---------------------------------------------------------------------------------------13

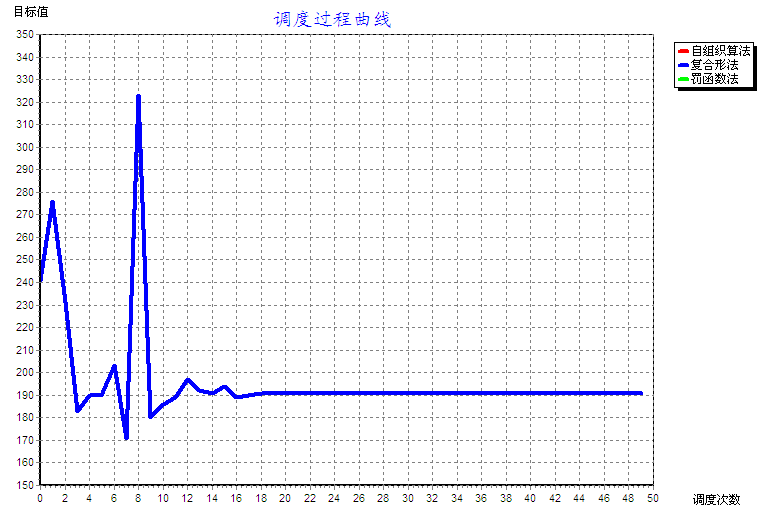
5.4.1 复合形法----------------------------------------------------------------------------------------13

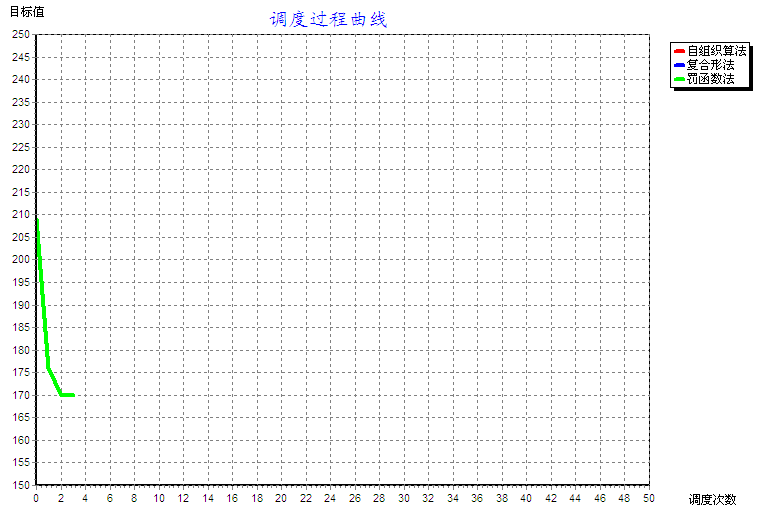
5.4.2 罚函数法----------------------------------------------------------------------------------------15

5.4.3 基于拓扑排序的算法-------------------------------------------------------------------------17

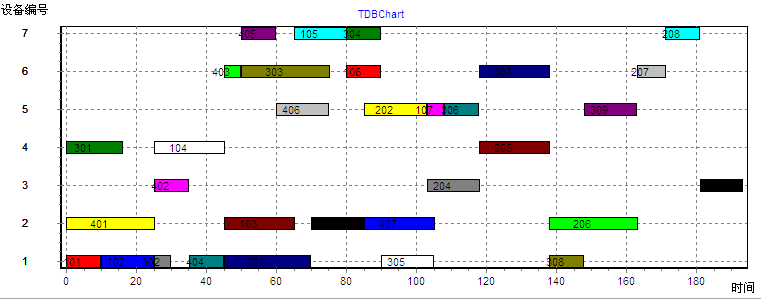
5.5 手工调度的方法------------------------------------------------------------------------------------20

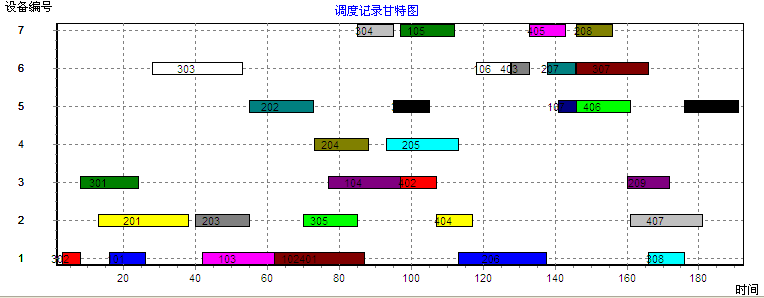
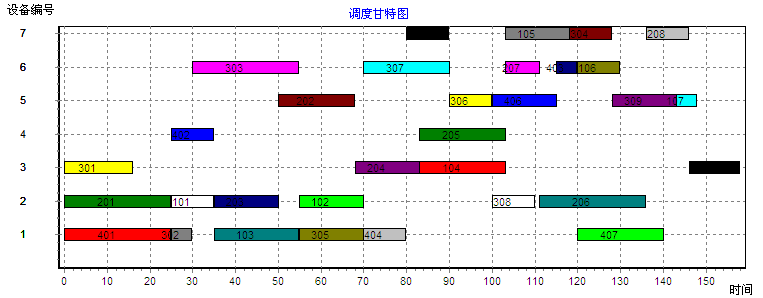
5.6 二级嵌套混合仿生算法---------------------------------------------------------------------------21

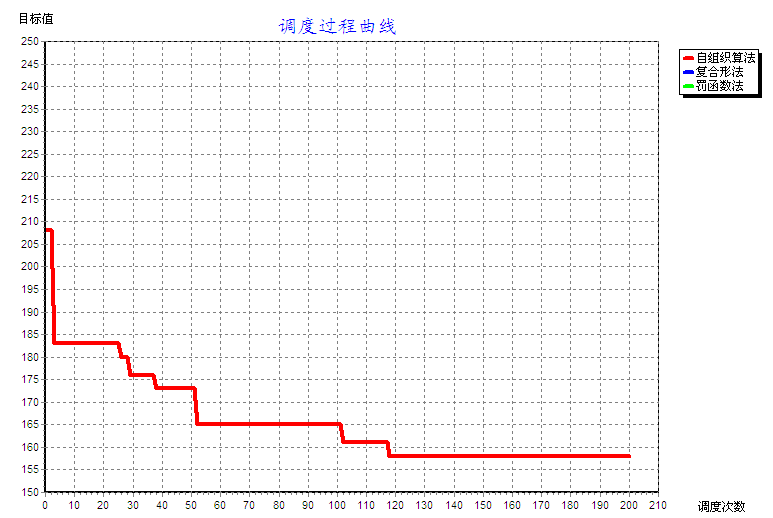
5.7 求解结果分析---------------------------------------------------------------------------------------22

第6章 结论-------------------------------------------------------------------------------------------------24

参考文献------------------------------------------------------------------------------------------------------24

致谢------------------------------------------------------------------------------------------------------------26

第1章 绪论

作业车间调度问题是一种需要满足加工工艺和加工设备之间复杂约束条件的组合优化问题，属于NP-hard问题，若用传统优化方式求解不仅优化程度较低，并且效率不高。作业车间调度问题可描述为：生产加工任务中共包含n个工件，其中每个工件包括至少一道的并联或串联的工序，每个工件的加工时间均不相同，要求在m台设备上依次进行相应的加工。每个工件的各道工序都必须在与之相对应的加工类型的设备上进行。以使得总加工时间最短，总拖期时间最短或提前/拖期惩罚代价最小为优化目标对问题进行调度，求出一个最优解，并确定最终的调度优化方案。

JSSP的求解过程有如下的一些假设：工件与工件之间的加工顺序没有前后次序的要求，均保持独立。生产过程所涉及到的加工设备有k类共m台。工序与工序之间具有串联或并联的优先次序关系，即只有完成某工序的前序工序，才可启动该工序。一道工序一旦启动，不可中断加工。同一台设备上不能同时加工两道工序。同一工件不能同时有两道工序在进行加工。一个工件可在不同设备上加工，而一道工序不可在不同加工类型的设备上加工。

作为一种需满足设备和工艺复杂约束条件的组合优化问题，作业车间调度问题具有求解复杂性和约束复杂性的特点。随着问题规模和约束条件的增大，工序间的相互制约关系更加复杂，可能出现的解的数量会呈指数级增长，这些特点给作业车间调度问题的求解增加了难度。作业车间调度问题是NP-hard问题，用传统优化方式求解不仅优化程度低，并且效率低下。如何有效可靠的求解JSSP已成为了组合优化领域的一个研究重点和热点[1-3]，并已取得较多成果[4-7]。

目前作业车间调度较常用的方法有：基于规则的启发式算法[5]、遗传算法、蚁群算法、粒子群算法、蜂群算法、以及将各种算法机制相结合形成的混合算法等等。在大部分研究中，运用最广泛的算法包括遗传算法与蚁群算法。遗传算法主要通过改进编码方式或改进适应度设置方法来进行优化[6-8]，如Kurdi等以最大限度地缩短制造周期为目标，提出了一种有效的新的孤岛模型遗传算法，并提出了一种新的自然激励进化模型和一种新的自然激励迁移选择机制，提高搜索的多样性，延缓早熟收敛，提高经典孤岛模型遗传算法的有效性[8]。又如Driss等提出了一种新的遗传算法，该算法采用了一种新的染色体表示方法，不同的交叉和变异策略，并在一系列基准数据集上进行了验证[9]。蚁群算法作为一种新方法，在解决作业车间调度问题时有较优的表现。但是，其可行域的复杂性决定了现有的蚁群算法在求解作业车间调度问题时收敛可靠性较低、优化能力不强。针对上述两个难点，蚁群算法主要有一阶变量和二阶变量两类或衍生改进的算法[10-11]。如Zhao等针对多目标作业车间调度问题，建立了多目标作业车间调度问题的数学模型，将问题分解为两个子问题，即工艺路线决策和任务排序，并提出了一种两代（父子）帕累托蚁群算法，用于解决作业车间调度问题，并制定一个可行的调度方案。其中，父代蚁群系统解决了灵活的处理路径决策问题，从替代的处理节点集中选择最合适的处理节点集，子代蚁群系统解决了父蚁群系统生成的进程任务集的排序问题[10]。混合算法通常是将另一个算法的机制融合到主算法中，如Zhang等提出了一种动态环境下作业车间调度/再调度问题的混合方法，构建了一个完全分布式的MAS结构，通过代理之间的协商进行搜索解决方案[12]。或对主算法进行改进，如Kulkarni等提出了一种基于仿真优化的混合建模方法和公式，并介绍了两个新的决策变量：控制器延迟和队列优先级[13]。或混合遗传算法，如Chang等提出了一种新的编码机制来解决无效的作业分配，采用田口法对遗传算法的参数进行优化以增加找到染色体最优解和多样性的概率[14]，又如Kudakci等提出了一种考虑随机作业，机器故障和加工时间变化等生产环境中不可避免的动态事件的混合遗传算法[15]。虽然这些算法在求解JSSP方面有较多成果，但也存在一定的局限，如调度规模较小，如Huang等提出了几种基于蚁群优化的混合算法来解决多目标车间调度问题，提出一种新的信息素和贪婪启发式函数，三种新的状态转移规则函数，一种改进解质的灵活的局部搜索算法和一种基于粒子群优化的参数自适应调整算法[16]。另外，现有研究中工序关系主要以串行为主等，对存在串行、并行、甚至嵌套关系的复杂关联约束调度问题，研究还比较少。

综上可知，JSSP求解时搜索范围之所以庞大和复杂，是因为其设备分配和工序排序之间有复杂且紧密的相互干涉，导致较低的搜索效率和收敛可靠性。尤其当问题规模较大、并且存在复杂关联约束时，解空间的复杂度呈几何级数上升，这种情况下，即使寻找可行解也有较大的困难。针对上述问题及难点，本研究以包含复杂关联关系并具有一定规模的JSSP为研究对象，将问题分解为“设备分配”和“工序排序”两个相互耦合的问题，分别发挥遗传算法在求解配置问题方面的优势和蚁群算法在求解排序方面的优势，构造将两种方法集成到一个完整循环体的二级嵌套混合仿生算法，以在可接受的迭代次数内求得比较满意的设备分配和工序排序方案。

第2章 二级嵌套模型及基本思路

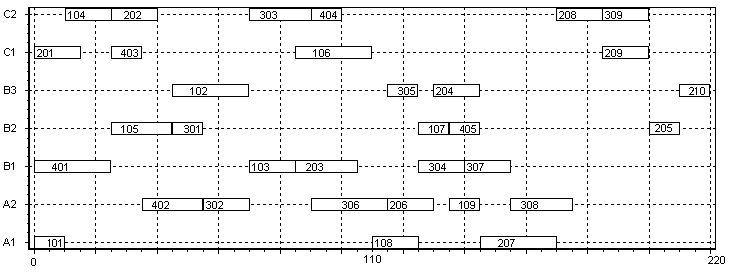
为了能采用混合仿生算法求解复杂关联约束问题，首先，从二级嵌套的角度构造复杂关联调度的数学模型。以一个生产汽车发动机零部件的作业车间为例，该作业车间共生产四类零件：节油器、连杆总成、油箱和增压器。生产加工过程所涉及到的工件工序与加工设备的关联关系如图1所示，每个工件的加工顺序和加工时间不同。由图2.1可知，每项独立的任务均由串联或并联进行的工序组成，共有33道工序。调度的目标是：将这些工序合理的分配到A(A1，A2)、B(B1，B2，B3)、C(C1，C2)三类共7台设备上，使得总加工时间最短。需要满足的约束包括：

(1)前序工序约束：某工序必须在完工时间先于它的其它工序之后才能启动，则这些必须预先完成的工序就称之为某工序的前序工序。如工序404，其前序工序为402，则402完成了，就(才)可以启动404，工序309，其前序工序为工序307和工序308，则307，308都完成了，就(才)可以启动工序309。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：