基于LSH的轨迹相似度搜索毕业论文
2020-02-18 11:54:10
摘 要
轨迹数据是对一个或多个移动对象的运动过程进行采样所获得的数据信息,常见的有车辆轨迹数据和行人轨迹数据。通过对轨迹数据进行分析,可以实现许多方便人们生活的功能。例如在道路拥挤区域进行交通信号的优化,从而减少车辆与行人的等待时间,或者通过合理的规划路径来缓解交通拥挤的状况等等。但这些功能都离不开一些基础的操作,例如轨迹的相似性查询,即给定一条查询轨迹,在轨迹数据库中找到和查询轨迹最相似的一条或多条轨迹数据。
然而,随着GPS设备的普及,轨迹数据规模呈爆发式增长,如何快速地在海量的轨迹数据中找到相似的轨迹(最近邻搜索问题)成为了一个难题。受限于当前计算机的计算与存储能力,线性扫描算法进行一次相似性查询可能需要几秒甚至十几秒。这一时间花费是难以接受的。因此人们需要一个能够在海量轨迹数据中快速搜索相似轨迹的方法。
局部敏感哈希(LSH)算法在近似最近邻搜索问题的求解上,有着十分优秀的效果,它通过合理的筛选机制,选取出可能的候选最近邻数据,减少了需要计算真实距离的轨迹数量,这大大加快了最近邻搜索的求解速度。
本文主要研究使用局部敏感哈希对轨迹数据进行近似最近邻搜索的方法,通过减少需要比较的候选轨迹数量,加快了最近邻搜索速度。并且该方法能够适用于目前流行的Hausdoff,Frechet轨迹相似性度量标准。
实验在真实数据集上进行,结果显示,使用局部敏感哈希算法进行近似轨迹最近邻搜索能够有效的减少计算量,在削减了80%的计算量的情况下,能够保证搜索结果的召回率在80%以上。
关键词:局部敏感哈希;近似最近邻搜索;轨迹数据
ABSTRACT
The trajectory data is data information obtained by sampling the motion process of one or more moving objects, such as vehicle trajectory data and pedestrian trajectory data. By analyzing the trajectory data, many functions that are more convenient for people to live can be realized. For example, traffic signals are optimized in road crowded areas to reduce waiting time for vehicles and pedestrians, or to ease traffic congestion through reasonable planning paths. However, these functions are inseparable from some basic operations, such as the similarity query of the trajectory, that is, given a query trajectory, one or more trajectory data that are most similar to the trajectory are found in the trajectory database.
However, with the popularity of GPS devices, the scale of trajectory data has exploded. How to quickly find similar trajectories in the massive trajectory data (nearest neighbor search problem) has become a problem. Limited by the computing and storage capabilities of current computers, a linear scan algorithm may require a few seconds or even a dozen seconds to perform a similarity query. This time is unacceptable. So people need a way to quickly search for similar trajectories in massive trajectory data.
The locality sensitive hash (LSH) algorithm has a very good effect on solving the nearest neighbor search problem. It selects the possible candidate nearest neighbor data through a reasonable filtering mechanism, which reduces the number of tracks that need to calculate the real distance. This greatly speeds up the solution of nearest neighbor searches.
This paper mainly studies the method of approximate nearest neighbor search for trajectory data by using locality sensitive hashes. By reducing the number of candidate trajectories that need to be compared, the nearest neighbor search speed is accelerated. And the method can be applied to the currently popular Hausdoff, Frechet trajectory similarity metric
The experiment is carried out on the real data set. The results show that using the locality sensitive hash algorithm for the trajectory approximate nearest neighbor search can effectively reduce the amount of calculation,and the recall rate of search results can be guaranteed to be higher than 80% when the computation amount is reduced by 80%.
Key Words:Locality-Sensitive Hashing;approximate nearest neighbor search;trajectory data
目录
第一章 绪论 1
1.1研究背景与意义 1
1.2国内外研究现状 2
1.3本文主要工作及组织结构 4
第二章 局部敏感哈希和轨迹相似性相关知识 5
2.1预备知识:轨迹相似性度量标准 5
2.2预备知识:局部敏感哈希 6
第三章 局部敏感哈希实现近似轨迹最近邻搜索 9
3.1 Hausdoff距离下的近似最近邻搜索 10
3.1.1算法设计与伪代码描述 10
3.1.2 Hausdoff距离下的局部敏感哈希函数 11
3.2 Frechet距离下的近似最近邻搜索 12
3.2.1算法设计与伪代码描述 12
3.2.2 Frechet距离下的局部敏感哈希函数 14
3.3算法总结 14
第四章 实验设计与算法性能分析 15
4.1评价指标 15
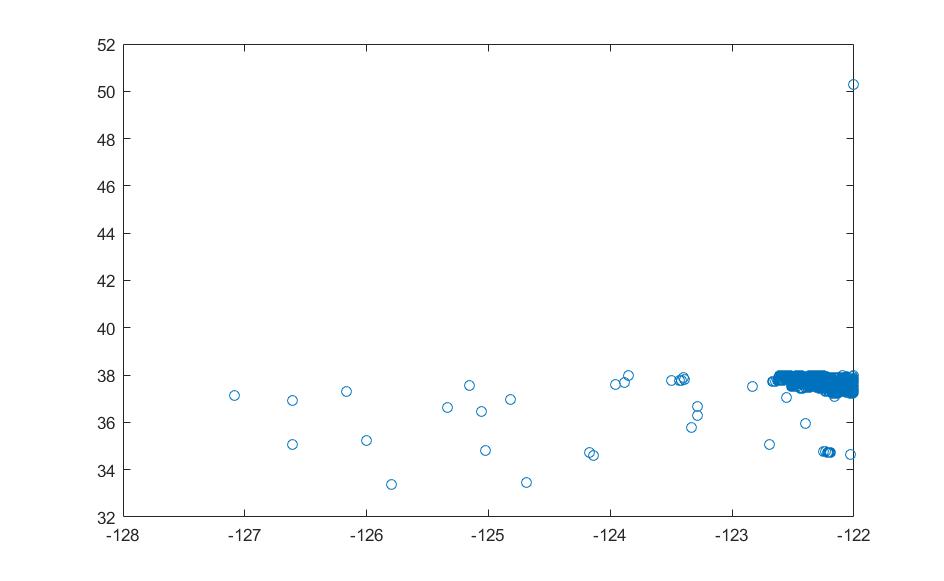
4.2数据集选择与数据处理 15
4.3轨迹数据中噪声对算法的影响 16
4.4参数选取 17
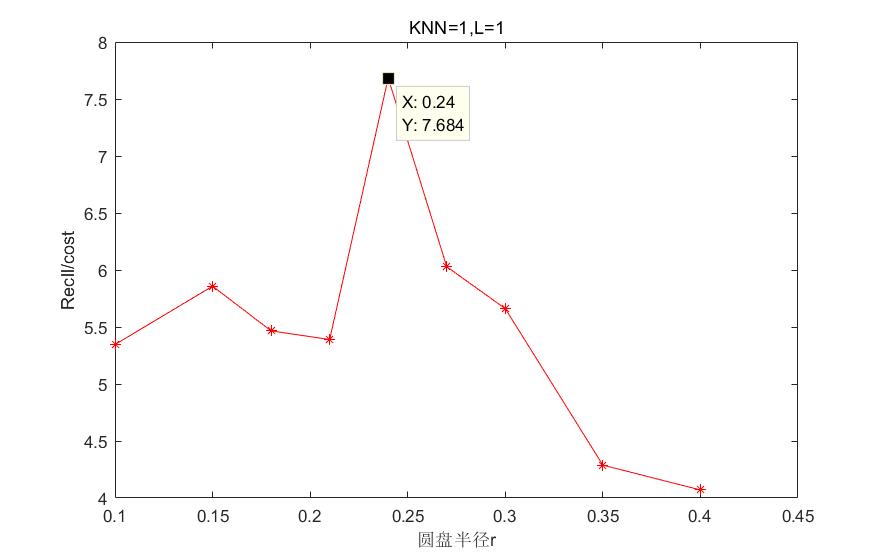
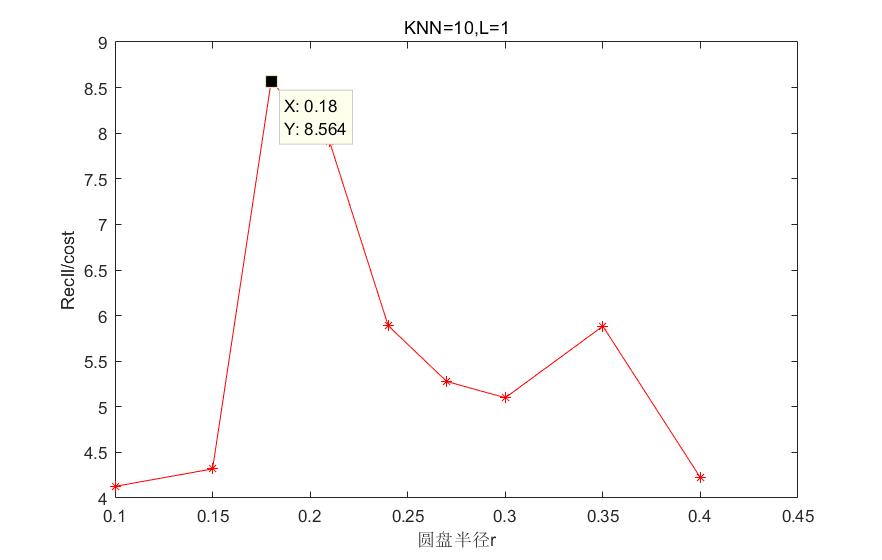
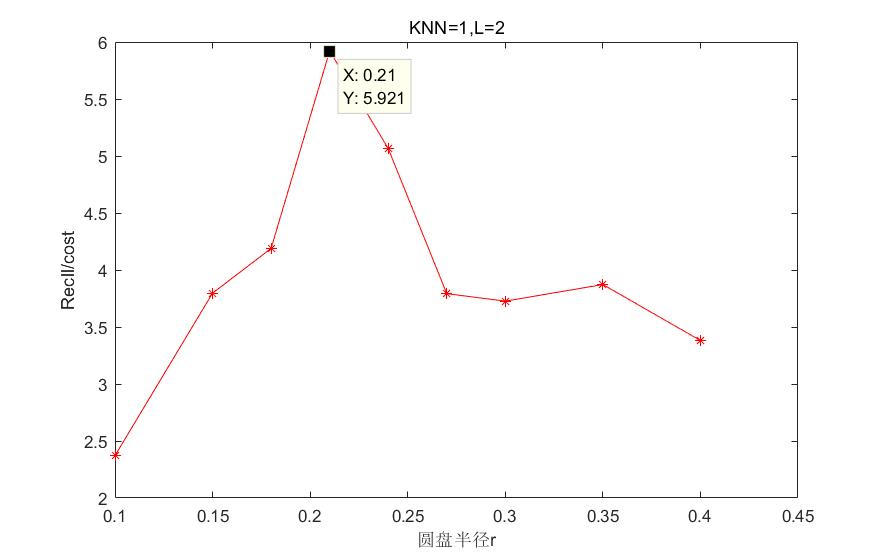
4.4.1 Hausdoff距离下算法参数的选取 17
4.4.2 Hausdoff距离下算法性能分析 20
4.4.3 Frechet距离下算法参数的选取 21
4.4.4 Frechet距离下算法性能分析 22
4.4.5实验总结 23
第五章 总结与展望 24
5.1工作总结 24
5.2工作展望 24
致谢 25
参考文献 26
第一章 绪论
本章详细阐述了研究领域的背景与意义,国内外的研究技术体系以及存在的问题,并明确了研究的目的与内容。
1.1研究背景与意义
轨迹数据在当前的大数据时代中有着越来越重要的作用。通常来说,轨迹数据是对一个或多个移动对象的运动过程进行采样所获得的数据信息,例如通过车载GPS设备或者行人随身携带的GPS设备,按固定时间间隔采样位置信息,并将这些位置信息进行组合,便能够得到车辆轨迹数据和行人轨迹数据。通过对轨迹数据进行分析,可以实现许多方便人们生活的功能。例如在道路拥挤区域进行交通信号的优化,从而减少车辆与行人的等待时间,或者通过合理的规划路径来缓解交通拥挤的状况等等。但这些功能都离不开一些基础的操作,例如轨迹的相似性查询,即给定一条查询轨迹,在轨迹数据库中找到和查询轨迹最相似的一条或多条轨迹数据。
然而,随着GPS设备的普及,轨迹数据规模呈爆发式增长,这造成轨迹数据库中包含的数据量可能高达几百万,几千万,甚至上亿条。并且,轨迹相似性的度量不是简单的计算两点之间的欧式距离,通常人们会使用Hausdoff距离,当需要考虑轨迹自身的顺序特点时则会使用Frechet距离,以及DTW距离。然而这些距离度量方法的计算是十分复杂的,如果使用动态规划计算两条长度为m的轨迹的Hausdoff距离,Frechet距离或者DTW距离,其时间复杂度为,这一时间开销是难以接受的。
由于轨迹数据规模庞大和计算两条轨迹之间的相似性需要很大的时间开销,这导致快速地在海量的轨迹数据中找到相似的轨迹(最近邻搜索问题)成为了一个难题。受限于当前计算机的计算与存储能力,线性扫描算法进行一次相似性查询可能需要几秒,十几秒甚至更高(这取决于数据规模),显然,这一时间花费是难以接受的。因此人们需要一个能够在海量轨迹数据中快速搜索相似轨迹的方法。
研究发现,精确的最近邻搜索需要关于d的线性的查询时间或指数的空间,这也被称为“维数灾难”。这表示,随着数据维数的增加,所需要的查询时间或者空间都会快速增加,给最近邻求解带来困难。尽管经过了几十年的努力,目前仍然没有十分优秀的算法去解决精确最近邻问题。事实上,对于足够大的维度d,无论是从理论还是实践,目前存在的算法仅仅比线性搜索(和数据集中的每一个数据进行比较)的方法好一点。在[[1]]中展示了,对于足够大的d,全部基于索引技术的方法都要比暴力搜索慢。基于上述原因,研究人员提出通过近似搜索来突破运行时间的瓶颈,即允许查询结果存在一定误差,这被称作c-ANN查询。它具体指的是,给定查询数据q,在数据集中找到数据p,数据p和q之间的距离要小于等于c倍的查询数据q和其真实最近邻数据p*的距离。也就是说,其中是数据之间的距离度量。
在许多需要进行轨迹的相似性查询的场合,近似轨迹搜索的结果和精确轨迹搜索的结果几乎一样好,足以满足人们的使用要求,同时又能大量的减少查询时间,因此本文的重点在于快速地在海量的轨迹数据中找到近似的相似轨迹。
1.2国内外研究现状
最近邻(NN)搜索问题在低维空间中能够被很好的解决, 然而,随着数据维度增多达到几百或更高时,搜索时间和空间占用都可能以指数式上升,这一现象被称作“维数灾难”。不幸的是,在模式识别、信息检索等领域,高维数据经常被使用,因此研究如何解决高维空间中的最近邻搜索问题是十分重要的。但事实上,对于足够大的维度m,无论从理论分析,或是实际研究中,人们都不能提出一个比线性扫描算法有效的多的算法,最多只能产生些许作用。在[1]表明,对于足够大的维度m,基于空间划分的索引算法要慢于线性扫描算法。因此,为了突破时间的瓶颈,研究人员将注意力转移到近似最近邻(ANN)搜索问题上。在许多情况下,近似最近邻搜索完全能够满足人们的使用需求。
局部敏感哈希(LSH)是解决近似最近邻搜索问题的最著名的索引方法之一,它最初是作为一个理论方法被Indyk和Motwani提出[[2]],局部敏感哈希的基本思想是,哈希函数通过将数据点投影到随机超平面上,生成数据点的哈希位。统计概率保证在原空间中相邻的点在超平面中很可能彼此相邻。Gionis和Indyk等学者在[[3]]中提出了一种适用于汉明空间的局部敏感哈希方案,但它仅当数据点位于汉明空间时,该算法才能够比较快的进行查询。虽然作者提出了将空间的数据转换成汉明空间数据的方法,但它会以一个较大的常数因子来增加查询时间和错误率,同时增加了算法的复杂度。 Datar和Immorlica等学者在[[4]]中提出了一种适用于空间的局部敏感哈希(E2LSH)方案,E2LSH是欧氏空间中第一个支持近似最近邻查询的局部敏感哈希方法。在查询目标和最近邻结果之间的距离为一个确定的半径r时,该算法表现性良好。
Qin Lv和Josephson等学者在[[5]]中提出了多探针LSH。它不仅检查与查询点位于同一桶中的数据点,而且探测可能在哈希表中包含结果的多个桶,这导致使用更少的哈希表。但是,它仍然需要在不同半径处构建散列表。LSB-tree[[6]]的方案,是第一个不需要在不同半径构建哈希表的方案。它将哈希值分组为一维z阶值,并使用b树进行索引。不同半径的索引项可以在b树的相应范围内检索。Junhao Gan 和 Jianlin Feng等学者在[[7]]中改进了LSB-tree的方法,并提出了C2LSH的方案。他们引入了碰撞计数和虚拟哈希的方法,它为每个哈希表使用一个哈希函数,这样当查询半径增加时,要读取的哈希桶的数量不会成倍增加。Qiang Huang 和 Jianlin Feng等学者在CL2SH的基础上进行了改进,并在[[8]]中提出了一种被称作QALSH的方案。它在获得查询目标后,根据查询目标划定哈希桶边界。同样引入了碰撞计数和虚拟哈希的方法,但QALSH改进了C2LSH仅支持近似比c gt; 4且c必须是整数的平方这一缺点。QALSH支持比c gt; 1,这增加了算法的可用性。
Yifang Sun 和Wei Wang在[[9]]中提出了SRS方案。该方案通过2-stable分布将数据点从高维空间投影到低维空间中,其主要的发现是低维空间中的距离比上高维空间中的距离服从卡方分布,这提供了一个很好的上下界。因此SRS能够首先在低维空间中查找距离查询目标最近的多个数据点,然后在原高维空间中计算这些数据点和查询目标的距离,并返回距离最小的数据点。SRS方案实现简单,其大幅度减少了空间开销。Yuxin Zheng等学者在[[10]]中提出了LazyLSH的方案,它仅需要一次索引实现了计算多个空间结果的目标。 由于哈希桶中存在大量的假正数据点会大量的增加查询时间。为了解决这个问题,Satuluri和Parthasarathy在[[11]]中提出了BayesLSH。它结合了贝叶斯统计理论,并使用局部敏感哈希方法进行临近点筛选和相似性估计。它可以快速的清除假正数据点,这显著的减少了查询时间。 基本的局部敏感哈希方法遇到的另一主要困难是需要访问许多和查询点位于同一个桶中的数据候选点,这会导致大量的I/O开销。为了处理这个问题,Yingfan Liu 和 Jiangtao Cui等学者在[[12]]中提出了SortingKeys-LSH的方法,它通过对复合散列键进行排序,以便在索引中对数据点进行相应的排序,以降低I/O成本。
为了将局部敏感哈希应用于轨迹数据,Indyk[[13]]提出了一种适用于Frechet距离的局部敏感哈希形式,然而,这个方法对空间的需求十分巨大,将该方法应用在GPS数据集上是不实际的。Driemel和Silvestri[15]提出了一个更简单的适用于轨迹的局部敏感哈希机制,这个方法将轨迹的顶点放到网格当中,以顶点在网格中的顺序作为哈希函数。
计算两条轨迹之间的距离是十分具有挑战性的,对于长度为m的两条轨迹,Frechet距离和DTW距离都需要的开销[[14]]。研究结果表明,使用亚二次方的时间计算Frechet距离是不可能的。因此,对于含有n条轨迹的数据集,简单的邻近搜索算法需要花费的时间。Indyk的局部敏感哈希方法花费了的时间和找到一个近似解。然而,当轨迹数据的m较大时,这个方法则面临着很大的挑战。
Driemel和Silvestri[[15]]使用更直观的方法提出适用于Frechet和DTW距离的局部敏感哈希方法。他们第一个策略是将轨迹放置到随机的网格当中,轨迹的哈希值是顶点在网格遍历的顺序。对于两条轨迹P和Q,它们哈希值相同的概率和网格尺寸,轨迹长度m,以及Frechet距离函数有关。
其它的处理大型轨迹数据集的方式是构造一个和初始轨迹相似的轨迹。The Douglas-Peucker 算法[[16]]在这种类型的算法中较为流行,它在许多情况下表现都比较好。
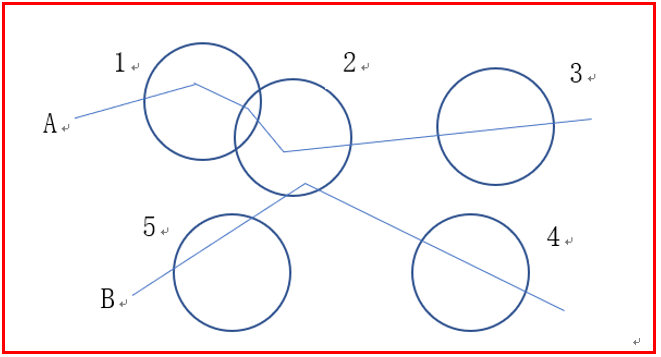
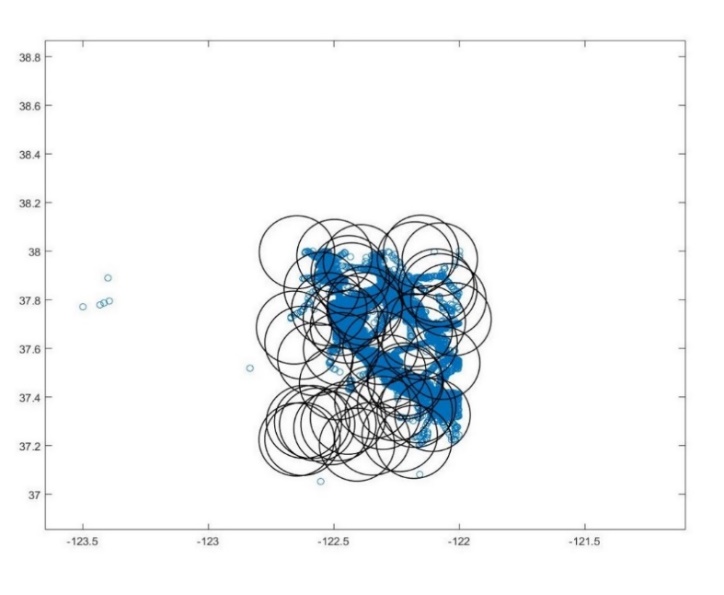
Maria Astefanaei[17]将轨迹数据放置到随机生成的圆盘,根据轨迹和圆盘相交的方式,形成两种方案。第一种方案判断轨迹是否在圆盘当中,若轨迹在圆盘当中,则置1,反之则置0,形成了类似于0101011的序列,以此作为哈希函数的哈希值,该方案可用来处理Hausdoff的情况,在仅计算轨迹总数目的20%的条件下,可以达到80%以上的准确度。第二种方案判断轨迹进出圆盘的顺序,形成类似于2,3,1,4,1的序列,该方案可用来处理Frechet的情况,其效果表现同样良好。
1.3本文主要工作及组织结构
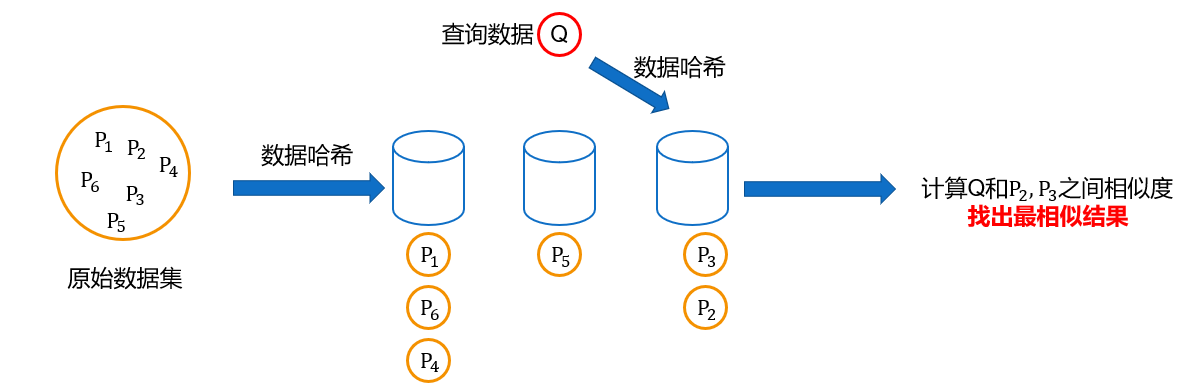
本文将Maria Astefanaei[[17]]提出的轨迹数据转换的方法和局部敏感哈希进行结合并以此进行近似最近邻轨迹数据搜索,且独特地的引入multiply-shift hashing 方案[18]来缩短[17]中轨迹数据转换结果,从而改善查询时间增加,空间开销增大的缺点。同时分析了[17]中方法在存在噪声时算法表现性差的原因,并给出了解决方案,实现对原有算法的优化。算法主要思路如下:首先构建哈希表,然后将原始轨迹数据集进行转换,将转换后的轨迹数据使用multiply-shift hashing 方案进行压缩得到新的哈希结果,并将结果存入不同的桶中。对于查询轨迹,同样进行数据转换,压缩得到哈希结果,然后找到哈希结果对应的桶。对于桶中已存在的轨迹数据认为是候选轨迹,计算候选轨迹和查询轨迹之间的真实距离,并进行排序,最后返回距离查询轨迹最近的轨迹数据。
整个实验在真实数据集下测试,对Hausdoff距离和Frechet距离进行了性能分析。实验结果显示,对于Hausdoff距离,在仅计算轨迹总数目的20%的条件下,可以达到80%以上的准确度,对于Frechet距离,在仅计算轨迹总数目的20%的条件下,可以达到85%以上的准确度。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: