含非线性介质光腔耦合光力系统中的可控光学双稳态研究毕业论文
2020-02-18 10:32:00
摘 要
近年来,人们对腔光力系统的研究取得了很大的进展,非线性光学和光学双稳态也有了重要的理论成果和实际应用。随着可控光学双稳态在混沌效应和量子信息中的应用,腔光力系统在未来必然会继续熠熠生辉。
本文以最简单的光腔为基础,介绍了光腔力学的基本知识和光与物质作用的基本规律,对基本参量进行了定义,通过光腔的输入-输出规律引出了光机耦合原理。再介绍了光学谐振器的非线性效应和光学双稳态,并分析了光学双稳态在实际中的作用效果。最后引出了我们的工作,完成对含非线性介质光腔耦合光力系统的双稳态的控制,通过系统总哈密顿量,在平均场近似的条件下推导出了输入-输出曲线的表达式,并以此为基础,进行数值仿真,得出了腔内光子数的多种曲线,并总结了控制光学双稳态的理论方式。
在文末我们对光机系统近年来的重要应用进行了总结,并对应用前景做出了展望,在未来腔光力系统依然有很多值得我们去探寻的内容。
关键词:光学谐振器,光腔力学,非线性光学,光学双稳态
Abstract
In recent years, great progress has been made in the research of cavity photodynamic system. Nonlinear optics and optical bistability also have important theoretical results and practical applications. With the application of controllable optical bistability in chaotic effect and quantum information, the cavity photodynamic system will continue to shine in the future.
Based on the simplest optical cavity, this paper introduces the basic knowledge of optical cavity mechanics and the basic law of the interaction between light and matter, defines the basic parameters, and derives the principle of optical-mechanical coupling through the input-output law of the optical cavity. Then the non-linear effect and optical bistability of optical resonator are introduced, and the effect of optical bistability in practice is analyzed. Finally, our work is introduced to complete the bistability control of optical cavity coupled optical force system with non-linear medium. Through the total Hamiltonian of the system, the expression of the input-output curve is deduced under the condition of the average field approximation. On this basis, numerical simulation is carried out, and various curves of photon number in the cavity are obtained, and the theoretical ways of controlling optical bistability are summarized.
At the end of this paper, we summarize the important applications of optical system in recent years, and make a prospect of its application prospects. There are still many things worth exploring in the future.
Key words: optical resonator, optical cavity mechanics, nonlinear optics, optical bistability
目录
摘要 I
Abstract II
第1章 绪论 1
1.1 光腔 1
1.2 光学双稳态 1
1.3 本论文的主要内容和安排 2
第2章 光腔力学 4
2.1 光腔力学的发展背景 4
2.2 光学谐振器 5
2.3 光腔的输入输出形式 5
2.4 光机耦合原理 6
2.4.1 辐射压力与光机耦合 6
2.4.2 哈密顿量 7
第3章 光腔中的非线性效应 9
3.1 非线性效应的研究背景 9
3.2 克尔效应 9
第4章 光学双稳态 11
4.1 光学双稳态理论与研究背景 11
4.2 光学双稳态的基本特性 12
第5章 理论模型 13
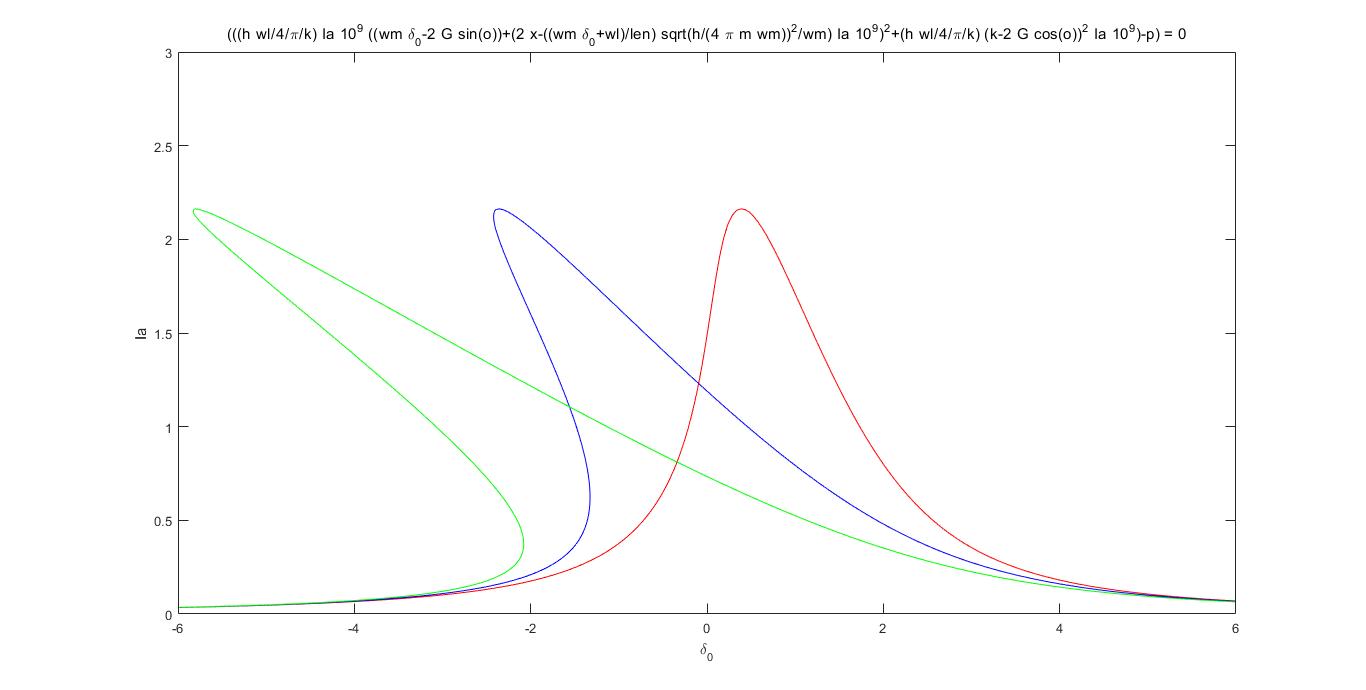
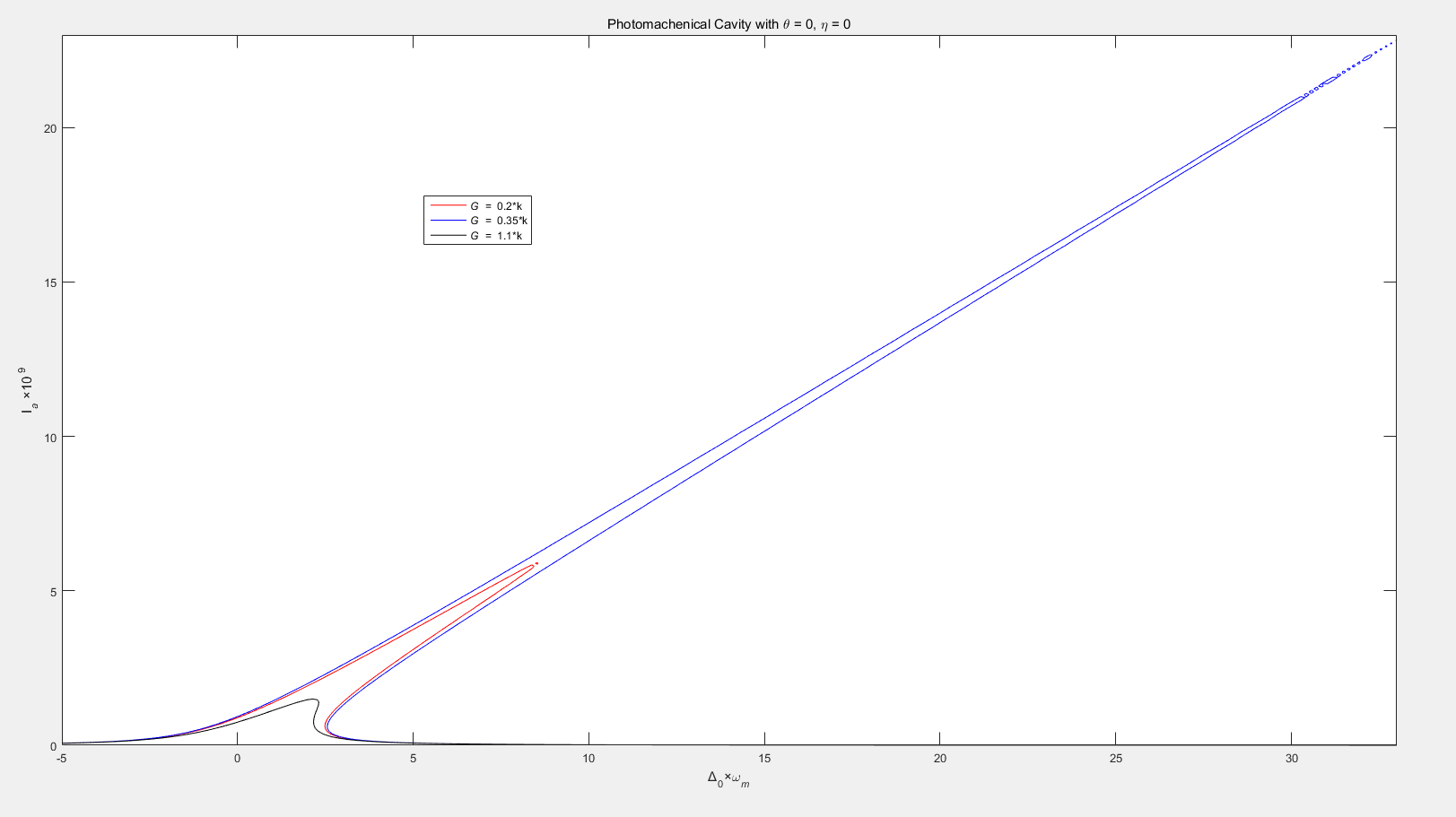
5.1 模型与公式 13
5.2 双稳性讨论 15
5.3 图像分析 15
5.4 结论 18
第6章 总结与展望 19
致谢 20
参考文献 21
第1章 绪论
1.1 光腔
光腔又称为光学谐振器,在激活的光学物质两端恰当的间隔放两个反射镜,就组成了最简单的开放式光学谐振腔。光腔的发展史上,最早出现的是平行平面腔,它的组成仅仅依靠两块平行的平面反射镜,在光学上我们称之为法布里-珀罗谐振器,简称F-P腔。随着激光技术的发展,用两块具有公共轴线的球面镜组成的谐振腔得到了普遍的采用,这类腔被称之为共轴球面腔,平行平面腔是共轴球面腔的特例。在理论分析中,往往认为这种腔的侧面没有光学边界,所以这类腔被人们称为开放式光学谐振腔,简称为开腔。根据损耗的高低,开腔一般可以分为三种:稳定腔、非稳定腔以及临界腔[1]。
由两个以上的反射镜构成的光腔被称为环形腔或折叠腔,在其中插入透镜等光学器件便可组成复合腔。在折叠腔中,往返运动的两束光有固定的相位,会因为干涉而产生驻波,所以折叠腔通常被称为驻波腔;而在环形腔中,顺、逆时针传播的两道光束,由于互相独立,不能形成驻波,所以环形腔又被称为行波腔。
另一类光学谐振器是波导谐振器,半导体激光器用的就是典型的介质波导腔,它的光传输区的尺寸与光的波长是一个数量级的,介质区的折射率高于包围区,所以近轴光线会在侧壁面发生全反射,并由于波导端面的解理区而产生端面反馈,在波导谐振器中,不能忽略侧面边界的效应。
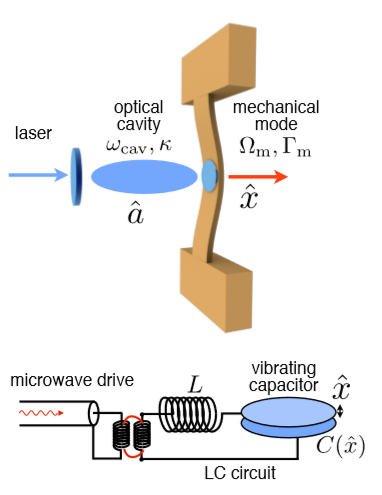
在图1.1中列出了各种光学机械装置的模样,按照质量,从上到下、从左到右它们分别是:悬挂式宏观镜、悬挂式微观镜、悬浮微柱、蹦床谐振器、悬浮膜、混合光机系统、微环面、半导体微盘谐振器、双盘微谐振器、近场耦合纳米机械振子、独立的波导、光学微球谐振器、超导微波电路中的微机械薄膜、光子晶体缺陷腔(2D)、光子晶体纳米波束(1D)、双弦“拉链”腔、腔中的纳米棒、冷原子与一个光学腔耦合。
1.2 光学双稳态
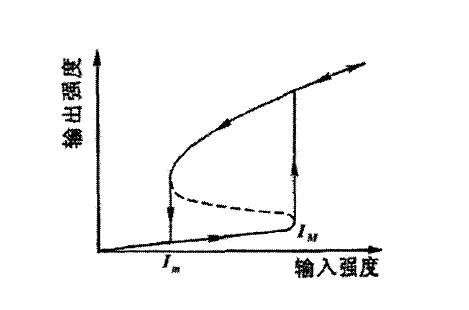
由于激光理论和计算的发展,光学双稳态在1969年被理论预言,1975年首次在实验中被观察到。目前在理论方面,光学双稳态已经比较完善,为了将其应用于光通信迅、 光信息处理和光计算机之中,正在研究它的开关、 记忆、限幅、 放大、振荡和各种光逻辑功能,。并努力探求高速度、低功耗、小尺寸和室温运转的器件[2]。
若是一个光机系统在给定某一个输出光强的条件下,存在两种输出光强状态的可能性,并且通过一些手段可以实现两种状态之间的转换,那么我们就可以称这个光机系统具有光学双稳性。
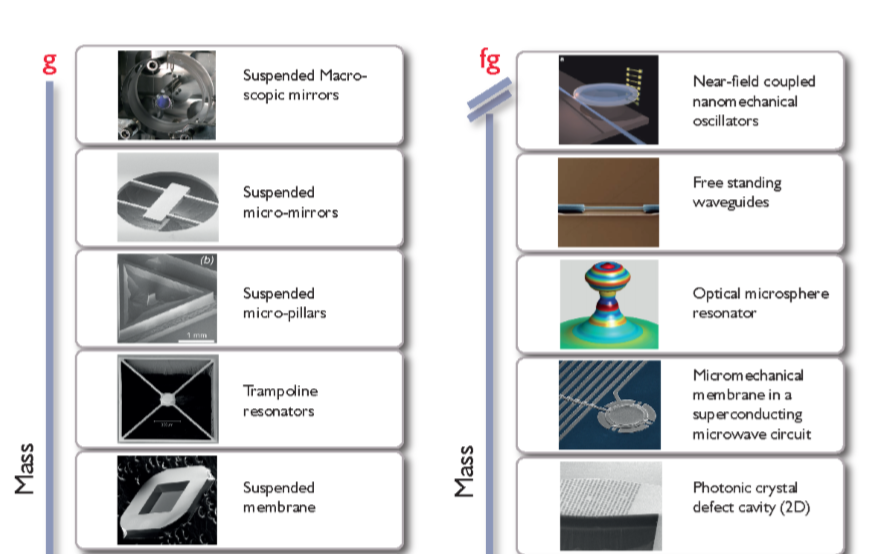
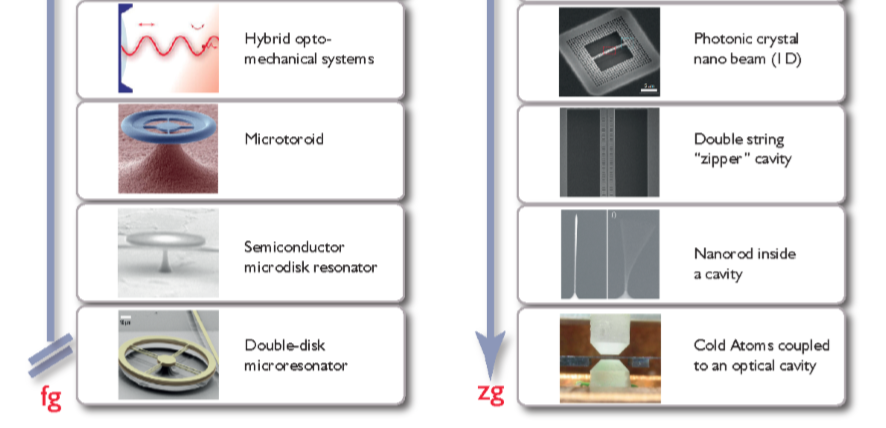
图1.1 上图[3],根据质量的排序展示了一系列光学机械设备
1.3 本论文的主要内容和安排
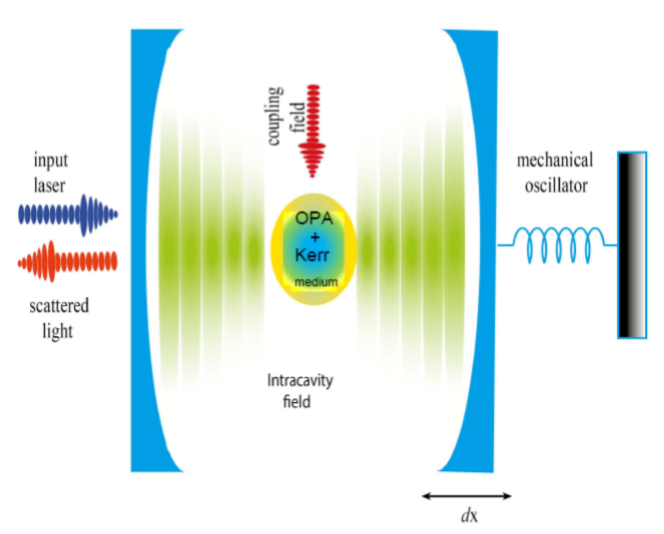
本文主要分析和研究了非线性介质光腔耦合光力系统中的可控光学双稳态,从光机系统出发,到非线性介质,再到光学双稳态,最后通过公式与图像结合的形式,对双稳态的控制条件进行了分析。
第一章是引言,介绍了本文研究的基本内容。
第二章介绍了光腔力学,从光腔力学的背景出发,然后介绍了光腔力学的发展过程以及常见的光机系统,从最简单的法布里-珀罗腔出发,介绍了光腔力学的基本概念,还介绍了光机耦合原理,说明了光子与机械谐振器的耦合形式。
第三章介绍了非线性介质和非线性效应,并简略描述了非线性光学系统、克尔介质和克尔效应。
第四章介绍了光学双稳态,从光学双稳态的研究背景与成果介绍到它的光学特性和现象,并简要分析了光学双稳态的图像。
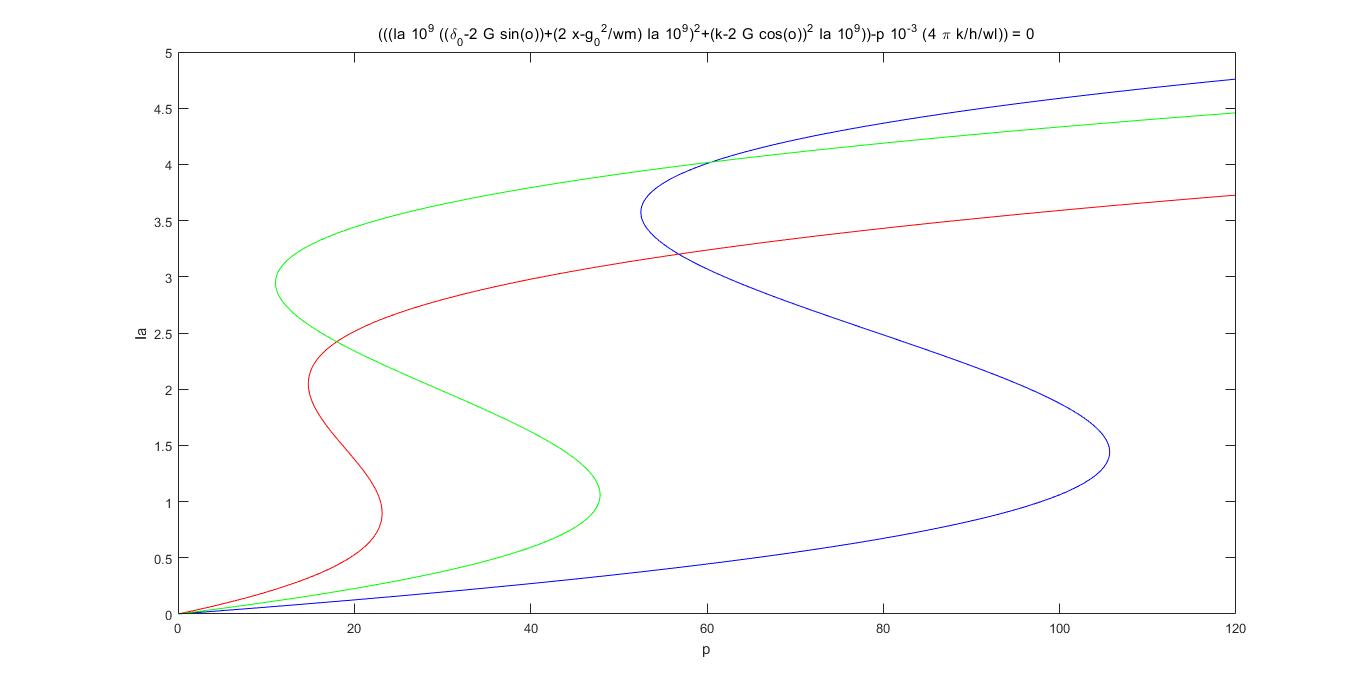
第五章介绍本文的理论模型,对公式进行了推导,并进行图像的仿真,再对可控双稳态现象的结果进行了分析和讨论。
第六章对本文进行了总结,并对未来的发展和工作做了展望。
第2章 光腔力学
2.1 光腔力学的发展背景
光携带的动量会产生辐射压力,开普勒在17世纪就做出了猜想,他注意到彗星的尘埃尾在彗星过境时指向远离太阳的地方(开普勒,1619)。麦克斯韦也预言了辐射压力,第一个明确的实验演示是用了轻型磨机设备完成的(Lebedew,1901年;Nichols和Hull,1901年),然而我们需要对这些实验进行仔细的分析,以区分这一现象与主导早期观测的热效应的区别。早在1909年,爱因斯坦就得出了作用在可移动镜子上的辐射压力偏差的统计数据(爱因斯坦,1909年),包括辐射力的摩擦效应,这一分析使他能够揭示黑体辐射的双波粒子性质。在开创性的实验中,线性和角度宏观物体分别由Frisch(Frisch,1933)和Beth(Beth,1936)证明[3]。
20世纪70年代,阿瑟·阿什金证明聚焦的激光束可用于捕获和控制介电粒子,其中还包括反馈冷却(阿什金,1978年,2006年)。Hänsch和Schawlow以及Dehmelt和Wineland首先指出了辐射压力力的非保守性质及其用于冷却原子运动的可能性(Hänsch和Schawlow, 1975; Wineland和Dehmelt, 1975)。随后在20世纪80年代,激光冷却通过实验而实现,并且成为一项非常重要的技术(Stenholm, 1986),例如,它可以将离子冷却到运动基态,这种离子是超冷原子实验的最基础的素材。许多应用都是通过激光冷却实现的(Metcalf和vanderstraten,1999年),比如说光学原子钟、引力场的精确测量以及原子捕获云中量子多体物理的系统研究(Bloch和Zwerger, 2008)。
Braginsky通过干涉仪研究了辐射压力的作用,以及其为较大物体提供冷却的能力[4-6]。Braginsky考虑了辐射压力对腔体的和谐悬挂端镜的动态影响。他的分析表明,由于有限空腔寿命,力的延迟性质提供了机械运动的阻尼或反阻尼,这是他在使用微波空腔的开创性实验中能够证明的两个影响(Braginsky和Manukin,1967年;Braginsky等人,1970年)。在后来的实验中,人们在KG尺度的微波耦合机械谐振器中观察到了这些现象(Cuthbertson等人,1996)。在光学领域,腔光机实验证明了作用于宏观端镜的辐射压力的双稳态(Dorsel等人,1983年)。
20世纪90年代,量子腔光机系统的理论从几个方面开始了探索[3]。其中包括光的压缩(Fabre等人,1994年;Mancini和Tombesi,1994年)和光强度的量子非破坏性(QND)检测(Jacobs等人,1994年;Pinard等人,1995年),利用光机相互作用产生的有效克尔非线性。对于极强的光机耦合,由此产生的量子非线性可能导致光场和力学的非经典和纠缠态(Bose等人,1997;Mancini等人,1997)。此外,建议通过辐射压力进行反馈冷却(Mancini等人,1998年)。与此同时,一种新的方法被提出:使用腔辅助激光冷却。这是一种冷却缺少闭合内部跃迁的原子和分子运动的方法(Hechenblaikner等人,1998;Vuletic和Chu,2000)[3]。
2.2 光学谐振器
光学谐振器可以在实验中以多种形式实现,在这里,我们给出了光学特性的统一描述,并给出了用单频单色激光源的腔的数学表述。
首先考虑一个最简单的法布里-珀罗谐振器在经典理论下的效应,引入相关参数来表征光学谐振器。法布里-珀罗谐振器由两个反射率极高的反射镜组成,反射镜相距为L,包含一系列由角频率 给出的共振,其中m是整数,两个相邻的共振频率我们定义为自由光谱区:
给出的共振,其中m是整数,两个相邻的共振频率我们定义为自由光谱区:
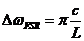 (2.1)
(2.1)
在下面,我们将注意力集中在一个光学模式上,它的频率我们表示为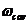 。
。
光学谐振器另一个重要的参量是腔的衰减率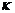 ,
,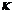 是由两个因素引起的,一是腔镜发射不完全引起的损耗
是由两个因素引起的,一是腔镜发射不完全引起的损耗 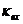 ,这部分损耗是因为镜的吸收、散射以及透射所造成的损耗,通常我们所见的光腔,输出端的反射镜是部分透射的,而另一个反射镜是全反镜,但是其反射率也不可能真正做到百分之百。二是谐振器内部的吸收和外部的散射引起的衰减
,这部分损耗是因为镜的吸收、散射以及透射所造成的损耗,通常我们所见的光腔,输出端的反射镜是部分透射的,而另一个反射镜是全反镜,但是其反射率也不可能真正做到百分之百。二是谐振器内部的吸收和外部的散射引起的衰减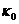 ,这部分主要包括几何偏折损耗、衍射损耗和材料的非激活吸收损耗。光线在腔内来回往返传播时,有可能会从腔的侧边偏转出去,这种损耗我们称之为几何偏折损耗,而由于谐振腔反射镜片的孔径大小是有限的,因此光在镜面上发生衍射时,必然会失去一部分能量,这种损失便是衍射损耗。所以谐振器的总衰减率为
,这部分主要包括几何偏折损耗、衍射损耗和材料的非激活吸收损耗。光线在腔内来回往返传播时,有可能会从腔的侧边偏转出去,这种损耗我们称之为几何偏折损耗,而由于谐振腔反射镜片的孔径大小是有限的,因此光在镜面上发生衍射时,必然会失去一部分能量,这种损失便是衍射损耗。所以谐振器的总衰减率为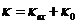 。
。
另一个常用量是光学精细度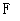 ,它给出了光子离开腔前的平均往返次数:
,它给出了光子离开腔前的平均往返次数:
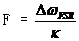 (2.2)
(2.2)
光学精细度是一个用处很广的参数,因为提高它可以提高耦合到谐振器的功率上的循环功率。我们再引入一个量:光学谐振器的品质因数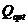
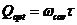 (2.3)
(2.3)
其中,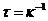 是光子在谐振器中的寿命。
是光子在谐振器中的寿命。
2.3 光腔的输入输出形式
耦合到外部电磁环境的空腔的量子力学描述可以通过内部动力学方程或输入-输出理论框架给出,若是人们还想进一步了解由空腔发出或从中反射而出的光场,输入-输出理论可以帮助我们直接模拟从任何耦合端口(如输入镜)注入到光腔中的量子偏转。此外,它还考虑了可能存在的任何相干激光驱动器。
输入-输出理论是根据海森堡运动方程来制定的,描述了腔内磁场振幅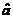 随时间的演化。结果表明,
随时间的演化。结果表明,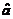 以
以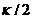 的速率衰减。同时,磁场振幅通过进入腔的各个端口的量子噪声不断对其进行补充。在本例中,我们区分与输入耦合相关的通道的损耗(衰减率
的速率衰减。同时,磁场振幅通过进入腔的各个端口的量子噪声不断对其进行补充。在本例中,我们区分与输入耦合相关的通道的损耗(衰减率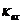 )和其他损耗过程(其他衰减率
)和其他损耗过程(其他衰减率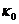 )。运动方程如下:
)。运动方程如下:
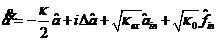 (2.4)
(2.4)
在经典情况下,一个适当归一化的模腔电场复振幅将取代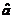 ,事实上,这个方程和下面的方程在经典情况下可以通过简单的取平均值而实现,例如:
,事实上,这个方程和下面的方程在经典情况下可以通过简单的取平均值而实现,例如: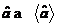 。我们选择了一个以激光频率为
。我们选择了一个以激光频率为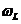 旋转的模型,即在这里
旋转的模型,即在这里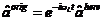 ,并引入了与腔模有关的激光失谐
,并引入了与腔模有关的激光失谐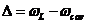 。
。
在这里输入场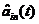 应被视为随机的量子场。在最普遍的情况下,它表示了在时间t时与腔内的偏转真空电场耦合,再加上相干激光驱动。并且,同样的理论也可以用来描述压缩态以及其他更复杂的场态。标准化场的方式如下:
应被视为随机的量子场。在最普遍的情况下,它表示了在时间t时与腔内的偏转真空电场耦合,再加上相干激光驱动。并且,同样的理论也可以用来描述压缩态以及其他更复杂的场态。标准化场的方式如下:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: