表面缺口对镁双晶塑性变形行为的影响毕业论文
2020-02-18 10:05:12
摘 要
镁是一种具有优良力学性能的金属材料,具有比强度高的优良特点,但是其抵抗塑性变形的能力相对较差,这就涉及到镁的强韧化性能的研究。同时在制造过程中会不可避免地产生一些缺陷,如表面缺口。这些缺陷会对镁的塑性变形行为产生一定的影响。本文主要采用分子动力学方法研究表面缺口对镁双晶塑性变形行为的影响。分别建立了表面缺口不在孪晶界处和在孪晶界处的两种纳米柱模型,再施加单向载荷模拟塑性变形过程,对其进行可视化操作后,再对微观结构演化过程进行分析。研究结果表明:表面缺口会阻碍孪晶界的迁移,从而引起塑性阶段的应力波动;表面缺口位置不同,应力-应变曲线的走向趋势不同,这是由B/P界面的形成及孪晶界的迁移共同作用导致的,而且会影响新孪晶的形核。
关键词:表面缺口;分子动力学模拟;孪晶界;塑性变形
Abstract
Magnesium is a metal with excellent mechanical properties, and it has excellent characteristics of high specific strength ,but poor resistance to plastic deformation, this involves the study of the strengthening-toughening properties of magnesium. In addition, certain defects usually occur during the manufacturing process, such as surface notch. These defects may affect the plastic deformation behavior of magnesium. The effect of surface notch on the plastic deformation of magnesium twin crystals was studied by molecular dynamics method. Firstly, two nano-columnar models with a surface notch at different position were established, and then unidirectional loading was applied to simulate the plastic deformation process. After the visualization operation, the microstructure evolution process was analyzed. Simulation results show that the surface notch tends to hinder the migration of the twin boundary, which will cause the stress fluctuation in the plastic stage and affect the nucleation of the new twins. What’s more, different positions of surface notch lead to different trend of stress-strain curve, which is caused by the formation of B/P interface and migration of twin boundary.
Key Words:surface notch;Molecular Dynamic Simulation;twin boundary;plastic deformation
目录
摘要 I
Abstract Ⅱ
第1章 绪论 1
1.1 研究背景 1
1.2 国内外研究现状 1
1.2.1 滑移及孪晶界对镁的力学行为的影响 1
1.2.2 表面缺陷对金属材料力学行为的影响 2
1.3 研究内容 2
第2章 分子动力学模拟 3
2.1 引言 3
2.2 分子体系的运动方程及数值解法 3
2.2.1 分子体系运动方程 3
2.2.2 Verlet算法的改进 4
2.3 边界条件 5
2.3.1 周期性边界条件 5
2.3.2 周期性边界条件的缺点 5
2.4 势函数 6
2.4.1 概述 6
2.4.2 对势 6
2.4.3 多体势 7
第3章 表面缺口不在孪晶界处的镁双晶塑性变形行为研究 8
3.1 引言 8
3.2 建模方法 8
3.3 模拟结果分析与讨论 9
3.3.1 弹性阶段分析 9
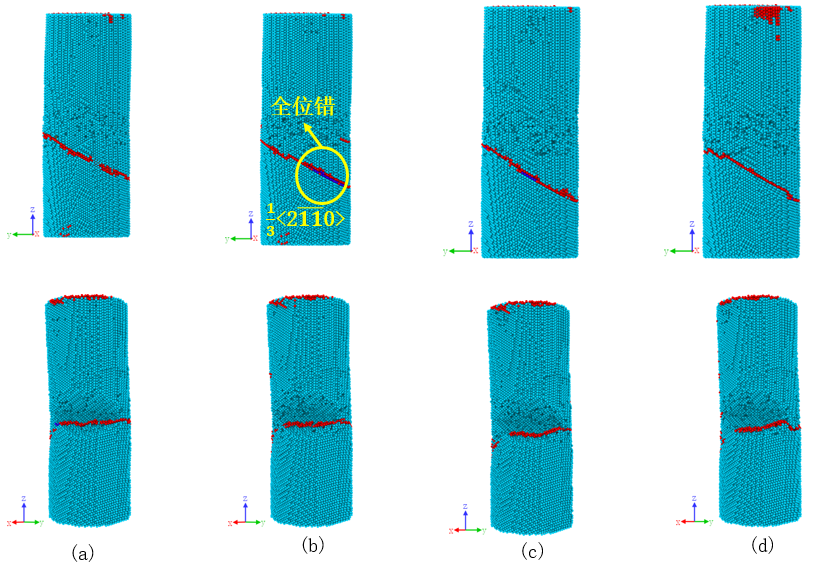
3.3.2 塑性波动阶段分析 10
3.4 本章小结 15
第4章 表面缺口位于孪晶界处的镁双晶塑性变形行为研究 16
4.1 引言 16
4.2 模拟结果分析与讨论 17
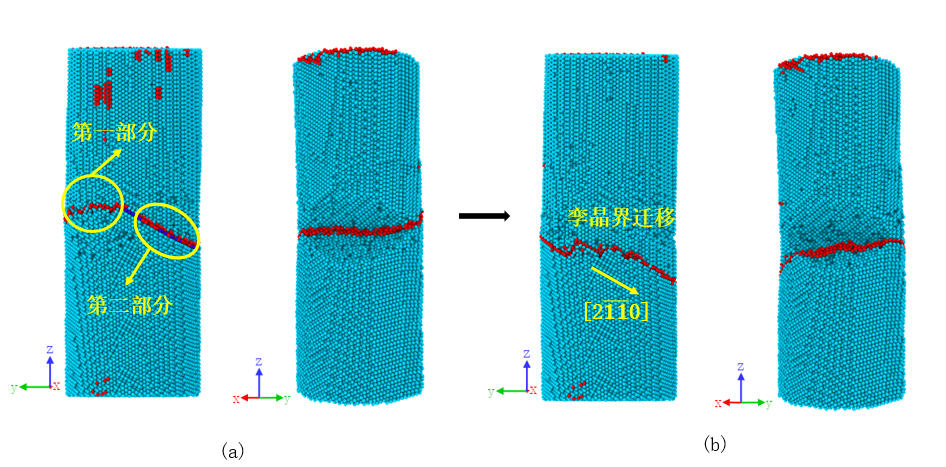
4.2.1 塑性波动阶段分析 17
4.2.2 应力下降阶段分析 20
4.3 本章小结 21
第5章 结论与展望 22
5.1 结论 22
5.2 展望 22
参考文献 23
致谢 25
第1章 绪论
研究背景
镁合金具有比强度高等优良的力学性能、且具有良好的导电导热的物理特性,被广泛应用于机械、电子和抗震等领域。然而,作为一种结构材料,镁合金也有其自身的缺点,如易腐蚀,抗疲劳、抗蠕变能力差等[1]。镁及大部分的镁合金都具有典型的密排六方晶体结构,共有3个独立滑移系。镁合金在宏观上的力学性能表现为塑性变形能力差,在微观尺度上,存在生产或加工过程中所形成的微缺陷[2](缩孔、微裂纹),也对镁合金的宏观力学性能具有一定影响。因此,越来越多的材料和力学研究者从微观尺度着手来分析和研究镁合金[3,4]的宏观性能。分子动力学方法[5,6,7]是近几十年发展起来的一种计算方法,可以解决由大量原子组成的系统的动力学问题。通过计算原子间的相互作用,从微观尺度研究纳米尺度材料内部的缺陷的形成及演化过程,并进一步讨论材料的宏观力学性能。在镁双晶研究方法方面,主要就是从微观尺度观察位错的产生及演变,孪晶界的迁移过程,与应力应变曲线加以对照,研究镁合金的宏观力学性能。随着计算机处理数据能力的提高,我们可以模拟的模型体积也越来越大,模拟结果也更符合宏观规律,这为我们使用分子动力学模拟软件提供了更加可靠的保障。镁合金在制造过程中会出现表面缺口[8,9]和内部缺口两种类型的缺陷,本文拟选择含有表面缺口的镁双晶作为研究对象,通过分子动力学模拟,研究表面缺口类型对镁双晶塑性变形行为的影响,为具有优越力学性能的材料设计工作提供依据。
国内外研究现状
1.2.1 滑移及孪晶界对镁的力学行为的影响
金属的强韧化一直是重要的研究课题,镁金属的强韧性能从微观角度来看与位错滑移及孪生密不可分,徐泓鹭[10]等人通过对带缺口的对称倾斜的晶界的镁的拉伸,得到了两种不同的孪晶,在此基础上分别研究了孪晶界的迁移机制及其稳定性。结果表明,{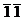 21}孪晶界迁移所需要的能量较少,稳定性差。而{
21}孪晶界迁移所需要的能量较少,稳定性差。而{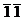 22}孪晶界的迁移主要是由锥面滑移导致的,稳定性较高。在300K温度下,基面滑移与非基面滑移共同作用,协调镁的塑形变形,且在此温度下孪晶界较容易发生迁移。Koike等人[11]研究了镁合金表面台阶形成与孪晶变形的关系,在室温拉伸下,镁合金轧件沿轧制方向发生了变形。在裂缝边缘附近观察到大量的表面台阶。透射电镜显示在这些步骤下存在双晶。认为基体位错滑移在孪晶内部高度活跃。双晶[12,13]内部的局部变形可导致类裂纹断裂的形成,宏观上表现为脆性破坏。但是没有具体揭示表面缺口对镁双晶变形的影响,因此在研究材料的塑性变形行为时,有必要综合考虑表面缺陷与孪晶界的影响。
22}孪晶界的迁移主要是由锥面滑移导致的,稳定性较高。在300K温度下,基面滑移与非基面滑移共同作用,协调镁的塑形变形,且在此温度下孪晶界较容易发生迁移。Koike等人[11]研究了镁合金表面台阶形成与孪晶变形的关系,在室温拉伸下,镁合金轧件沿轧制方向发生了变形。在裂缝边缘附近观察到大量的表面台阶。透射电镜显示在这些步骤下存在双晶。认为基体位错滑移在孪晶内部高度活跃。双晶[12,13]内部的局部变形可导致类裂纹断裂的形成,宏观上表现为脆性破坏。但是没有具体揭示表面缺口对镁双晶变形的影响,因此在研究材料的塑性变形行为时,有必要综合考虑表面缺陷与孪晶界的影响。
1.2.2 表面缺陷对金属材料力学行为的影响
表面缺口会对材料的力学性能产生很大影响,Wu等人[14]研究了含表面缺陷和不含表面缺陷的γ-TiAl拉伸变形和断裂的分子动力学模拟,结果得出:脆性断裂发生在完好体中;表面和边缘的缺陷会破坏材料的强度,并提供位错形核的位置。表面和边缘的缺陷会导致进一步的弱化,随着缺陷类型、尺寸、位置和方向的不同,会产生不同的影响,其中边缘缺口的影响最大。当表面缺口很小时,从γ-TiAl棒的边缘会产生位错,只有当缺口大于依赖于临界尺寸的应变速率时,才会发生位错成核的现象。表面划痕的影响是定向的和而且对形状敏感。平行于加载方向的划痕影响不大,垂直于加载方向的划痕锋利尖锐,易造成裂纹,应避免。该模拟还表明,任何类型的表面缺陷都会降低强度,并在某些情况下导致裂纹。但如果控制得当,可能会促进位错成核,提高组织的延展性。但这是针对TiAl的研究,镁的性质偏脆,需要单独进行分子动力学模拟。在关于镁的缺陷研究中,曾祥国等人[15]对顶端带有裂纹的镁合金模型进行了分子动力学模拟,研究发现,裂纹的扩展是一个十分复杂的过程,裂纹类型会对裂纹的扩展以及位错的形成产生影响,尖裂纹扩展时,主裂纹附近会产生大量的副裂纹,副裂纹快速扩展,最终与主裂纹连接在一起,并伴有滑移系的位错发射,揭示了缺陷与位错发射之间的关系。但是该研究只是对裂纹扩展过程的研究,没有加入孪晶界,没能揭示缺陷与孪晶界的相互作用。
研究内容
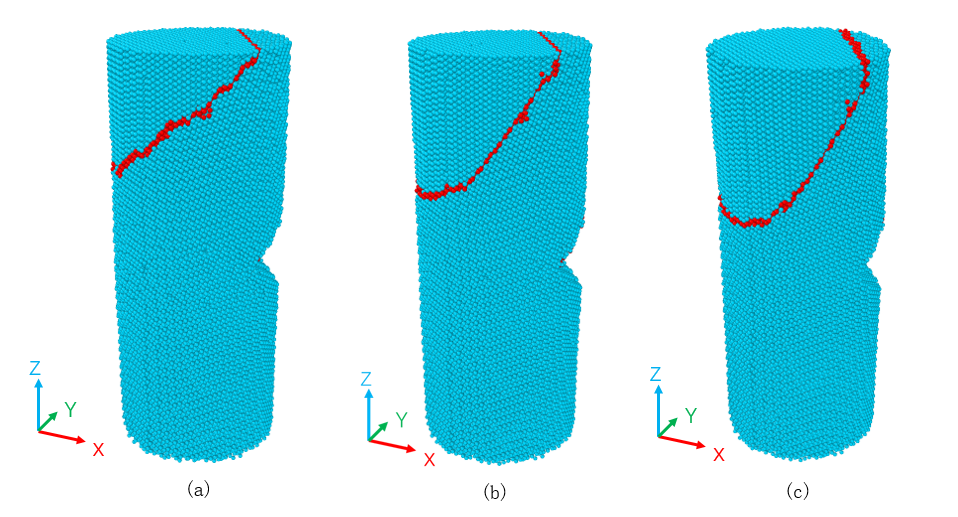
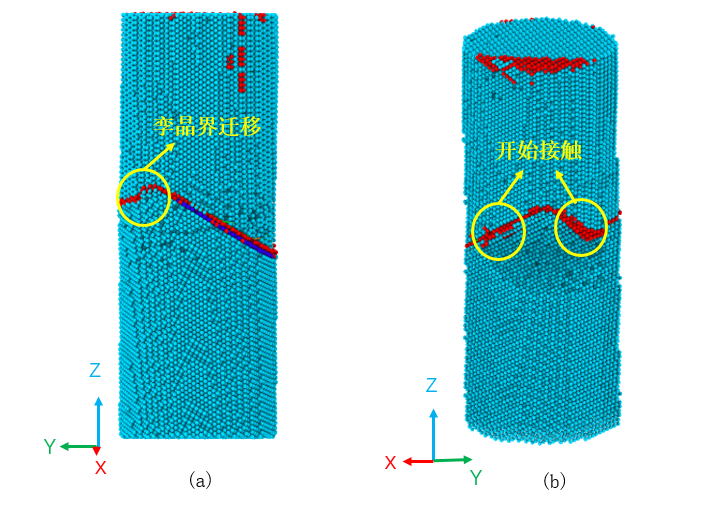
本文采用LAMMPS开展工作,首先建立不含表面缺口的镁双晶模型,进行单轴压缩,观察镁双晶微观模型的变化,判断镁双晶模型建立的正确性。再建立含有表面缺口的镁双晶模型,缺口位置分别位于孪晶界上和非孪晶界上,以同样的应变速率单轴拉伸,分别考察应力-应变曲线和微观原子结构图,研究表面缺口对镁双晶强度及塑性的影响。
第2章 分子动力学模拟
2.1 引言
分子动力学模拟包括分子力学(MM),蒙特卡罗(MC)模拟,分子动力学(MD)模拟[16]。其中分子动力学模拟通过建立一组分子(或原子)的运动方程,然后计算系统中的每个分子运动方程的数值解,得到各个时刻下每个分子的坐标与能量数据,从而可以得到各个分子的运动规律,再通过数学统计的方法得到模型的宏观力学性质。分子动力学模拟根据物理及化学原理,通过由模拟计算代替实验测算的研究方式,得到相关的材料性能参数。不仅能得到具体的原子运动细节,还能根据自己需要加入实验限制条件,通过具体工具观察到模型的变化过程。分子动力学模拟不仅能够用来研究材料的内外部结构,计算材料具有的性质,还能预测材料的力学行为,此外,还可以验证,重现实验过程,从微观角度认识材料。分子动力学模拟与传统实验相比,可以降低实验成本,具有更高的安全性,可以实现通常条件下无法完成的实验,比如超高温条件与超低温实验。理论模拟与具体实验相比,精确度要求是模拟首要考虑的问题,所以能够模拟更大的体系,具有更高的模拟效率,可以取得更高的精确度是分子动力学的发展趋势。运动方程的数值求解,边界条件的选用,势函数[17]的构造以及系综[18]的选择都会影响到最后的模拟结果。
2.2 分子体系的运动方程及数值解法
2.2.1 分子体系运动方程
分子体系的运动可以简化为组成分子体系的原子的相互作用,原子的质量主要集中在原子核,因此可以视为简单的质点运动体系。由牛顿运动第二定律,分子体系的各个方向上的运动方程可以写为:
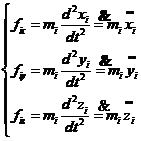 (2.1)
(2.1)

式中:i为原子序号,(fix,fix,fix)为各个原子所受分力,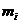 为各个原子的相对原子质量,(
为各个原子的相对原子质量,(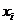 ,
,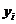 ,
,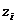 )为各个原子的位置坐标,()为坐标的关于时间的二阶导数。还可以用矢量表示为:
)为各个原子的位置坐标,()为坐标的关于时间的二阶导数。还可以用矢量表示为:
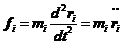 (2.2)
(2.2)
式中: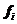 为受力矢,
为受力矢,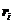 量为坐标矢量,
量为坐标矢量,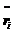 为坐标关于时间的二阶导。
为坐标关于时间的二阶导。
2.2.2 Verlet算法的改进
分子体系的相互作用非常复杂,很难解出解析解,只能采用差分法得到方程的近似数值解。比较经典的有Euler算法,Verlet算法,蛙跳算法及速度Verlet算法。其中Euler算法采用向前差分公式,精度较低,且限制了时间步长,效率不高。Verlet算法是Euler算法的改进,位置计算精度由一阶提高至四阶,但精度可能会随着计算过程推进逐渐降低,而且求解速度时需要先得到位置,故速度精度只有二阶。为了克服这些缺点,产生了Verlet算法的改进算法:蛙跳法和速度Verlet算法。
先来简单介绍一下Verlet算法:
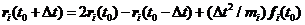 (2.3)
(2.3)
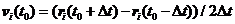 (2.4)
(2.4)
计算时,先由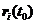 得到
得到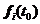 ,再由前一步的位置
,再由前一步的位置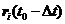 计算得到后一步的位置
计算得到后一步的位置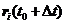 ,然后由
,然后由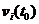 公式得到
公式得到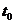 时刻的速度。
时刻的速度。
蛙跳算法作为改进,差分公式变为:
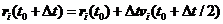 (2.5)
(2.5)
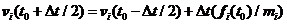 (2.6)
(2.6)
由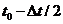 时刻的速度和
时刻的速度和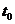 时刻的加速度,得到
时刻的加速度,得到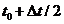 时刻的速度,接着利用
时刻的速度,接着利用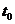 时刻的位置得到
时刻的位置得到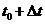 时刻的位置,
时刻的位置,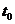 时刻的速度由速度公式计算:
时刻的速度由速度公式计算:
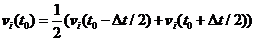 (2.7)
(2.7)
即在速度计算时跳过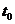 时刻,直接由相关的加速度信息及
时刻,直接由相关的加速度信息及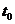 前的某一时刻的速度得到
前的某一时刻的速度得到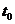 后某一时刻的速度。这样,蛙跳算法就避免了大数相减,减小了误差,速度的计算精度与位置计算精度相同,同为四阶。但存在着速度计算和位置计算不同步的问题,不能在同一时刻分别由速度和位置得到动能和势能。
后某一时刻的速度。这样,蛙跳算法就避免了大数相减,减小了误差,速度的计算精度与位置计算精度相同,同为四阶。但存在着速度计算和位置计算不同步的问题,不能在同一时刻分别由速度和位置得到动能和势能。
速度Verlet算法是Verlet算法的另一种改良算法,差分公式为:
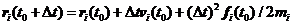 (2.8)
(2.8)
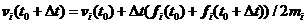 (2.9)
(2.9)
在知道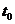 时刻的分子坐标后,可以方便得到该时刻的速度和受力大小及方向,再由差分公式可以计算得到
时刻的分子坐标后,可以方便得到该时刻的速度和受力大小及方向,再由差分公式可以计算得到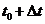 时刻的位置坐标,速度及受力。优点在于不仅提高了精确度,而且可以同时得到位置坐标和速度,是现在应用比较广泛的一种算法。
时刻的位置坐标,速度及受力。优点在于不仅提高了精确度,而且可以同时得到位置坐标和速度,是现在应用比较广泛的一种算法。
2.3 边界条件
2.3.1 周期性边界条件
基于现在的计算机发展水平,对完整的宏观物体进行分子动力学模拟是不现实的,计算机CPU无法处理这么庞大的数据,所以只能用几千或者上万的原子代替进行纳米尺度的微观模型分析。而且体系内部与表面的作用情况是不一样的,为了消除表面效应的影响,引入了周期性边界条件,使模拟体系成为具有同样性质的宏观物体的一部分。基本原理是首先建立一个中心元胞,重复复制这个元胞,使这种元胞规律地地出现在三维空间的各处。这样整个模拟区域就变得无限大,接近宏观物体。
中心元胞种的每个粒子通过笛卡尔坐标系确定位置,设原始元胞中任意一个粒子的位置坐标为(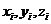 ),这样复制的像粒子位置坐标为:
),这样复制的像粒子位置坐标为:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: