基于CVaR模型的证券市场实证研究毕业论文
2020-03-08 10:12:16
摘 要
收益与风险总是相伴而生,理性的投资者则是在可承受的风险水平之下追求获得最大化的收益。投资组合理论可以帮助投资者在获得既定收益的同时又达到分散风险的目的。经典的均值-方差理论是投资组合理论的基础,其他的投资组合理论大多是在其基础上演变而来。
在风险度量方面,近些年VaR风险度量方法与CVaR风险度量方法被广泛使用。本文通过对这些风险度量方法的演进过程进行系统介绍和分析,最终以CVaR风险度量方法为落脚点,结合均值-方差理论构造了均值-CVaR模型,着重分析了均值-CVaR模型的原理和计算方法,并结合现实的约束条件探究均值-CVaR优化模型。
本文采用历史模拟法,选取了13支不同行业的股票对上述模型进行实证研究,验证了均值- CVaR模型在我国证券市场中具有良好的适用性。
关键词:投资组合;风险度量;CVaR
Abstract
Returns and risks always come together, but rational investors are pursuing the maximum benefits under the level of affordable risk. Portfolio theory can help investors achieve the purpose of dispersing risk while achieving a given return. Classical mean-variance theory is the foundation of portfolio theory. Other portfolio theories are mostly evolved on the basis of it.
In terms of risk measurement, VaR risk measurement methods and CVaR risk measurement methods have been widely used in recent years. This paper systematically introduces and analyzes the evolution process of these risk measurement methods, and finally takes the CVaR risk measurement method as the ultimate result, combines the mean-variance theory with construct the mean-CVaR model, and focuses on the analysis of the principle and calculation method of the mean-CVaR model, and explores the mean-CVaR optimization model according to the constraints of reality.
This paper adopts the historical simulation method and selects 13 stocks from different industries to conduct empirical research on the above model, which verifies that the mean-CVaR model has good applicability in China's securities market.
Key Words:portfolio theory;risk measurement;CVaR
目录
第一章 引言 1
1.1 研究背景和意义 1
1.2 国内外研究现状 1
1.3 研究方法 2
第2章 证券市场风险度量方法 3
2.1 经典投资组合M-V模型 3
2.2 VaR风险度量方法 4
2.2.1 VaR的概念 4
2.2.2 VaR的计算方法 4
第3章 基于CVaR的投资组合优化模型 7
3.1 CVaR度量方法 7
3.1.1 CVaR的定义及性质 7
3.1.2 CVaR的计算方法 8
3.2均值-CVaR投资组合优化模型 9
3.2.1 构建均值-CVaR模型 9
3.2.2 正态分布条件下均值-CVaR模型的有效前沿 11
3.2.3 考虑交易成本的均值-CVaR优化模型 11
第4章 模型的实证研究 14
4.1 数据选择及处理 14
4.2 计算及结果分析 15
4.2.1 均值-方差与均值-CVaR比较 18
4.2.2 考虑交易成本对均值-CVaR的影响 20
4.3 模型在我国应用中存在的问题及改进意见 23
第5章 结论与展望 24
5.1 结论 24
5.2 展望 24
参考文献 25
致谢 27
第一章 引言
1.1 研究背景和意义
从1990年第一个证券交易所——深交所成立至今,短短二三十年的时间,我国的资本市场经历了从弱小到逐渐壮大的发展过程。当前阶段,我国已经进入了改革开放的攻坚期,经济发展也由高速增长慢慢转向高质量发展。十九大报告中讲到,我们要着力加快建设实体经济、科技创新、现代金融协同发展的产业体系,着力构建市场机制有效、微观主体有活力、宏观调控有度的经济体制。
在经济发展的大背景下,资产投资也逐渐进入人们的视野,成为生活必不可少的一部分。我们假设活跃在证券市场中的投资者都是理性的经济人,都以追求效用最大化为目标,那么收益和风险这一对矛盾就是每个投资者无法避免的问题。投资组合理论给了投资者一个良好的选择。投资组合是指投资者或机构所持有的股票、债券、衍生金融产品所构成的集合。投资者或基金经理按照资产选择理论和投资组合理论对投资组合进行管理,从而达到分散风险、提高收益的目的。
对于投资机构而言,因为风险是金融市场的基本属性之一,任何投资机构都无法完全规避。因而如何进行风险管理是各类金融机构业务管理中最核心的内容,风险管理的有效性也是金融机构能否在纷繁复杂的金融市场中具有竞争力的关键因素之一。而风险管理最重要也是最基础的步骤就是进行风险的量化,这也就意味着,选取可靠的金融风险度量方法,对于资源配置的最优化、投资者投资收益的最大化有着至关重要的意义[1]。
1.2 国内外研究现状
1952年,Markowitz发表了题为Portfolio Selection的文章,在文中将方差作为基本风险度量工具提出了投资组合的均值—方差模型[2]。1963年,Baumol W提出了VaR风险度量指标的雏形,他认为VaR是指在正常的市场环境中,在设定的某种置信水平下和持有期内,我们衡量的某个特定的投资头寸或组合所面临的最大可能损失。20世纪90年代,JPMorgan公司再次提出了VaR风险度量指标。实际上, VaR风险度量指标提出之后,就被广泛用于度量证券交易的市场风险。尽管VaR风险度量方法被广泛的应用于证券市场当中,但VaR风险度量方法存在着一定的缺陷。VaR只考虑了设定的最大预期损失,但没有考虑超过设定损失的小概率事件,因而不能反映金融市场上的极端事件;VaR也不满足一致性风险度量模型的次可加性,因此基于VaR风险度量方法的投资组合优化模型可能会存在这多个极值,我们求出的最优解可能只是局部最优解。于是,在这种背景下,由Rochafellar和Uryasev两人提出的CVaR风险度量方法因为具有良好的统计性质,并且基于CVaR风险度量方法的模型便于求解而逐渐被人关注[3]。
1999年 Rockafeller和Uryasev发表了题为Optimization of Conditional Value at Risk的文章,文中首次提到了CVaR的概念,分析了CVaR的性质,并且推导出了在正态分布条件下的计算公式和投资优化模型[4]。之后,Jonas Palmquist, Uryasev和Pavlo Krokhamal在之前的研究基础之上,推导出了在正态分布条件下均值-CVaR模型的有效前沿,并分析了基于均值-CVaR模型的投资优化问题[5]。后来Rflung对VaR、CVaR两种方法的定义、实质、性质等方面进行了系统的比对[6]。
在国内的研究方面,1997年,牛昂率先在国内研究了VaR风险度量方法,他简单介绍了VaR风险度量方法的定义和在国际上的应用。进入21世纪之后,国内学者对于VaR风险度量方法的研究开始侧重于实践,主要研究的方向是深证指数的风险以及在肥尾分布条件下的投资组合优化问题等。2002年,陈金龙学者在国内首先介绍了 CVaR模型的基本概念和基本的计算方法[7]。之后,国内的学者对VaR风险度量方法和 CVaR风险度量方法进行了比较:司继文学者和王秀国学者分别利用蒙特卡洛模拟法证实了CVaR风险度量方法在实际应用和贷款组合中的优越性;王慧敏等学者运用极值理论研究两种度量方法的计算,并运用两种方法对债券组合进行优化[8]。
1.3 研究方法
通过上述国内外研究现状,我们可以得知当前对度量金融风险的研究更加侧重于VaR方法,但由于VaR度量指标的局限性,未来CVaR将会取代VaR成为主流度量指标。因此,本文在上述投资组合和风险度量的理论基础上对CVaR模型进行深入地研究,并选取13支股票对研究的结论在国内的适用性进行实证分析。
文章全文共分为四章。第一章主要介绍了本文的研究背景和研究意义,并阐述了国内外的研究现状以及本文的研究方法。第二章主要介绍证券投资风险管理的方法,经典的MV模型,VaR的基本概念、计算方法并分析了VaR风险度量方法的缺陷。第三章的主要内容是CVaR方法的定义、性质,构建均值-CVaR模型,考虑含有交易成本下的CVaR模型,并求解出其有效前沿。第四章在第三章的理论基础上,选取13支股票的历史数据进行实证分析。在此过程中运用Excel、MATLAB等工具来计算收益率等数据,调用MATLAB指令来求解模型,并运用Origin等专业绘图软件作图,辅助分析。最后讨论了在CVaR应用研究中的一些问题,并提出了一些改进方法。
第2章 证券市场风险度量方法
William F. Sharpe在Investments一书中将风险定义为受损失的可能性。在证券市场中,证券市场风险是指由于各种不确定因素而导致证券价格发生非正常波动,从而给市场参与者造成损失的可能性。随着学者研究的逐渐深入,证券市场的风险度量方法也在不断发展。目前,常用的证券市场风险的度量方法主要包括均值-方差分析、灵敏度分析、波动性方法以及VaR与CVaR等方法。
2.1 经典投资组合M-V模型
Markowitz于1952年发表了Portfolio Selection一文,说明了通过分散投资的方式来降低投资风险的原因,并提出了以方差为投资组合风险度量目标的均值-方差模型[9]。文中为我们建立了一个选择投资组合的通识原则,即投资者可以在已经确定的收益水平下选择风险最小的组合,也可以在相同的风险水平下选择收益最高的组合。之后,Markowitz利用一系列假设来简化问题,达到解决优化问题的目的。主要假设为:
- 假定投资者是追求高收益低风险的理性人。
- 假设证券的价格正确的反映了证券的价值。
- 假设资产收益率服从正态分布,且各资产之间的收益率具有一定的相关性。
在上述假设的条件下Markowitz建立了著名的均值-方差模型。
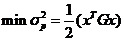
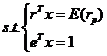 (2.1)
(2.1)
式中,
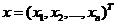 表示投资组合中各资产所占比例
表示投资组合中各资产所占比例
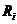 表示第
表示第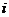 种资产的收益率(随机变量),资产收益率的均值
种资产的收益率(随机变量),资产收益率的均值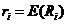 ,其中
,其中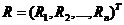 ,
,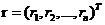
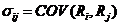 ,
,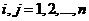
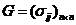 表示n种资产间的协方差矩阵
表示n种资产间的协方差矩阵
根据上述模型我们可以计算出投资组合的期望收益率和标准差的关系如下:
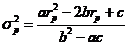 (2.2)
(2.2)
其中,
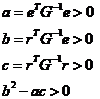
模型(2.1)是在允许卖空条件下建立的,在不允许卖空时还需要加上每种资产的投资比例非负这个约束条件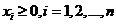
2.2 VaR风险度量方法
2.2.1 VaR的概念
VaR(Value at Risk, 简称VaR),被译为风险资产价值,也被称为受险价值、在险价值。是指在市场正常波动下,金融资产或证券组合的最大可能损失。更为确切的说,是指在一定的置信度下,金融资产或证券组合价值在未来特定时期内的最大潜在损失[10]。
VaR用数学公式可以表示为:
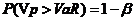 (2.3)
(2.3)
其中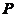 为资产价值的损失大于设定的最大损失的概率,
为资产价值的损失大于设定的最大损失的概率,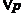 为资产在持有期内的损失,
为资产在持有期内的损失, 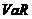 为设定的置信水平下
为设定的置信水平下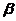 下最大损失。通过公式(2.3)我们就可以把面临的风险量化成为具体的VaR值来帮助投资者做决策。
下最大损失。通过公式(2.3)我们就可以把面临的风险量化成为具体的VaR值来帮助投资者做决策。
用一个实例说明VaR值的现实意义。假设我们所持有的资产在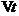 的时间里,在置信水平为95%时计算得到的VaR值为200万。这也就意味着,在未来
的时间里,在置信水平为95%时计算得到的VaR值为200万。这也就意味着,在未来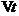 的时间里由于市场波动我们的最大损失超过200万的可能性为5%。
的时间里由于市场波动我们的最大损失超过200万的可能性为5%。
2.2.2 VaR的计算方法
从式(2.3)中可以看出有两个重要的外部因素会影响VaR的大小:持有期、置信水平。在本文中因为主要目的是寻求最优的投资组合,我们假设这两个因素都保持不变。假设持有期为1天,即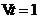 ;置信水平为95%保持不变。
;置信水平为95%保持不变。
为了方便下文描述,统一符号的经济含义。资产组合的初始价值为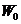 ,持有期的预期收益为
,持有期的预期收益为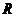 (
(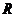 的期望为
的期望为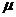 、标准差为
、标准差为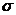 ),给定的置信水平为
),给定的置信水平为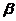 。持有期末资产组合的最低价值用公式可以表示为
。持有期末资产组合的最低价值用公式可以表示为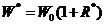 ,其中
,其中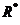 为最低收益率(一般为负值)。因此,在正态分布下VaR的表达式应为:
为最低收益率(一般为负值)。因此,在正态分布下VaR的表达式应为:
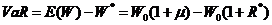
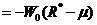 (2.4)
(2.4)
VaR也可以通过投资组合价值的概率分布推导得出,我们通过VaR的定义可知:
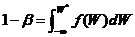 (2.5)
(2.5)
即投资组合的价值低于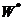 的概率为
的概率为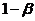 ,因为VaR要求投资组合的价值服从正态分布,我们假定
,因为VaR要求投资组合的价值服从正态分布,我们假定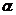 为标准正态分布下的分位点,则有:
为标准正态分布下的分位点,则有:
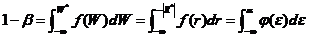 (2.6)
(2.6)




