均值—下半方差证券投资组合模型的实证研究毕业论文
2020-02-22 20:39:09
摘 要
1952年,马科维茨提出了著名的资产组合理论,以均值——方差为核心主张通过多元投资来分散风险。经过不断的研究探讨,经济学家结合投资者心理,将原模型进一步发展为了更加贴合实际地均值——下半方差模型。本文以我国股票投资市场收益率数据为研究样本,从对比收益率的角度出发,证明了改动后模型的优越性,并根据分析影响因素,得出了预设方差和收益率之间的正相关关系,以及股票数量对模型优越性的不确定性影响。通过进一步规划求解,发现了相关数据和收益率差之间的负相关关系。
本文在研究视角、研究内容及指标设计等方面有一定的创新性。本文数据来源于股票市场各行业板块,涵盖多个领域,以季度收益率为样本,具有稳定性。同时进行了多重对比,努力消除现有因素对结果生成的影响,能为学术界提供一个较好的研究参考,也对投资者合理分散风险,进而更好地获取收益有着重要的实践意义。
关键词:均值——方差;均值——下半方差;收益率
Abstract
In 1952, Markowitz put forward the famous theory of asset portfolio and advocated multivariate investment to eliminate risk with the mean-variance as the core. In the long-term research and discussion, economists combined investor psychology and further developed the original model into the mean-semi- variance model, which is more in line with our reality. This paper takes China's stock investment market data as a research sample, compares the profitability point of view, and proves the superiority of the modified model. Based on the analysis of influencing factors, a positive correlation between preset variance and yield is obtained as well as the influence of the number of stocks on the uncertainty of the superiority of the model. Through further planning and solving, we found a negative correlation between related data and profitability.
This article has a certain degree of innovation in terms of research perspective, content, and indicator design. The data in this paper is derived from various sectors of the stock market ,covering multiple sectors.With quarterly returns as a sample, they can be more stable. At the same time, we conducted multiple comparisons and worked hard to eliminate the impact of existing factors on the outcomes. This can provide a good research reference for the academic community, and it also has important practical significance for investors to reasonably distribute risks and better obtain returns.
Key Words: mean-variance; mean-semi- variance model;preset variance;the number of stocks
目 录
第一章 引言 1
1.1研究背景 1
1.2国内外研究现状 2
1.3研究意义 3
1.3.1理论意义 3
1.3.2现实意义 3
1.3.3创新点 3
1.4研究内容框架及方法 4
1.4.1研究内容及框架 4
1.4.2研究方法 4
第二章 相关定理介绍 6
3.1均值——方差理论 6
2.1.1收益和风险 7
2.1.2均值——方差理论模型 8
2.1.3均值——下半方差理论模型 9
2.2模型解释 10
第3章 实证研究 11
3.1模型优越性 11
3.2模型优越性的影响因素 14
3.2.1规定的预设方差对模型优越性的影响 14
3.2.2 股票数量对模型优越性的影响 18
第4章 实证总结 22
第5章 本文局限与研究展望 24
参考文献 25
致谢 27
均值—下半方差证券投资组合模型的实证研究
第1章 引言
1.1研究背景
1952年,Markowitz在《金融杂志》上发表了著名的经济论文——《证券组合选择》,将最佳的投资组合定义为具有风险厌恶特征的投资者的无差异曲线和资产的有效边界线的交点,并突破性地将概率论和线性代数的方法应用于证券投资组合研究中,深入探讨了不同类别、运动方向各异的证券资产之间的内在相关性。1959年,《证券组合选择》出版,以多元投资为出发点详细论述了证券组合的基本原理,为现代西方证券投资理论奠定了基础,标志了现代证券组合理论的开端,大大促进了西方经济学的发展。
均值—方差理论作为资产组合理论的重要内容,以资产自身均值表现未来收益率,以其方差衡量潜在风险,提出投资者在进行投资时,不仅会考虑期望收益率最大,也会考虑风险方差最小,并针对他们厌恶风险的理性化特征,以最小方差下的投资约束证明了“高风险,高收益”的不确定性资产的本质特征——收益是对风险的补偿,证明了分散投资的优点,给予了投资者一定的衡量法则,具有很强的实践性与应用性。经过半个世纪的发展,已经取得了丰富成果,在实践中也被广泛应用。
但是,随着研究的深入,该模型的缺陷也逐渐暴露。实际操作中,投资者在期末清点得失时,一般会得到有收益和有亏损两种结果,这也可以理解为是正风险和负风险两种不同的表现形式。均值——方差理论认为只要偏离了期望收益率,就会造成风险,都应纳入考量之中。事实上,在真实的投资活动中,人们对于风险的真实定义常常与以上不同,即只有当实际收益率低于预期收益率时,相应部分投资才算是有风险的投资,这样的亏损才常常被认为是一种风险,对于投资者的投资影响也是最明显的。这和学术上对于风险是指所有收益率偏离中心收益率的程度的解释不同,可以说前者只是后者的一部分。因此,为了更加符合投资者的投资行为与策略实际,拓展资产组合理论的适用性和全面性,经济学家在传统的均值-方差理论模型之上,又提出了均值——下半方差理论,用半方差代替方差,只将实际收益率低于预期收益率的部分纳入风险测量与分析之中。这样,投资者在决策时只需考虑当有亏损时,即失败的结果,而不用将未承受损失的投资也进行考虑,以便简化投资决策的过程与时间,优化投资格局,有的放矢,符合现代社会对高效率的客观要求。
1.2国内外研究现状
十九世纪五十年代,现代金融理论对于投资多元化的研究才逐渐拉开序幕。Markowitz在1952年最早提出以数量模式来衡量组合的风险与收益,提出理性的投资者在进行投资决策时,会将收益和风险都纳入考虑范围,并创造性地提出了用目标资产的方差来代表其风险,通过资产的收益偏离度来衡量其不稳定性,并在此基础上建立了著名的均值-方差模型。当然,此模型有一个非常重要的假设前提条件:进行投资决策的投资者都具有理性思维,即在相同的投资收益下,投资者会更偏向于具有最低投资风险的资产组合;而如果是相同的投资风险,他们会追求最高的收益。为了达到这个目的,投资者常常需要做到不把鸡蛋放到一个篮子中。1988年,William Sharpe经过长期研究指出,资产配置在投资决策中占据着极其重要的位置。因为有因总体股价变动而影响资产价格变化的系统性风险的存在,所以投资者在投资于任何一种有价证券时,风险都是无法完全避免的,即一定风险的存在是必然的。由此,影响资产股价的某些特殊要素引起的价格变动,即非系统性风险的消除问题,越发受到经济学家的重视。Brinson 、Hood和Beebower在1986年的研究也证明,资产配置几乎可以决定该投资组合收益方差的91.5%。因此,虽然投资的多样化只能消除非系统风险,并不能消除系统风险,但对于投资者来说,合理的资产分配也能很大程度上帮助他们规避许多潜在隐患,增强资产的自身抗风险性。自此,投资管理界经历了翻天覆地的变化,马科维茨的投资组合理论以及由它引导出的资本资产定价模型(CAPM)在学术界与业界的影响极其深远,如今已成为绝大多数理性的投资人都会纳入参考的最重要的方法,
如今,资产配置在投资决策中的重要地位已逐渐被投资者所重视和认可,国际学者的研究也表明资产配置在投资收益方面具有决定性的作用。但随着研究的深入和投资市场的深化,关于均值——方差模型存在的弊端,在国内外也引发了许多人的讨论。后人在均值方差模型的基础上,也做出了不同程度的改进。
首先是庞大的计算量。在均值—方差模型中,需要计算可供选择的资产间的协方差,假设有M种可供选择的资产,则需估计M(M-1)/2个相关系数。当变量M很大时,证券之间的协方差的计算量也会非常庞大,在很大程度上影响和限制了此模型的适用程度。因此,William Sharpe和Lintner分别在1964年和1965年引入了无风险资产,建立了单因素模型,进而推导出资本资产定价模型(CAPM),简化了计算程序。
其次,在进行资产决策时,投资者的心理认知对资产选择的影响也越来越受到关注,由此引发了方差是否是用来衡量证券风险的合理性参数的讨论。马科维茨的假设条件中,方差代表有价资产价值的波动情况,体现其相对于期望收益率的离散程度。但在现实生活中,在投资者心中,证券价格的上浮并不是他们所不愿意看到的。实际上,他们并不将之归为风险,真正让投资者担心的,是投资结果中出现的亏损,即下沉风险,此时证券价格低于预期收益。放在初始的模型中,如果用方差表示投资风险,则既包括下行风险,也包括上行风险,不仅违背投资者心理,也留下了大量的计算作业。1959年,Markowitz在研究中发现,下行风险衡量法更加贴合实际应用,提出了改进的均值——方差模型,即均值——下半方差模型。它将证券产品低于预期收益率的部分纳入风险考量中,而不考虑其收益或价值不变的部分。在顺应投资者心理的同时,减少了计算量,提高了应用效率。
我国学者在投资组合选择理论研究上也取得了一些高水平的研究成果,特别是在动态均值—方差分析方面,处于国际领先地位。但在实践方面,我国几乎还处在起跑线上。
1.3研究意义
1.3.1理论意义
世界经济的不断发展时刻影响着投资者的决策行为,当前经济学家关于投资组合的研究也日益丰富。面对变幻莫测的证券市场和难以捉摸的投资者心理,要想研究结果更加贴合实际,便需要将市场与投资者相结合,以人为本,展开讨论。本文从针对马科维茨均值——方差理论模型计算量大、忽略投资者心理的缺陷而提出的均值——下半方差理论模型入手,探讨了资产风险与收益率之间的关系与平衡。
虽然国内外关于资产风险的研究不在少数,但其中,国外学者多以其本国市场为研究对象,对于我国自身,则缺乏实证性。本文以2015年-2018年起伏不断、跌宕不定的股票市场为背景,从代表性股票数据出发,进行了多重对比,相信会对之前相关问题的研究文献在一定程度上做一个补充。
1.3.2现实意义
本文以真实的股票数据为研究对象,包含多种行业和领域,较为深入地探究了均值——下半方差理论模型在我国证券市场的应用,对指导投资者进行投资决策有着较为普遍的意义。本文的研究有利于指导投资方向,优化投资格局,制定出更科学合理、稳定收益的资金分配方案,完善投资行为,从而使投资者更好地参与投资市场,实现资金价值最大化,同时促进相关企业和市场的发展,增强经济活力。
1.3.3创新点
(1)本文选取的数据背景具有代表性,在包含各行业的前提下,考虑了近三年不断起伏的股票市场,凸显现在经济中考虑风险因子的重要性,强调了投资者心理和其日益理性的投资行为,具有时代性。
(2)本文将所涉及的两种模型进行了多重对比,从均值——下半方差模型的优越性出发,探讨了预设方差和股票数量对投资格局及最后收益率的影响,总结出了一些规律,对投资者投资行为有一定的指导作用。
1.4研究内容框架及方法
1.4.1研究内容及框架
均值-方差理论模型和均值-半方差理论模型涉及的主要对象都是收益率和其对应的方差,只是后者结合了投资者投资的实际情况和他们对于风险的心理认知,从实际收益率低于预期收益率的亏损的数据入手,更有针对性地研究投资决策的产生过程,优化投资格局,获得收益更稳健的投资结果。
本文的基本内容是通过实证研究,从数理的角度探讨预期方差和资产选择数量的的变化对均值——下半方差理论模型优越性的影响。重点讨论资产组合预期方差变化时,对据此形成的投资决策布局及获得的实际收益率的影响,综合应用证券投资市场的具体数据,通过建表立式,同时结合金融报告、专家意见以及投资者心理偏好等来研究证券投资组合的选择问题。研究的目标是通过具体呈现的实证数据,发现并总结出其中的规律,以期得出更多对于证券市场投资决策的启示。
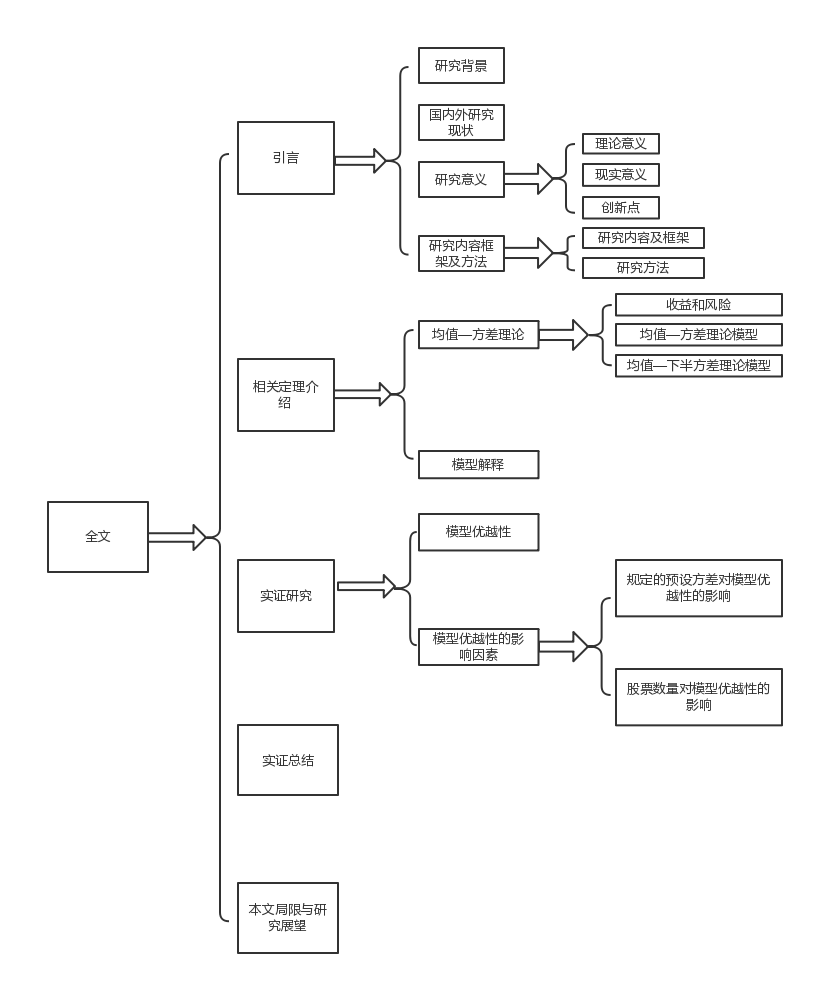
本文首先介绍了均值——方差模型和均值—下半方差模型理论的背景和意义、以及目前在国内外的研究现状和本文研究内容的框架结构。第二章论证了主要模型理论的相关定义,并给出了具体的数理构建,为第三章的实证研究做铺垫。在介绍完相关字母定义和实验顺序后,第三章以证监会行业分类2012版为基准,选取了各行业较活跃的股票各一支,统计它们从2015年3月到2018年3月的每一季度的数据进行实证研究,主要是以收盘价作计算数据,比较两种不同的理论模型下对应的最优投资组合决策,主要体现在收益率上,分析股票数量和预期方差对投资决策的影响。第四章对实证研究得出的结论进行了总结和分析,阐述了均值-方差模型和均值-下半方差模型在实际应用产生的不同结果,并从模型优越性的角度出发,研究改进后的模型优越性的变化。根据文章结果及现有研究进行了总结。第五章对模型的缺陷与不足进行了阐述与假设,并对全文做了最终的总结,对未来研究的发展方向进行了展望。
1.4.2研究方法
本文在查阅大量国内外文献的基础上,计划从实际数据入手,首先设定基本收益率和活跃度标准,从股票投资市场筛选出各行业较优质的符合条件的股票投资产品各一个,共12个。然后为了使数据更加具有稳定性和代表性,以季度划分,避免短时期的波动对股票投资产品的评估,并由此收集不同时期各股票投资产品收益率的具体数据,每个12个,共144个数据,形成具体的数据表格,并应用EXCE中的规划分解、MATLAB进行立式计算,保证数据结果的准确性。最后,建立方差变化下的多重对比,探讨预期变量对于改进后的模型优越性的影响,以期得出一些规律,并进行总结。
同时,在总结单一变量改变下的数据结果的基础上,针对研究方法中的不足进行进一步的分析与解释。
第2章 相关定理介绍
2.1 均值-方差理论
一定时期内,投资者应用自己手中的资金在证券市场进行投资。在期初,他购买一些有价证券,并在期末卖出,期望可以从中获得收益。在这一段时期内,证券的价格会因为总体证券市场价格波动、供求矛盾、社会影响、金融动荡等多方面的因素上下波动,由此会给投资者带来收益或者亏损。当然,在不考虑通货膨胀、交易费等其他支出,只考虑资产本身价格的情况下,也可能没有价格变化;或在考虑了以上硬性支出后仍然与期初投入持平,这是极端情况下的投资结果。但在期初,投资者要考虑的最重要的问题是如何分配手中欲投资的资金,使得自己在期末卖出时的资产组合是最优的,可以达成初始的投资目标。
长期的实践研究表明,理性的投资者在进行投资决策时,并不是简单地选择内在价值最大的证券资产,他们也会关注此类资产自身的收益偏离程度,即价格变动。由于“高风险,高收益”是不确定性资产收益分析的基本特征,投资者在享受一定收益的同时,也要为这种收益承担一定的风险,两者存在正相关的关系。因此,在这一过程中,理性的投资者的决策目标一般有两个:最终尽可能多的收益、投资期中尽可能小的投资风险。由此,为了达成这两个决策目标,投资者常常会拆开手中的资金至两个或两个以上证券产品,以分散自己的投资风险。
马科维茨运用线性规划的方法,将数理统计应用于投资分析,提出了著名的均值-方差理论模型,其基本内容是——为了达到投资者希望的尽可能多的最终收益和尽可能小的投资风险的目标统一,最好的方法是找到这两个相互制约的目标之间的平衡点,或者平衡区间,使得在给定期望收益率的前提下,资产投资者承受的投资方差最小;或在给定预期方差下,资产投资者获取的收益率最大,即在一定范围内达成双向的平衡。该理论依据以下几个假设:
1、投资者在进行每一次资产决策时,是依据特定时期内的证券收益的概率分布,且相关的两个参数——均值、方差(或标准差)。
2、所有资产都存在风险,且投资者是根据证券的实际收益率和期望收益率的偏离程度来估测证券组合的风险。
3、投资者的决定仅仅是依据证券的风险和收益。
4、投资者是理性的投资者,即在一定的风险水平上,投资者期望收益能够最大;相对应的,在一定的收益水平上,投资者希望风险可以最小。
- 所有资产都可以被分成不限数量。
- 不考虑通货膨胀、交易费用、应缴纳税款等因素,即资产组合收益不受市场对它的摩擦。
根据以上假设,马科维茨确立了均值-方差模型,并通过确定证券组合预期收益算法、风险的度量途径和有效边界理论,建立了资产优化配置理论
2.1.1收益和风险




