摘 要

近年来，船舶尤其是承担各种不同任务的远洋运输、科研、资源开采等船舶的多样化发展，船舶运动控制的可靠性与精度的要求也日益增高。随着计算机和信息技术的发展，船舶运动数学模型辨识、船舶航向跟踪预报与控制的可靠性、安全性水平有了进一步的提升。

本文基于最小二乘支持向量机的算法，采用船舶航行实验数据，通过两种方法对某型船只的船舶运动数学模型进行了辨识。证明了参数化模型辨识和非参数化模型辨识的可行性，同时使用辨识所得的模型对船舶航向进行了预报仿真，将预报所得出的航向和实际航向进行对比，证明了两种方法的实用性。并对可能造成误差的因素进行了分析，分析了两种不同方法的优缺点。最后讨论了辨识所得的模型应用于实际船舶控制的可行性。

关键词：船舶航向预测；最小二乘支持向量机；船舶运动数学模型

Abstract

In recent years, the diversified development of ships, especially ocean-going transport, scientific research, and resource exploitation, has taken on various tasks, and the reliability and accuracy of ship motion control have also increased. With the development of computer and information technology, the reliability and safety of the identification of ship movement mathematical model, ship heading tracking and control have been further improved.

In this thesis, based on the least squares support vector machine(LS-SVM) algorithm and the datas of actual ships navigation experiments,the ship movement mathematical model of a certain ship is identified by two methods.The feasibility of parametric model identification and non-parametric model identification is proved. At the same time, using the identified model to simulate the ship's heading, and comparing the heading obtained from the forecast with the actual heading, the practicability of the two methods is proved. The factors that may cause errors are analyzed and the advantages and disadvantages of the two different methods are analyzed. Finally, the feasibility of the identified model applied to the actual ship control is discussed.

Key Words：Ship heading forecast；LS-SVM；mathematical model of Ship movement

目录

第1章 绪论 1

1.1 目的及意义 1

1.2 国内外研究现状 2

1.2.1 船舶操纵发展现状 2

1.2.2 航向控制器的发展现状 2

1.2.3 船舶运动数学模型研究发展现状 3

第二章 船舶运动数学模型 5

2.1 船舶运动数学模型概述 5

2.2 船舶响应模型的建立 6

第三章 支持向量机算法 8

3.1 支持向量机（SVM）综述 8

3.2 支持向量机（SVM）原理 8

3.3 最小二乘支持向量机（LS-SVM）原理 9

3.4 核函数 11

3.5 本章小结 12

第四章 船舶运动数学模型辨识 13

4.1 构造线性响应模型 13

4.2 LSSVM回归分析 15

4.3 基于参数模型的船舶航向预报 16

4.4 误差分析 21

4.4.1 数据测量误差 21

4.4.2 LS-SVM回归中出现的误差 21

4.4.3 响应模型线性化过程中的误差 22

4.5 本章小结 22

第五章 非参数化时序模型辨识 23

5.1 非参数化模型的建立 23

5.2 基于非参数化模型的船舶航向预报 23

5.3 本章小结 25

第六章 总结与展望 26

6.1 经济性分析 26

6.2 环保性分析 26

6.3 总结 26

6.4 展望 27

参考文献 28

致 谢 30

第1章 绪论

1.1 目的及意义

二十世纪下半叶开始，随着国际局势的趋于稳定和两次大战时期积累的技术用于民用航海。航运贸易、海洋资源开发和海洋科学研究等活动，例如如远海石油开采，海上风机安装，海洋科学研究等日益增多。这些发展也导致了船舶大型化、多样化的趋势，同时越来越多不同的海上作业船只和海上作业平台也相继出现^[1]。例如在世界上第一个海上风电场，丹麦北极星风电场的建设过程中，便采用了巨型海上起重机对风电机组进行了整体吊装。执行该任务的海上起重机船需要实现在海洋某一点的精确定位或沿着预设的路线精确航行。诸如此类的对船舶操纵课题的出现，使得已有的船舶运动数学模型、模型参数辨识技术和船舶航向预报技术也亟需不断更新和进步，以满足现代船舶控制对于精度和可靠性的要求。

在工业领域信息化智能化脚步不断加快的趋势下，智能化船舶成为了世界上船舶制造和航运强国的追求目标。为了降低船舶管理和控制成本、减少人为因素对船舶运行可靠性和安全性的影响、提高船舶配套系统的运行效率、优化船舶航行线路等，从而在全球范围内开展了包括智能船舶在内的先进海上运输、开发系统体系的研究。其中DNV GL 公司在其发布的《未来航运业》一文中，提出了智能船舶的概念^[2]，是指具备实时数据传输汇集、高计算能力、数学建模能力、远程操控传感器和微型化的船舶。船舶智能化趋势对于船舶的操纵性能的要求使得船舶航向跟踪和船舶运动数学模型参数辨识的重要性再次得到了提高。

在船舶操纵系统方面，由于船舶尤其是远洋航行的大型船舶拥有很大的惯性，使得其运动具有非线性性。船舶在航行过程中由于其本身航速、载重的变化和在航行过程中海况的变化使得船舶模型的各项参数会发生变化 ^[3]。此外，诸如方向舵之类的控制装置与船舶动力学非线性耦合，这增加了船只控制的复杂性^[4]。在如今的航运智能化大背景下，船舶航向跟踪的意义就显得非常重要，船舶的航迹，航向，姿态等的监控和数据采集、分析对于船舶的控制和实现智能化起着至关重要的作用。而船舶模型和其辨识技术的改进、优化则是实现以上目标的基础。建立在不可靠的控制参数之上的控制器即便其理论先进、算法可靠，其对船舶运动的控制依旧是不可靠的。

1.2 国内外研究现状

1.2.1 船舶操纵发展现状

随着互联网、信息技术和人工智能的迅速发展，船舶操纵系统智能化已经成为了重要的研究方向，不同机构和公司也已经推出了许多计划甚至已经有了自动驾驶的商用货船投入使用。

在船舶操纵智能化领域，罗罗公司位于航运的智能化创新和发展的前沿，智能船舶的下一步发展是眼于远程遥控和无人驾驶。该公司在2014年就开始开发名为“未来操作体验概念”的岸基遥控系统^[5]，即将船舶驾驶室虚拟化，通过先进的传感设备，在岸上的控制中心内实现对船舶的远程控制。

据报道，罗罗公司已经实现了世界上第一艘遥控船的商业航行，罗罗公司未来的目标是从遥控商业海运轮开始到2035年实现自动无人的海运货轮^[6]。

日本和韩国也针对该技术趋势提出了各自的目标和计划。日本的“智能船舶应用平台项目”(SSAP)和韩国的智能船x.0计划。这两大计划通过其国内几大知名的船舶制造和航运业巨头的合作，来制定新的船舶发展方针，其中重要的目标都是从实现船舶和岸上控制中心的船舶操纵数据信息共享开始，逐步实现船舶操纵的智能化。

从国内来看，同时中船工业等已经提出了基于船舶智能化的发展方针。而《中国制造2025》中对智能船舶的发展指明了方向^[7]，其中重点是规划实施船舶领域的重要技术的研究，提高我国在与船舶相关技术领域的水平，从基础做起逐步实现船舶各个方面的自动化。

1.2.2 航向控制器的发展现状

目前，大多数商用船舶使用的的航向控制是以常规PID控制方法为主^[8]，该方法在实际船舶操纵领域的应用中体现出了结构简单易于设计的优点，但同时也暴露出该控制方法相关的参数的精度受设计人员经验影响较大的缺点，导致其在不同的航行条件下自我适应性能力不足，只能实现间断有限的调节^[9]。目前文献中常见的船舶航向非线性控制方法有滑模控制、自适应控制、现代鲁棒控制、反步法控制以及神经网络控制^[10]等，尽管这些算法拥有着很好的前景，但从现有的技术同时考虑经济效益来看，这些算法存在着需要的船舶运动数学模型复杂度过高，需要辨识的参数过多，同时存在不易得到的参数等的问题，因而在工程实际应用中未被广泛应用。

在实际应用研究领域，范云生等^[11]以大连海事大学“蓝信"号为研究对象，针对其航向跟踪控制的设计与实现进行研究在模型参数辨识基础上，设计一种模糊自适应PID航向控制器，并通过实验中常规PID控制器进行的对比证明了新方法的适用性。吴青等基于MPC控制方法设计了一种考虑各种约束和环境干扰的船舶轨迹跟踪控制器^[12]。Euan W. McGookin考虑到超大型船舶，尤其是超巴拿马级大型油轮航行运动控制中由于其巨大的惯性和低频特点而导致的响应滞后问题，提出了基于遗传算法的非线性船舶控制系统优化问题^[13]。它涉及到调节船只运动的两个系统的性能。这些系统通过滑动模式控制器以实现航向改变和跟踪保持。并使用遗传算法来优化滑模控制器的参数从而来优化整个系统在各种操作条件下的性能。S.Kumarawadu针对稳定而基于模型的水面船舶控制问题提出了船只自动操作方案。由于动态模拟的动力学模型具有强非线性和高度耦合的纵向（浪涌），横向（摆动）动力学和偏航动力学。对此提出了将横向和纵向控制合并为单个问题不简化动力学的控制方法^[14]。K.D.Do 和 J. Pan基于Lyapunov直接法和反推技术^[15]，利用船舶动力学的被动性及其相互关联的结构，开发了一种一种新的全局输出反馈控制器，用于跟踪控制欠驱动水面船舶，该控制器只需波浪冲击力和横摆力即可用，且无需对船舶速度进行测量。该方法可以通过将船舶运动的基础动力学方程映射为船舶速度相关的方程从而优化船舶的控制。

1.2.3 船舶运动数学模型研究发展现状

船舶运动模型识别从本质上来说是一类系统识别问题。系统识别是通过测量其输入和输出来了解系统数学模型结构的过程。船舶转向领域已广泛应用各种系统识别方法。船舶转向的动力学在评估机动性时很有用，而且在设计自动驾驶仪，导航和转向系统时是必要的。船舶的高度非线性行为是由向心和科里奥利加速度的影响，船体与其周围流体之间的相互作用以及波浪效应造成的。此外，诸如方向舵之类的控制装置与船舶动力学非线性耦合，这增加了识别问题的复杂性。

当前在船舶运动模型研究领域主要有两个方向，其一是基于基础的船舶运动和水动力之间的关系模型，通过求解水动力方程来确定船舶运动控制的参数。这种方法依赖的是数量很多的水动力系数的实验测量和对水动力导数的计算，在当前的技术条件下这些工作需要花费大量的时间和费用，同时船舶的控制系统对于不同参数的精度要求不同，而有些在船舶实际操控中要求较高的水动力导数通过一般的理论估计得出的精度并不能满足船舶控制的精度需要。于是便需要通过费用较高的实验手段去得出那些参数，而且存在可行性低的问题。其二是将将船舶看作一个动态响应系统，将舵角看作为系统输入，船舶在各个自由度上的运动看作是系统的输出。通过船舶的航行实验数据对该动态响应系统的传递函数和水动力参数进行辨识.该方法对于以开阔海域航行的大型船舶为代表的大惯性海上航行器等的系统有较好的适用性。

方法一的代表模型有以日本船舶学派为代表的船舶运动分离模型（MMG模型）和以欧美学派为代表的船舶运动整体模型。方法二使用的主要模型为响应型船舶运动模型（其代表为Nomoto模型）。

国外船舶对于船舶运动数学模型的研究从上世纪中旬便已开始，在几十年的发展过程中提出了很多富有建设性的模型和辨识方法。T.I.Fossen 等^[16]在船舶模型辨识中使用了卡尔曼滤波法进行递推辨识。此外在识别船舶动力学方面，Kallstrom和Astrom在上世纪八十年代对各种船舶采用了递归最大似然估计使得船舶数学模型识别精度得到了提高。之后Van Amerongen等人考虑当模型的输入是恒定时可使用间接模型参考自适应方法进行识别。Holzhuter率先应用了递归最小二乘估计方法对船舶模型进行了建立和辨识。而随着神经网络研究的的发展，其在船舶运动模型识别领域的应用也受到了重视。由于神经网络算法拥有的自我学习能力和对不同类型数据结构的适应能力，使其能在输入给它的大量数据中提取信息并进行学习，通过找到数据输入输出之间的关系^[17]。其中最常用的是包括BP神经网络在内的前馈型神经网络。针对该型神经网络存在的无法很好识别动态特性的缺点，孙洪波等^[18]将动态递归神经网络应用于船舶运动模型辨识中。本文所用的最小二乘支持向量机方法的原型支持向量机方法也逐渐被应用于计算船舶响应模型的流体力学导数中。

综上，我国在船舶航向控制、船舶运动数学模型研究乃至最近兴起的智能船舶革命领域起步较晚，与国外先进水平例如罗尔斯-罗伊斯公司已经初步实现商业化的遥控航运船只相比需要技术提升。在船舶航向预报、操作自动化等方面也还有一定的差距。未来的海运在可以预见的几十年间依然会是世界货运重要的组成部分，因此先进的控制技术和理念将会使得一个公司或者一个国家在海运和海洋资源开采上占得先机。我们在致力于追上世界先进水平的同时必须加强船舶领域基础课题比如船舶控制器设计、船舶运动数学模型辨识、船舶航向预报等领域的研究，一步一个脚印地推动船舶控制领域的发展。

第二章 船舶运动数学模型

2.1 船舶运动数学模型概述

船舶运动数学模型的建立是船舶设计、船舶控制和船舶实验仿真的重要组成部分。船舶建模大体上分为两个部分，船舶本体和外界干扰，外界干扰包括海浪，海风，海流，船舶本体包括舵角、螺旋桨、转向舵等。船舶运动的数学模型的准确与否，精度高低直接关系到对船舶航向的跟踪和控制的精度。

当前的主流船舶运动数学模型有以下三种：整体型结构模型、分离型结构模型（MMG）、响应模型^[19]。其中整体结构模型和分离型结构模型能在比较好地反映外界干扰的条件下描述船舶的多变量运动，这两种模型描述比较直接和完善的代价是其建模的复杂程度非常大，在这两种模型的建立中可能会包含难以识别的参数，导致过度识别或者识别错误^[20]。

例如MMG模型是一种通过对船舶在个自由度上的运动和所受到的外力进行分析，考虑水流，海浪等外力因素，通过水动力系数和船舶动力和控制设备之间的关系（例如螺旋桨与船舵的关系）对水动力进行建模。因而MMG方法需要测得的参数较多，由于船舶尤其是大型货运船只吨位、速度、吃水在内的参数在航行过程中会发生很大的变化，随之部分参数也会发生变化因而会导致建模的复杂性加大和低泛用性降低。

响应模型直接描述了船舶输入的舵角和输出的航向（首向角）之间的响应关系，同时该模型也在船舶控制系统的设计中被广泛采用。船舶响应模型的代表是Nomoto模型^[21]，Nomoto模型是由野本谦作提出的一种考虑船舶操作输出和舵角之间的响应关系的模型，并由此推导出了船舶舵角和船舶航向之间的线性方程来描述船舶运动。Nomoto模型由于它既能简单应用又能保持较好的精度而被广泛应用于航向预报中。在实际中与可以通过航行中采集的数据进行建模。

Nomoto模型是野本谦作基于二阶船舶响应模型进行优化得出的结果，他针对大型船舶的特点，认为大型船舶的动态响应特性在高频段由于船舶的巨大惯性显得没有价值，基于此将二阶的响应模型降阶为了一阶从而方便使用。Nomoto模型如下:

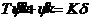（1）

Nomoto模型在针对小型、高速船舶的建模时，由于在这类种情况下一阶Nomoto模型忽略的高频段动态特性响应对船舶操纵控制的影响变大而使得仿真误差加大。同时由于忽略了海浪频谱中可能出现的低频段特性，使得Nomoto模型在面对高海况的恶劣条件下船舶运动仿真时存在着一定程度上的不足^[22]。尽管如此，该模型依旧由于其简单的结构设计、广泛的适用性和在船舶控制仿真中较高的精度，在船舶仿真、船舶控制器设计等领域成为了应用非常广泛的模型。

2.2 船舶响应模型的建立

在本文中，由于并没有船舶相关的水动力导数的数据，需要通过船舶实验测得的船舶的航向角的输出和舵角的输入的关系来建立和辨识船舶数学模型。因此选用船舶响应模型，同时鉴于实验船舶控制响应非线性的特点，将采用二阶非线性响应模型作为基础来建立船舶响应模型，并加上非线性项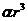使其符合船舶非线性运动的特点，该二阶非线性响应模型为：

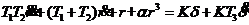(2)