海相软土桩的线性和非线性动力响应外文翻译资料
2021-12-25 16:41:27

英语原文共 11 页
海相软土桩的线性和非线性动力响应
摘要:本文给出了三根近岸钢管桩振动驱入海相软土系统在不同荷载水平下进行自由振动试验的结果。桩体按L型进行水平布置,桩头自由。该仪器由沿受载桩轴线的选定高度放置的应变计和位于受载桩头部的加速度计组成。本试验的目的是分析动力土-水-桩和桩-桩之间的相互作用,并研究在荷载水平增加时的非线性发展。给出了基于系统固有频率和阻尼比的试验模态分析结果,讨论了振动土-水-桩系统的复杂动力特性和桩与桩之间的相互作用。为了更好地评估线性行为范围内系统响应的可靠性,将应用荷载作用下的最低水平自由振动试验结果与冲击荷载试验结果进行了比较。
关键词:海相软土;土壤的非线性特性;桩基础;桩-土动态相互作用;现场试验;自由振动试验。
介绍
通常建立在单桩或群桩基础上的一类大型结构(如近海和近岸平台、风力涡轮机、码头、码头、系泊结构和桥墩)在侧向动力激励下的性能,在很大程度上取决于调节动力桩-土和桩-桩之间相互作用的复杂机制。在这些结构中,由于风、浪、船系泊、船的冲击力以及地震,可能会产生显著的动力效应,并可能导致早期损坏和破坏。
桩-土动力相互作用问题,特别是地震工程中,已经得到了许多学者的广泛研究,并发表了大量的理论研究成果。在试验领域,单桩和群桩的技术文献中,有一些关于室内试验和现场试验在静、循环侧向荷载作用下确定荷载-挠度p-y曲线的论文(Reese 等 1975;Matlock等,1980;布朗等。1987,1988)。相反,在现场条件下对全尺寸桩进行横向激励的动力试验(在近岸桩上的试验更少),文献报道较少。本文报道了超固结粘土(Blaney和Orsquo;Neill 1986)、软饱和泥炭(Crouse等, 1993)和硬粘土(M.Sa #39;don 等,2010) 的强迫振动和自由振动联合试验结果。研究表明,自由振动试验能够有效地表征土体的非线性行为。在饱和粉砂中也进行了强迫振动试验中(Jennings等,1985;Ting 1987),在较高荷载水平下,桩端附近出现局部液化,显著降低了桩身刚度。
由于缺乏实验证据桩-土动态交互的系统,尤其是在近岸条件,所以在意大利的拉斯佩齐亚米拉贝洛港进行了三根近岸钢管桩振动驱入到海相软土深度9.5米处的试验项目。对桩进行动力横向激励,即冲击试验和自由振动试验,目的是研究单桩和桩系在大、小应变下的动力特性。Dezi等(2012,2013)已经讨论了单桩和桩系的冲击荷载试验(极小应变试验)结果。
本文介绍了单桩和桩系的自由振动试验结果,目的是研究土-水-桩系统的动力相互作用,研究系统随着所加荷载增加的非线性动力行为。土-水-桩动力相互作用问题可以看作是一个经典的桩-土动力相互作用问题,其中海水在质量方面有一定贡献。通过试验模态分析确定土-水-桩系统的模态特性; 自然频率的值是从频率响应函数(FRF)的峰值估计的,而系统的阻尼比的平均值是用对数减量法研究自由振动来评估的。 通过自由振动试验获得的实验模态分析的结果,首先是关于单桩(土-水-桩系统),通过分析沿着桩中安装的应变仪的测量结果在浸入水中的部分和 在嵌入土壤中的部分中,然后通过分析放置在接收桩头部的加速度计的测量结果来确定桩系统(桩与桩的相互作用)。在这两种情况下,评估了土壤中产生的非线性对增加自由振动试验力水平的影响,并且通过比较自由振动试验的结果和Dezi等人提出的(2012,2013)冲击载荷试验获得的结果来分析系统的线性响应。
测试的地点和设置
在本节中,简要介绍了现场特征、试验场地和桩的检测方法。关于场地、岩土工程勘察和实验设置的更多细节可以在Dezi等人(2012, 2013)文章中找到。
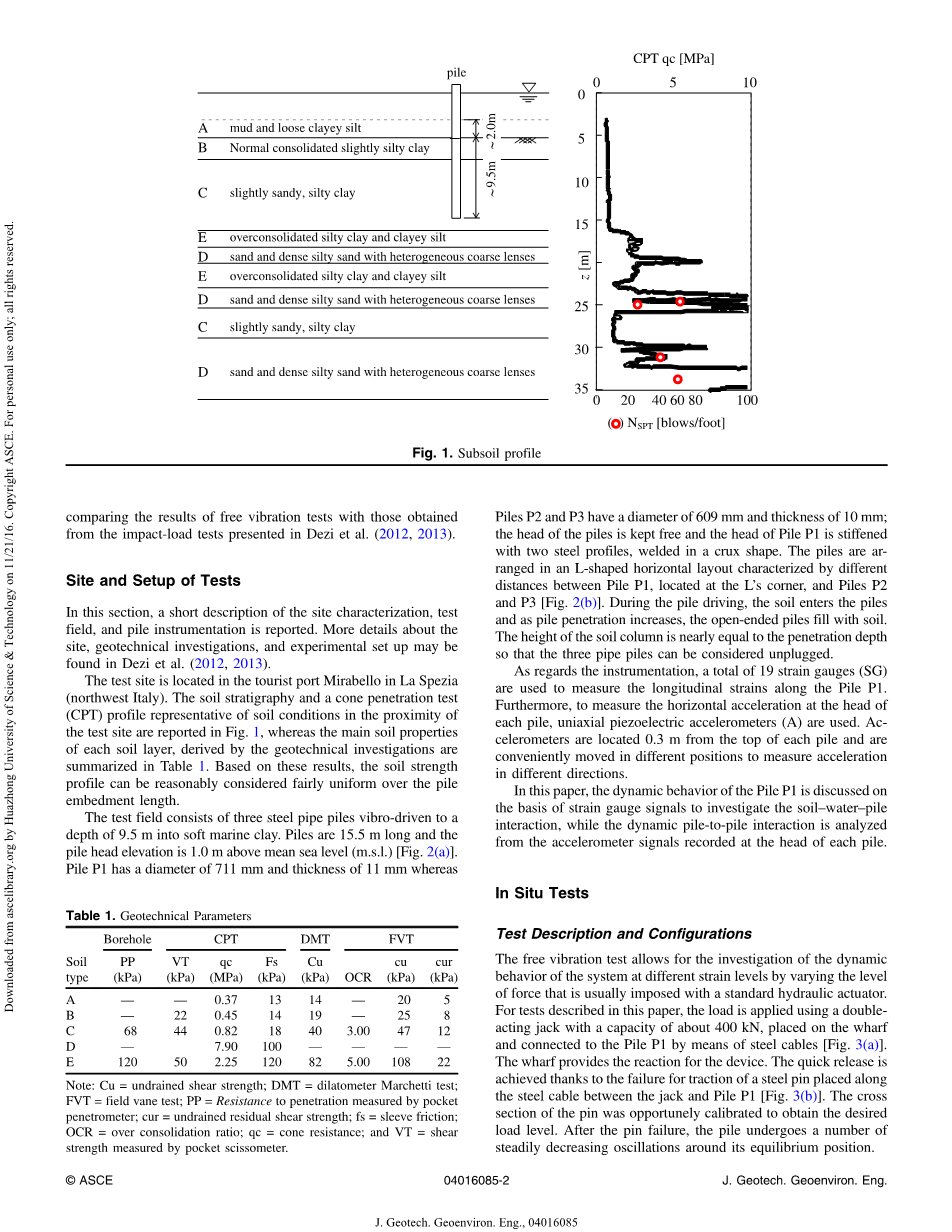
测试场地位于意大利西北部拉斯佩齐亚的旅游港口米拉贝洛。图1为代表试验场地附近土壤条件的土壤地层情况和圆锥贯入试验剖面图。而通过岩土工程勘察得到的各土层的主要土性如表1所示。根据这些结果,可以合理地考虑土体强度剖面在桩身埋设长度上的均匀性。
图1 下层土剖面
表1 岩土参数
注:Cu =不排水抗剪强度;DMT=Marchetti膨胀剂试验;FVT=现场十字板试验;PP=用小型贯入仪测量的贯入阻力;cur=不排水残余抗剪强度;fs=套管摩擦;OCR=超固结比;qc=椎体压入阻力;VT=用小型剪切仪测得剪切强度。
试验场地由三根振冲至9.5米深的软海相粘土中的钢管桩组成。桩长15.5 m,桩顶标高在平均海平面以上1.0 m (m.s.l.)[图2 (a)]。P1桩直径711mm,厚度11mm,P2、P3桩直径609 mm,厚度10mm;桩头保持自由,P1桩头采用两根钢型材加肋,焊接成十字形。桩体布置为L形水平布置,其特征是P1桩与P2桩、P3桩以不同距离位于L角[图2 (b) ]。在打桩过程中,土体进入桩内,随着桩身贯入量的增加,开口桩中填入土。土柱高度与渗透深度近似相等,可以认为三根管桩是不插拔的。
测量仪器采用19个应变仪(SG)测量P1桩的纵向应变。此外,采用单轴压电加速度计(A)测量桩端水平加速度。加速度计位于距每根桩顶0.3米的位置,方便地移动到不同位置,以测量不同方向的加速度。
原位测试
测试描述和配置
自由振动试验允许通过改变通常由标准液压执行机构施加的力的水平来研究系统在不同应变水平下的动态特性。在本文所述试验中,荷载采用双作用千斤顶施加,其承载力约为400kn,置于码头上,通过钢缆与P1桩连接[图3 (a)]。码头为装置提供反应。由于在千斤顶和P1桩之间的钢缆上放置的钢销[图3 (b)]牵引失效,故能实现了快速释放。销钉的横截面经过适当的校准,以获得所需的负载水平。销钉破坏后,桩体在其平衡位置附近经历了多次稳定减小的振动。
图2 (a)桩P1仪器;(b)试验场平面图;(c) P1桩平面图
图3 (a)自由振动试验试验场;(b)快速释放系统;(c)校正钢销
图4 自由振动试验装置
采用两种不同构型进行自由振动试验,P1桩(1)沿y方向释放,与P1桩和P3桩连接线对齐,(2)沿方向释放,与y方向呈45°角,分别称为和试验(图4)。沿x方向的测试没有进行,因为难以充分安排牵引系统。在每个测试过程中,沿y方向在每个桩顶处安装一个加速度计。时间采集4秒,包括2秒的预触发和5 kHz的采样率。对不同的负载幅值重复进行测试:使用不同的校准销在y方向进行5次测试,在xy方向进行4次测试。试验持续1天以上,先进行试验,后进行试验。
试验前,测量每根管桩内外的海水和土壤高度;在所有试验中,桩身以下约1 m处为海平面,桩身内外海床几乎处于同一水平,且在海平面以下约3.0 m处。因此,在不同的试验中,水、土高度对整个系统动力特性的影响可以认为是恒定的。此外,在试验前对主要由海浪引起的环境噪声进行了记录,得到0.0657 均方根(RMS)和低频含量(小于0.5 Hz),超出了研究范围。在实验测试中,环境噪声对应变和加速度值的影响可以忽略不计。
模拟压力传感器用于检测驱动千斤顶的泵的液压土压力。不幸的是,由于它的低灵敏度和冲压件与气缸壁之间的摩擦(受环境条件的放大),采用的测量系统受原始近似的影响。通过位于桩身上部的两个应变片(和)记录的值,可以更精确地估计千斤顶施加的实际荷载,在该位置,弯矩(因此纵向应变)随深度线性变化。实际应用荷载由下式得到:
(1)
其中E弹性模量;截面模量;;之间的距离。式(1)中的角可以由同一深度、、测得的应变得到,公式如下:
(2)
在表2中,报告了在每次试验中产生销钉牵引破坏(最大拟静力)和桩体快速释放的力值。由于牵引系统在对角方向设置高水平力时出现技术问题,在y方向进行了5级力的试验,在方向仅进行了4级力的试验。
表2 自由振动试验:实测和计算力
将低水平力下单桩和桩系的计算结果与Dezi等(2012,2013)的冲击荷载试验结果进行了比较。在自由振动试验前进行了冲击载荷试验。
单桩:实验结果与讨论
低水平力下的结果
在本节中,给出了土-水-桩体系在低水平力自由振动试验中的响应。讨论了沿桩身测得的应变,以及按频率和阻尼比计算的试验模态特性。
在图5中,记录了位于P1桩主母线(SG1、SG3、SG5、SG7、SG9、SG11)的6个应变仪在自由振动试验(Fy-1)过程中纵向应变的时间历程。与Dezi等人(2012)在冲击载荷试验中得到的结果进行了比较。自由振动试验的时程为原始信号,采用截止频率为100hz的巴特沃斯低通滤波器对冲击载荷试验的相关项进行滤波,几乎消除了要由高频成分引起截面变形和噪声的影响。 由于加载的准静态特性,与自由振动试验有关的时间历程在释放前几乎为常数。在快速释放后,桩的自由阻尼振动在土-水-桩体系的第一固有频率处表现出来(图6所示的FRF的较高峰值可以清楚地识别出来)。与Fxy测试相关的时间历史具有相同的特性,但为了简洁起见没有进行报告。值得注意的是,在这两个测试类型,即使压力的值是一半一个数量级不同,阻尼谐波振荡从定性的角度来看非常相似,和压力的最大值,与桩弯矩成比例,达到在同一桩部分位于下方的土壤表面(SG7)测试。
图5 SG信号的时间历程用于自由振动试验Fy-1
图6 SG信号的FRFs用于自由振动试验Fy-1
土-水-桩系统的模态特性,如固有频率和阻尼比, 可以通过试验模态分析,利用施加于桩顶的实测激励和应变仪沿桩身不同深度的系统响应,得到了自振频率和阻尼比来得到。[采用的方法在Dezi等人(2012)文中有更好的描述]。将激励和响应时程转换为频域来定义频响函数,即,响应测量值的傅里叶变换由输入的傅里叶变换归一化。采用峰值选取法,选取与FRF振幅峰值相对应的频率,得到固有频率。以Fy-1自由振动试验得到的SG5相关的频响如图6所示。只有一个定义第一固有频率的峰值是明显的,而与第二固有频率相关的峰值是不明显的,因为桩体从接近第一振型的变形形状中释放出来,因此优越的振型只受到轻微的激励。利用应变片信号在时域内的对数衰减量,估算了土-水-桩体系在低水平力作用下的阻尼比。应用该方法拟合前8个峰值,得到了系统在几乎整个桩体振动过程中阻尼的平均值。阻尼也可以通过拟合较低数量的峰来估计,例如前四个峰和/或后四个峰:为简便起见,这里没有报道,结果明显更分散,但平均值几乎与拟合八个峰得到的结果一致。
对主母线各应变片,考虑沿y方向(黑线)和xy方向(灰线)进行的自由振动试验和冲击载荷试验的测量值,得到第一固有频率和阻尼比,如图7所示。在冲击载荷试验中,频率和阻尼比的报告值是一组10次冲击的平均值。
通过比较两个方向和两种测试类型得到的结果,可以进行各种观察。在频率方面,自由振动和冲击荷载试验得到的第一固有频率沿桩身几乎是恒定的,这意味着这种动力特性实际上与SG沿桩身的位置无关。Fy-1试验在考虑所有应变片信号的情况下得到的平均值(7.47 Hz)与Hy试验得到的平均值(7.44 Hz)非常接近;这表明,在这两种情况下,即使自由振动试验引起的应变水平比冲击载荷试验引起的应变水平大得多,系统仍然具有弹性响应。另一方面,Fxy-1试验得到的第一固有频率均值(7.31 Hz)低于Fy-1试验,这可能是由于Fxy-1测试是在不同负载水平下进行的Fy系列测试之后进行的,并且在Fxy-1测试之前系统可能已经经历了线性行为。试验Fxy-1得到的频率平均值不仅低于Fy系列试验前Fy-1得到的频率平均值,而且低于Hy和Hxy (7.53 Hz)冲击载荷试验得到的频率平均值,证实了上述解释。
图7 首次自然频率和阻尼比评估从SGs沿桩自由振动和冲击载荷测试,沿y方向和xy方向
关于第一固有频率的平均值得到考虑应变仪信号的衔接和Hxy测试,细微差别可以主要归因于不完美的径向对称的系统由于U型钢型材焊接在管道保护应变仪和电缆。参照平均阻尼比率,平均值在所有从自由振动获得SGs测试非常接近一个负载测试获得的影响,为每个方向:7.2%和8.6%的自由振动测试Fy-1 Fxy-1和7.2%和7.8%的影响分别进行Hy和Hxy荷载试验。与每个SG信号相关的阻尼比值随着深度的增加而增大,特别是在Fxy-1试验中。阻尼本质上是由于能量辐射,通过应力波的传播,以及由桩和土的材料阻尼引起的耗散。P1桩头部释放的波首先沿着桩身向下传播,穿过水,然后又穿过泥土和海相粘土;桩周阻尼的不同主要是由于材料不同,阻尼特性不同。特别是考虑到管桩的材料阻尼一般较小,前面所述的沿管桩的阻尼趋势可以解释为,在更大的深度(对应的SG8,SG9和SG10),较多的土体参与了能量耗散,即辐射和土体阻尼。
最后,与冲击载荷试验Hy和Hxy相关的阻尼比值基本相同,与试验Fy-1所得阻尼比值相近。
高水平力下的结果
为研究高应变水平土-水桩体系的动力特性,研究土体非线性对桩身动力特性的影响,进行了4种高荷载水平下的自由振动试验;最大力(58.1 kN)约为表2所示最小力(2.8 kN)的20倍。在本节中,我们讨论了应变(实测值和频响)和系统动态特性(频率和阻尼比)方面的结果。
图8 沿桩身不同荷载水平沿y方向和xy方向的应变和弯矩,在快速释放前测得
图8为SGs在最大准静态荷载作用下,在快速释放前沿桩身测量的应变(以及与应变成比例的弯矩)。对于每个荷载水平,实验数据(用点表示)采用四阶多项式函数(连续
资料编号:[3732]




