钢箍筋和/或FRP夹套约束混凝土的应力-应变分析关系外文翻译资料
2022-08-05 14:55:37

英语原文共 15 页,剩余内容已隐藏,支付完成后下载完整资料
钢箍筋和/或FRP夹套约束混凝土的应力-应变分析关系
佛朗哥·布拉加、罗萨里奥·吉利奥蒂和米开朗基罗·拉特扎
摘要:本文基于弹性力学理论,建立了钢筋混凝土构件核心部位横向钢筋围压的平面应变分析模型。首先对带有方形和圆形箍筋的加固截面进行围压分析评估,然后对带有方形和矩形箍筋以及辅助横拉杆的更复杂的加固配置进行分析评估。最后,利用该模型对纤维增强聚合物FRP、S-玻璃、钢等材料的外包装围压进行了评价,并设计了更好的围压技术和围压材料组合。为了得到被动约束下的应力-应变曲线,引入了方形截面和圆形截面的类比。这样,就可以使用由圆柱形试件三轴试验得出的任何主动约束模型。通过与现有模型和试验结果的比较,验证了该模型的正确性。
内政部:10.1061/ASCE0733-94452006132:91402
CE数据库主题:应力应变关系;混凝土;纤维增强聚合物;弹性。
介绍
钢筋混凝土结构的分析需要对所有组成材料进行正确的建模。钢和混凝土的性能对结构及其构件的刚度、强度和延性有很大的影响。此外,混凝土的应力-应变关系既取决于材料的特性,也取决于其与横向和纵向钢筋的相互作用。
根据约束问题的典型方法,方形或矩形截面混凝土核心上箍筋施加的侧向力应集中在边缘,并通过拱作用分布在截面内。因此,箍筋的抗弯刚度被忽略,箍筋的侧面被认为是角部之间的连接。然而,这些假设并不总是合理的,尤其是当拉杆直径与其长度之比增大时。
作用在边缘之间的力是通过使用“自由体图”的简单平衡获得的,因为横向钢筋中的应力应等于屈服应力
实际上,对于混凝土中的低应变水平,横向钢筋中的应力状态非常小,混凝土基本上不受约束。相反,当混凝土中的应力接近其单轴抗压强度时,会出现渐进性内部开裂,横向应变显著增加。因此,作为“被动约束”的横向钢筋提供了一致的约束响应
被动约束与围压分析评价
受纵向压缩应变影响的钢筋混凝土柱倾向于横向扩展。横向钢筋,如钢箍筋、内部系杆和/或纤维增强聚合物FRP夹套,会产生限制作用,从而阻止混凝土芯的膨胀,从而导致构件内部出现三轴应力状态。
钢筋混凝土构件梁和柱的几何形状,其纵向尺寸相对于横截面尺寸是主要的,允许我们研究涉及一般代表性横截面的问题。
平面应变条件下的被动约束
该模型的关键假设是混凝土截面的应力增量不产生任何平面外应变。这意味着横向钢筋的约束应在Laterza 1996;Braga和Laterza 1998的平面应变条件下进行。
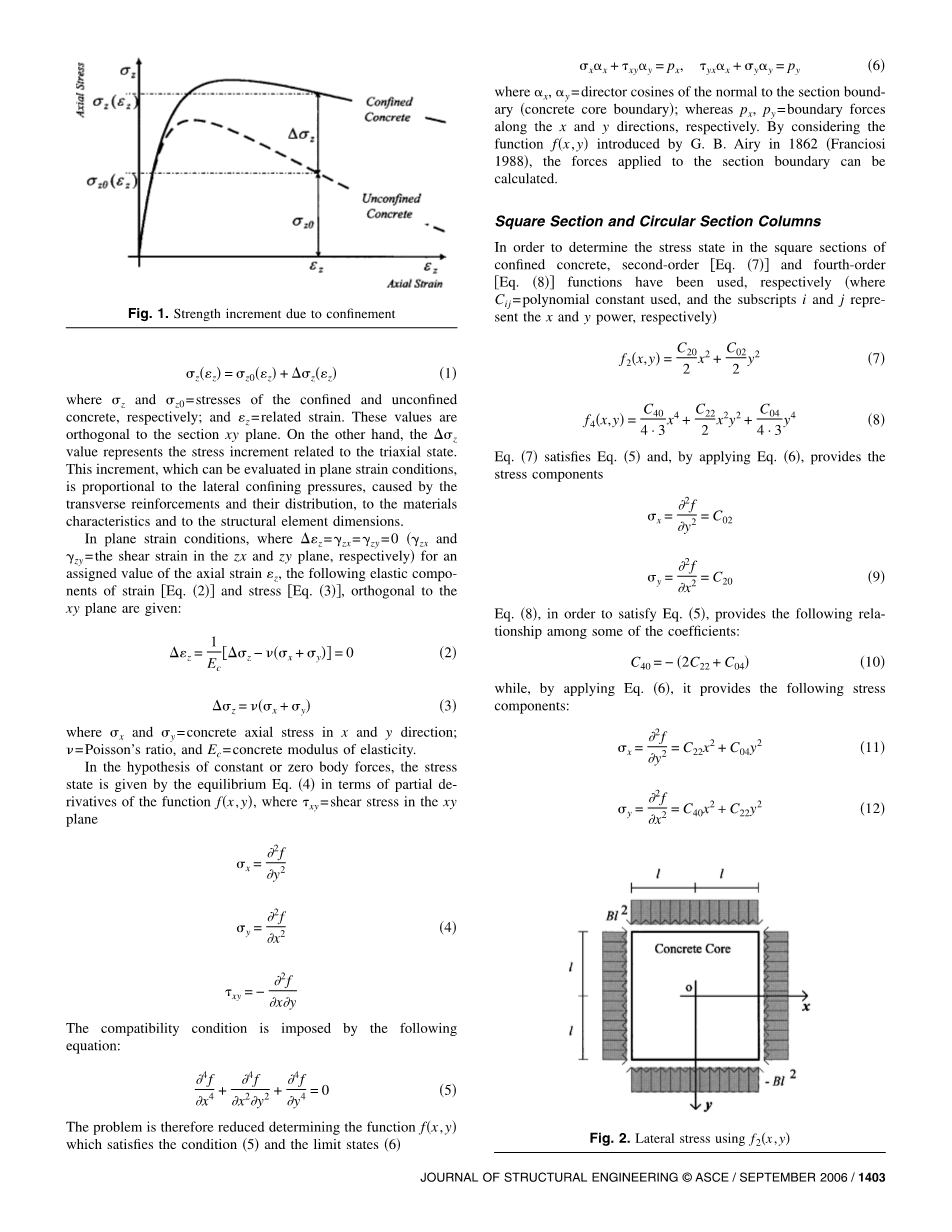
表征混凝土性能的应力-应变关系如图1所示。一般来说,这种关系可以写为:
图1。约束引起的强度增量
zz=z0z zz 1
式中,z和z0分别为约束混凝土和无约束混凝土的应力;z为相关应变。这些值与截面xy平面正交。另一方面,z值表示与三轴状态相关的应力增量。这种增量可以在平面应变条件下进行评估,它与横向钢筋及其分布引起的侧向围压与材料成比例
特征和结构元件尺寸。
在平面应变条件下,其中z=zx=zy=0 zx和zy=zx和zy平面中的剪切应变,对于轴向应变z的赋值,给出了与xy平面正交的应变式2和应力式3的以下弹性分量:
1
|
z=zminus;x y=0 Ec |
2 |
|
z=x y |
3 |
式中,x和y=x和y方向上的混凝土轴向应力;=泊松比,Ec=混凝土弹性模量。
在恒定或零物体力的假设中,应力状态由平衡方程式4给出,表示函数fx,y的偏导数,其中xy=xy平面上的剪应力
4 x22 y4=0.5y
十
因此,通过确定满足条件5和极限状态6的函数fx,y,问题就简化了
xx xyy= px, yxx yy= py6 其中x,y=垂直于截面边界混凝土核心边界的方向余弦;而px,py=分别沿x和y方向的边界力。通过考虑函数fx,y 由G.B.Airy于1862年引入,franciosi1988,可以计算作用在截面边界上的力。
方形截面柱和圆形截面柱
为了确定约束混凝土方形截面中的应力状态,分别使用了二阶方程7和四阶方程8函数,其中Cij=多项式常数,下标i和j分别表示x和y的幂
C
f2x,y = 20x2 C02y2 7
f4x,y = C40 x4 C22x2y2 C04 y4 8
4 · 3 2 4 · 3
公式7满足公式5,并通过应用公式6提供应力分量
2f
x=y2 = C02
2f
y=x2 = C20
9
为了满足式5,式8提供了一些系数之间的以下关系:
C40 = minus; 2C22 C04 10
同时,通过应用公式6,它提供了以下应力分量:
|
2f x=2 = C222 C042xy y |
11 |
|
2f y=2 = C402 C222xy |
12 |
十
|
图3。横向应力f4x,y
|
|
xy= minus;= minus; 2C22xy xy 通过假设,因为几何对称 |
13 |
|
C20 =C02=minus;Bl2 此后,导出所报告的表达式15 2f2 x=2 = minus; Bl y |
14 |
|
2f y=2 = minus; Bl2 |
15 |
2
十
2f
xy== 0
xy
这表示图2沿边界的恒定压缩,其中B=恒定,l=横向半长。
考虑多项式8并假设C40=C04,条件C40=C04=minus;C22得到。
如果假定压力等于A,则
C40=C04=minus;A,C22=A,可获得表示沿边界线抛物线变化的牵引力和线性变化的切向应力的应力表达式16,如图3所示
将式16与式15相加,即。获得17个。它们指的是抛物线变化的法向应力和线性变化的切向应力,如图4所示。
x= Axminus; y minus; Bl, = Ayminus; x minus; Bl, = minus; 2A xy2 22y2 22xy
17
|
图4。侧向围压f2x,y和f4x,y之和
|
通过改变A和B的值,混凝土和约束钢筋之间的力可以在形状和强度上发生变化。可以观察到这样一个力系,通过使用Airy函数fx,y,确保了平面应变条件。当压应力为正时,我们得到
z=x y=minus;Ax2minus;y2minus;Bl2 Ay2minus;x2minus;Bl2=2Bl2
18
因此,强度增量在截面的每个点都是恒定的。
可以注意到,当考虑混凝土上箍筋侧向压力的估计分布时,需要钢-混凝土界面处不同于零的切向应力值,以满足平面应变的平衡条件。这些切向应力最初是由于箍筋和混凝土之间的粘结造成的,然后,当混凝土大量开裂时,粘结条件的恶化通过混凝土芯膨胀产生的摩擦力的增加来平衡。
就圆形或螺旋形截面而言,艾里的
函数提供关系19,用极坐标表示,对应于钢筋施加在混凝土芯上的均匀径向压力fr
q
fr= n = m = 19
S
式中,n=径向;m=与n正交的边界相切的方向;S指环向或螺旋间距。
因此,对于圆形或螺旋箍筋约束截面,可得出以下轴向应力增量方程:
问
|
z=n m=2n=2 S 混凝土与约束钢筋的相互作用 在平面应变条件下,应变分量为 |
20 |
||||
Ec |
21 |
||||
Ec |
22 |
Ec
对于x和y方向上的混凝土芯位移Vx和Vy,以下关系成立:
Vx=xx 21xyy, Vy=yy 21yxx23
通过使用图4中的对称性问题(它允许我们只考虑截面的四分之一),并通过选择两个主方向y中的一个,获得截面平面内的应变和位移的以下表达式
特别是,当y=minus;l时,等式26产生了与横向拉杆正交的x方向上混凝土芯边界的变形形状。此外,将等式26除以l,当y=minus;l和x=l时,得到平行于横向拉杆的平均应变c-平均值
对于圆形截面,混凝土径向n
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[261718],资料为PDF文档或Word文档,PDF文档可免费转换为Word




