框架结构的应力-合成塑性外文翻译资料
2021-12-13 22:18:32

英语原文共 11 页
框架结构的应力-合成塑性
美国土木工程师协会准成员Sherif El Tawil和美国土木工程师协会成员Gregory G.Deierlein著
摘要:在应力-合成空间中有两种形式的边界面塑性模型,其适用于钢及钢筋混凝土结构的分析,以及对组合梁柱的分析。第一种模型是适用于有限弹性区域钢构件的双表面模型。第二种是为钢筋混凝土和钢-混凝土组合构件而开发的,采用了一个无限小的荷载面退化到某一点的单外边界面。本文回顾了这些模型在建立过程中所采用的基于塑性的假设,并根据梁柱截面的基本数据的分析,对预测的塑性流动方向进行了评估,并对约束面公式提出了改进意见,同时评估的结果有力的支持了应力合成空间中使用的Mroz运动学规则。
梁柱的应力合成塑性模型充分考虑了经典应力空间的塑性准则在轴力和弯矩联合作用下的非弹性截面变形模型的适应性。在此条件下,塑性模型是通过对横截面上的离散点的行为进行监测,而非弹性效应则是使用基本的应力应变关系进行明确的建模。本文讨论了与轴向推力和双轴弯矩相关的截面应力的三维梁柱的塑性公式。本文所提出的塑性模型将这些力与广义截面应变(如轴向应变和曲率)在单调和循环荷载下联系起来。在局部失稳效应(如局部屈曲)不起关键作用的结构中,应力合成塑性模型对于大型建筑框架的分析是准确和有效的。用于框架结构应力-合成塑性模型公式的分析已经发展了大约30年。Nigam(1970年)、Porter和鲍威尔(1971),Orbison等人(1982),Hilmy和Abel(1985),Powell和Chen(1986),赵(1993)曾进行过与本次论文有关的实验工作。应力-合成塑性模型也被应用于钢筋混凝土构件和钢管混凝土。
钢构件最基本的应力合成塑性模型为塑料铰链型,当满足规定的屈服准则时,其杆端假定为突然从弹性变为完全塑性。屈服准则函数通常采用连续或分段线性的形式,用来表示构件在轴向载荷和弯曲作用下构件的完全屈服强度。这类模型分析时一般采用相关的流动规则,其中塑性变形(轴向伸长率和旋转)受约束作用通常发生在与屈服表面垂直的方向上。近来,有关学者提出了使用两个或多个嵌套屈服表面考虑渐进式构件屈服时的精化模型。
应力合成边界面模型适用于钢构件,它由一个内力(或加载面)组成,它代表截面的初始屈服准则和一个表示完全塑化状态的外部(或边界)表面。模型的加载面受约束在边界面内移动,为了计算方便,通常假定加载面是边界面的简化。当构件承受的力位于加载面内时,截面为完全弹性截面。当力点接触到加载面时,假定屈服开始。 在塑性加载过程中,力点保持在内载荷面上,两个表面的运动受运动规律的控制。这种模型最初是Hilmy和Abel(1985年)用来对钢结构进行地震分析,后来被其他人用于模拟钢连接(赵1993)和钢管混凝土构件(Hajjar等人)。(1997年)。
图1 P-Mz空间中的边界曲面模型
本文遵循了与前面所提到的的模型类似的研究路线,但有一个重要的区别,这与非弹性变形的建模有关。所有前述模型均为集中塑性或塑性铰型,其中构件末端力与构件端部变形有关。因此,在这些公式中使用的塑性关系需要通过关于塑性铰链长度、轴向载荷水平和弯矩的假设,对整体构件的响应进行校准。本文讨论的是另一种形式,即在横截面上应用边界面模型,将应力结果与广义截面应变联系起来,即,相对于截面质心而测量的轴向应变和曲率。正因为如此,我们对边界面模型的评价可以局限于考虑构件的横截面行为。
基于应力合成塑性的公式,特别是适用于钢构件的公式的一个一般特点是存在一个有限载荷面来表示弹性响应区域,如[图1-(a)]。钢筋混凝土和混凝土组合构件通常具有较小的初始弹性区域,而会在循环荷载作用下消失。为了模拟这类构件的行为,[El-Tawil和Deierlein 1996(b)]开发了边界面模型的一个版本,将加载面退化到一个点[图1(b)]。正如达菲和波波夫(1977年)所指出的, 加载面的这种退化带来了一个问题,这与塑性公式一般假定存在有限的加载面来建立控制塑性的规则相悖。但是,可以通过考虑加载表面尺寸接近于零的极限情况和使用运动规则推断位置来克服这一困难。边界面上的这一点表示无限小加载面上的共轭点,用来控制塑性流动方向。与有限尺寸加载曲面不同的是,无限小载荷面共轭点的确定取决于运动硬化准则的选择。
尽管应力合成塑性得到了广泛的应用,但几乎没有做什么工作来验证从经典应力空间塑性理论中所采用的基本假设是否适用于部分塑化截面的应力合成空间。对于完全塑化的截面,可以证明塑料流动必须在完全塑化的边界面法向方向流动。这证明了在基于弹性-完全塑性铰概念的公式中使用相关的流动规则是正确的。但是却没有类似的理论依据来确定构件部分被塑化时的塑性流动方向,并且支持加载面是按比例缩小的边界曲面假定依据。此外,对于加载面退化到某一点的模型,尚不清楚在可用的运动学规则中哪一个可导致边界面上出现最合适的共轭点。
本文以数值纤维型截面分析为基础,研究塑性流动的方向,并与应力合成塑性假设进行比较。分析钢、钢筋混凝土和复合钢混凝土截面在轴向荷载和双向弯曲作用下的作用。纤维类型分析仅受平面截面剩余平面假设和理想单轴材料应力应变模型的限制。应力合成模型包括计算外边界面和内屈服面,利用塑性准则确定力与广义应变之间的关系,即,关于塑性流动方向和将应变分解为弹性和塑性部件的假设。本文讨论的关键问题是应力合成塑性理论所假定的塑性流动方向是否与由纤维截面分析得到的基本数据所确定的方向一致。
横截面纤维分析
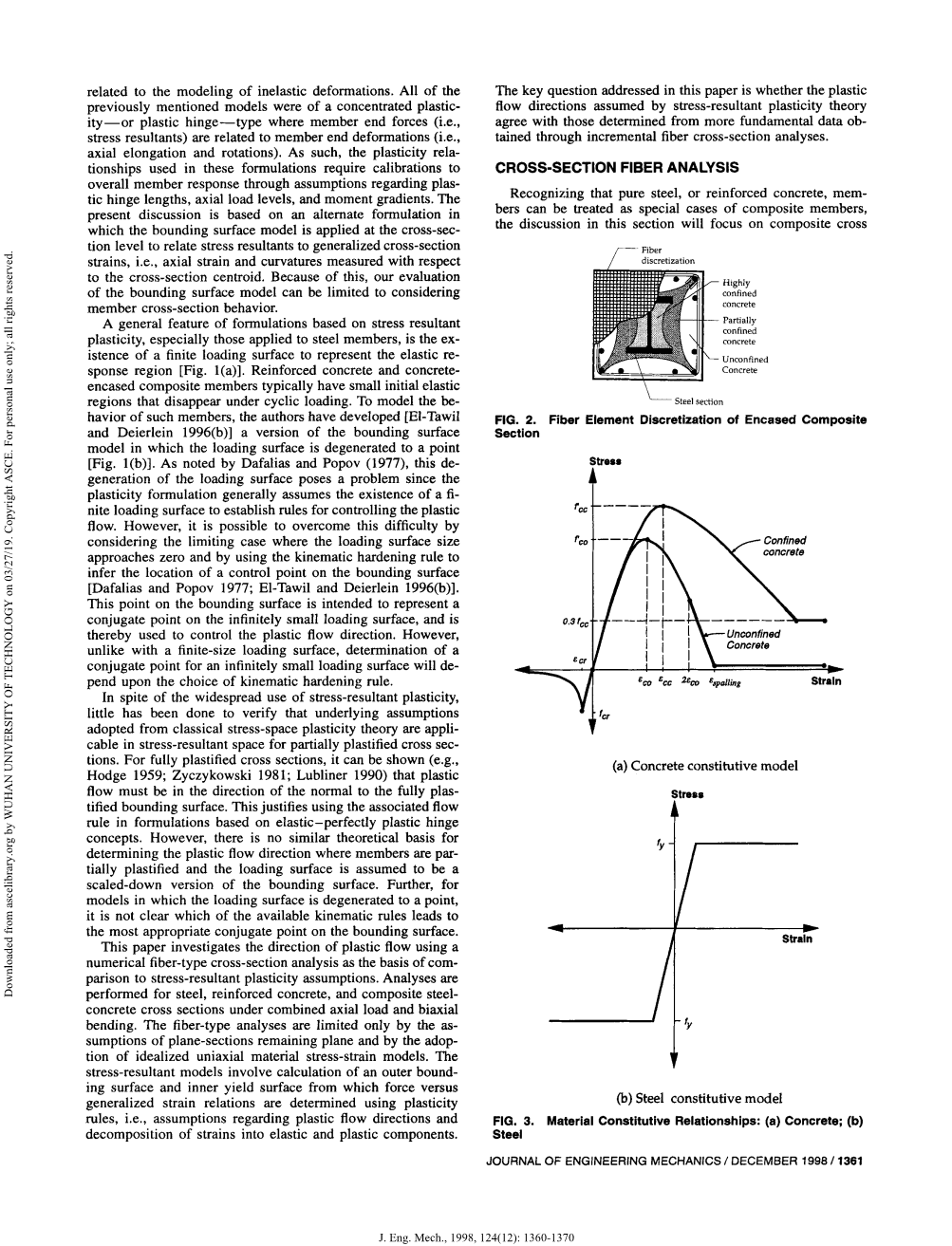
图2封闭复合材料截面的纤维单元离散化
(a)混凝土结构模型
(b)钢结构模型
认识到纯钢或钢筋混凝土构件可视为复合构件的特殊情况,本节的讨论将集中于复合截面。包覆构件的纤维单元分析要求将截面离散为多个小区域(纤维),其构件模型的建立基于单轴应力与应变的关系。每个区域代表沿着构件纵向运动的一根纤维,可以被指定为几个本构模型中的一个,代表不同约束量的混凝土[图3(A)],结构钢[图3(B)],或是钢筋。通过标准迭代程序得到截面对外加荷载(轴向力和弯矩)的响应。假设平面截面保持平面,从而意味着钢构件与周围混凝土之间产生完美结合,混凝土中的剪切相互作用和徐变/收缩效应没有得到考虑,钢筋或结构钢截面的局部屈曲也没有考虑在内。
应力合成塑性
用表示应力结果,然后将相应的广义应变e定义为
其中,表示与广义应变变化相对应的内部功的变化。Omega;表示计算积分的域。对于横截面分析,Omega;等于梁柱构件的单位长度,(1)简化为
如图4所示,表示轴向和弯曲力。
其中P为施加的轴向载荷;为施加的大弯矩和小弯矩。向量e表示截面应变。
其中ε表示横截面质心处的轴向应变测量,分别是关于大弯曲轴和小弯曲轴的曲率。
形式的函数用应力结果描述加载(或初始屈服)表面。当力点位于该表面时,假定发生塑性加载。这里,塑性耗散被定义为
其中ep是广义应变矢量e的塑性分量。Drucker(1951)认为加工硬化(或稳定)塑性材料在增量加载过程中所做的功是正的,而在加载-卸载循环中所做的功是非负的(零或正)。这一定义通常被称为德鲁克假设,此假设可推广到截面的应力合成分析。加工硬化(或稳定)截面在增量加载过程中所做的功[见(1))]是正的,而在加载-卸载周期中所做的功是非负的。对于德鲁克意义上稳定的加工硬化段,最大塑性耗散原理可以写为
结合公式(5)可得
图4力的定义,截面应变
对于任何,使得f():是位于加载表面或其内部的一个力点。公式7导致经典塑性理论中的两个重要结论:加载表面的凸性,以及相关流动的正态性条件。换句话说,如果截面的弯矩-曲率和轴向载荷-轴向应变曲线总是硬化,则在Drucker(1951)假设意义上是稳定的,则由轴向载荷-弯矩的凸性可以推断出正常表面的塑性流动和表面的塑性流动。塑性规则应用于实际情况的主要困难是:(1)合适的加载面确定;(2)描述塑性加载过程中表面在应力合成空间中的变形和移动。
边界曲面模型
为了建立一种适用于钢、钢筋混凝土和组合梁-柱混合结构分析的模型,作者提出了两种基本界限的变化形式。模型称为有限载荷面(FLS)和简并加载面(DLS)。由于篇幅有限,本讨论仅限于描述与塑性假设有关的模型的概念方面;完整的公式在其他地方提出。如图所示[图1(a和b)],FLS模型适用钢截面、DLS模型适用于钢筋混凝土和外边界截面。
本节介绍的边界面模型提出了截面的塑性刚度特性,即塑性广义应变与应力结果之间的关系。在相关研究中,作者利用这些关系建立并实现了非弹性单元刚度矩阵,建立了梁柱塑性扩展效应的模型。简单地说,单元刚度公式涉及以下步骤,即从边界上确定出横截面应力与塑性应变之间的关系。
RFACE模型:
1.对截面力-应变关系进行了区分,得到了将增量力与广义应变联系起来的截面切线柔度矩阵。
2.然后沿构件长度对横截面切线柔度项进行数值积分,以确定构件柔度矩阵。
3.然后将该矩阵进行倒置和扩展,给出构件的刚度矩阵,然后将其合并到一个标准的非线性框架分析程序中。
因此,利用这种方法,边界面模型考虑了构件截面的塑性扩展,以及非弹性截面特性的数值积分、塑性沿构件长度的扩展。
有限载荷面(FLS)模型
虽然本文的讨论适用于三维力空间(P,My,Mz),但对于图中的载荷面和边界面是适用的。为简单起见,在二维中显示为图l(a)。外边界面被校准以匹配该构件的完全塑化强度,而内部表面只是该边界表面的一个简化版本。这种内表面形状的选择是为了方便,不一定符合真正的初始屈服准则的截面。如下文所示,这对计算塑性流动有影响。当表示作用在横截面上的力点进入时,就会检测到塑性载荷。当与内加载面接触时,在连续的塑性载荷下,载荷和边界面根据Mroz(1967)运动硬化规则导出的方程在力空间中转换。
图中的图表1(a)对应于一种情况,即在先前的塑性加载和卸载之后,截面处于力点A处重新加载的边缘,从而导致加载。当截面加载时,共轭点Alsquo;位于边界面上,使得Arsquo;与加载面上的点A具有相同的单位法线g。根据Mroz的运动规律和一致性条件,在塑性加载过程中,两面沿线D平移,即将力点与共轭点相连接。坏处稳态条件下,内载荷面的运动速度要求力点停留在加载面上。
简并加载面模型(DLS)
加载表面的存在是建立上述类型塑性模型的关键,因为加载、卸载和塑性的定义都是如此。流动方向取决于加载面。当加载面不存在时,例如没有有限弹性区域的单元,在多维载荷下就会出现问题。当加载/卸载准则和塑性流动方向明确定义时,单向加载就不会不存在此类问题。
正如Dafalias和Popov在对应力空间塑性的处理所提出的,克服这一条件的一种方法是假定加载表面确实存在,但在极限处中退化到某一点。然后,有限边界面作为加载面,定义塑性流动规则。这种方法需要在边界表面确定一个合适的共轭点,以正确地表示当前力点的塑性行为和加载/卸载条件。这个共轭点的位置取决于所使用的运动规律。通过由Dafalias和Popov提出的应力空间公式,我们研究了以下五种运动规律,以确定在边界表面上形成一个逻辑共轭点:Prager(1956);Ziegler(1959);Mroz(1967);Phillips和Weng(1975);Tep and Lee(1983)。其中,我们发现Mroz的规则产生了最一致的结果,并且是最容易实现的。如上文所述,FLS模型是Mroz模型的一个基本特性其规律是屈服面的运动沿连接加载面上的力点到边界上的共轭点的线进行。对于DLS模型,假设
- 加载点沿力增量方向运动
- 加载点与加载面运动一致
- 表面运动方向与加载点与共轭点的矢量平行(Mroz法则),运动与加载点与共轭点的矢量平行(Mroz法则),共轭点作为力增量向量延伸的交点。
流动规律的数值检验
如前所述,FLS模型的内载荷面被假定为尺寸固定且在空间上平移的边界面的简化版本。然而,人们认识到对于梁柱截面,真实的初始屈服面与全塑面不同,在塑性加载时,表面变形是非唯一的。因此,塑性模型中固有的假设是一种不准确的假设,可能无法准确地反映真实的行为。为了评估这些假设,考虑了几种单调加载情况,其中将假定的加载面和正态条件所隐含的塑性流动方向与塑性进行了比较。DLS模型出现了共轭点如何位于边界表面有关的问题。
尽管纤维分析可以模拟钢筋混凝土和复合截面处的力与广义应变行为(如弯矩曲率)的峰值后的下降响应。但在塑性流动数值研究中,只有Drucker意义上稳定的正载荷区才能用于塑性流动的数值研究。这并不一定意味着在横截面上不可能有个别纤维的软化(例如,由于混凝土开裂),但它确实要求整体的横截面行为。或者不能经历应变软化。
如下文所述,塑性流动方向根据塑性变形矢量与横截面主轴之间的角度,用“流动角”来描述。流量数据从纤维分析中得到的a称为数值角度,而假定塑性理论中隐含的数值称为APT角。
流动角计算
由纤维分析得到的塑性流动角首先由给定载荷下的轴向应变和截面曲率定义的总广义应变来确定(见图4)。为了简单起见,“广义”一词将被删除,而广义的应变将被称为“纯应变”。对于相同的载荷,弹性应变由简单关系和计算,假定具有完全弹性的无裂纹横截面。然后,将塑性应变计算
资料编号:[5443]




