基于模型学习的自适应遗传算子研究毕业论文
2020-04-08 13:19:22
摘 要
遗传重组算子是多目标进化算法中的一个重要组成部分之一。目前广泛采用的模拟二进制交叉算子通常采用固定参数,搜索效率低下,不能很好的适应日趋复杂的多目标优化问题。本文针对模拟二进制交叉算子的不足,提出了一种基于模型学习的自适应遗传算子——MLSA-SBX。该算子首先使用局部主成分分析将繁殖池划分为几个不相交的簇,再对每个簇分别判断进化情况,使用自适应策略,并仅在每个簇内进行杂交。我们在具有决策变量耦合关系的多目标优化问题RM-MEDA测试集上利用NSGA-II算法进行测试,对两种算子进行了分析比较,所得结果表明虽然MLSA-SBX的计算复杂度较大,但在处理具有耦合关系的问题时使用MLSA-SBX比使用SBX能明显提升算法的性能。
关键词:;遗传重组算子;自适应;模拟二进制交叉;多目标优化
Abstract
Recombination operator is an important part in multi-objective evolutionary algorithms. Now the widely used simulated binary crossover usually keep fixed parameters throughout a simulation run, which seems to be inefficient and can’t adapt to complex multi-objective optimization problem well. In this paper, considering the disadvantage of simulated binary crossover, we proposed an model learning based self-adaptive genetic operator—MLSA-SBX. First, we use local principal component analysis to participate the mating pool into several disjoint clusters, then judge the population evolved in which level. Individual will only cross with the in the individual in the same cluster using an adaptive strategy. We use NSGA-II to test these two operators on a set of multi-objective optimization problem with variable linkage (RM-MEDA test set). Experiments have shown that, although MLSA-SBX has a high computation complexity, it outperforms SBX on multi-objective optimization problem with variable linkage.
Key Words:genetic combination operator;self-adaptive;simulated binary crossover;multi-objective optimization problem
目 录
第1章 绪论 1
1.1 研究背景与研究意义 1
1.2 国内外研究现状 3
1.3 本文主要工作与组织结构 7
第2章 相关理论基础 9
2.1 非支配排序进化算法 9
2.1.1 快速非支配排序 9
2.1.2 拥挤度排序 10
2.2 模拟二进制交叉算子 11
2.3 局部主成分分析 14
第3章 基于模型学习的自适应遗传算子 15
3.1 SA-SBX 15
3.2 MLSA-SBX 16
第4章 实验结果 18
4.1 测试问题 18
4.2 IGD指标 21
4.3 实验参数设置 21
4.4 实验结果分析 22
第5章 总结与展望 32
5.1全文总结 32
5.2未来的研究思路 32
参考文献 33
致 谢 36
第1章 绪论
1.1 研究背景与研究意义
现实生活中,经常会遇到需要同时优化两个或两个目标以上的问题,例如在购买车时,买家既追求汽车的舒适性,又希望价格越低越好,还期待汽车的耗油少,我们称这类问题为多目标优化问题(Multi-objective Optimization Problems,简称MOPs)。MOPs广泛地存在于物流调度、资源分配、数据挖掘、生物信息、图像处理、模式分类等领域,因此引起了广大研究人员的兴趣[1]。MOPs的数学表达形式如下:
其中表示决策空间,称为决策向量(Decision vector)(D表示决策向量的维度),上面例子中的舒适性、价格和耗油量就组成了一个三维的决策向量。由m个目标函数()组成,则目标空间为。与单目标优化问题(Scalar-objective optimization problems,简称SOPs)不同,MOPs中的目标往往互相排斥,因此几乎不存在一个能够使得这些目标同时达到最优的解。除非决策者(Decision maker,简称DM)对每个目标都有一个偏好权重,这时我们就可以将MOP问题转化为一个SOP再进行求解即可。然而在很多情况下,我们并不能提前获知DM的偏好亦或说DM不能提前决定他们的偏好,那么也就无法采取这种方式进行求解。但我们可以找到一组最优均衡解(trade-off solution),称为帕累托最优解(Pareto optimal solution),这组解相互之间不存在绝对最优。找到这组解后再将其交给DM,由DM来决定选择哪一个或哪几个解作为最终的最优化方案。帕累托最优的相关概念定义如下[1]:
定义1. 帕累托支配(Pareto Dominance):设向量,向量,若对于,都有,且,使得,则称向量(帕累托)支配向量,记作。
定义 2. 帕累托集合(Pareto Set,简称PS):设,若使得,则称为(1)式的帕累托最优解。所有帕累托最优解所组成的集合称为帕累托集合,记作
定义3. 帕累托前沿(Pareto Front,简称PF):PS在目标空间中多对应的像,称为帕累托前沿。
定义4. 弱帕累托最优(Weak Pareto Optimality):若不存在,使得(),则称为弱帕累托最优。
定义 5. 严格帕累托最优(Strict Pareto Optimality):若不存在,且,使得 (),则称为严格帕累托最优。
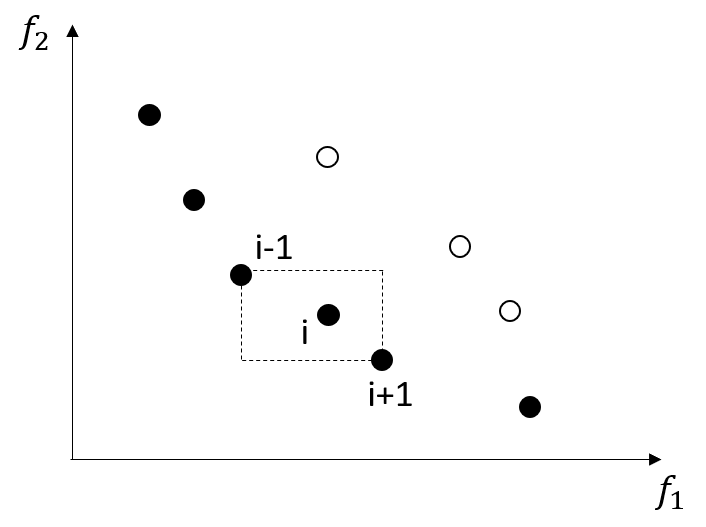
图1.1展示了一个二目标最小化问题目标空间中种群的分布。我们用这幅图来说明下帕累托支配关系。对于图中用红色标记的个体来说,它支配了区域2中的所有个体,且被区域3中的所有个体所支配。而区域1和区域4中的个体与其不存在支配关系。
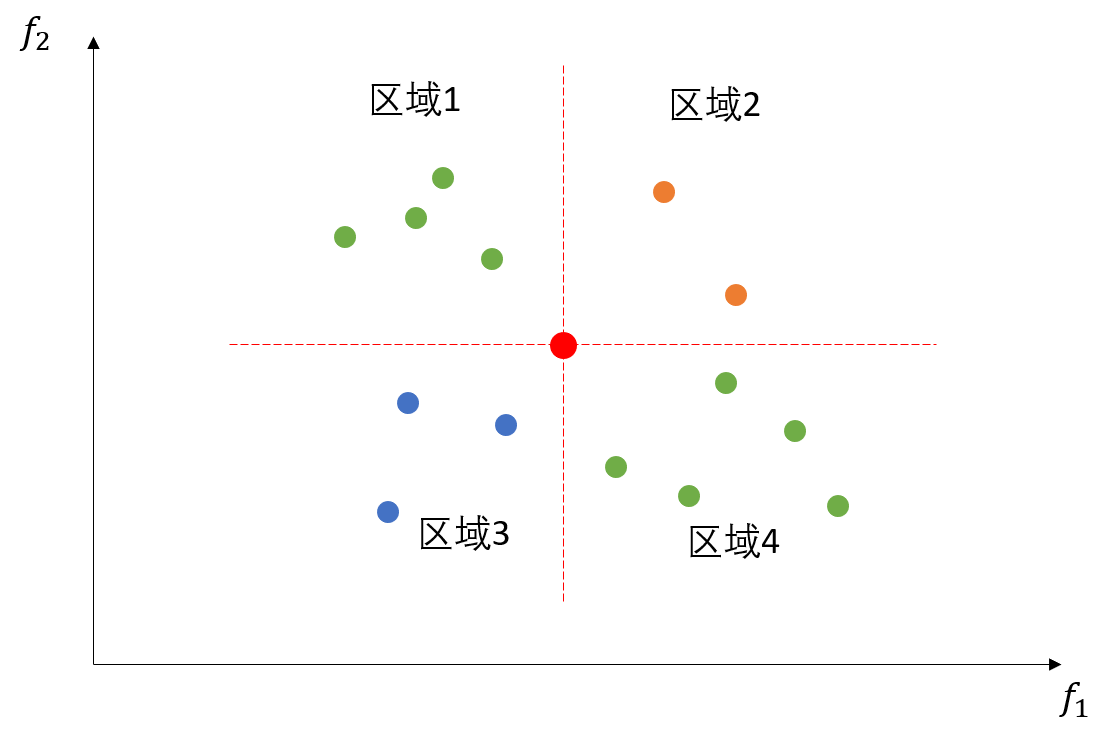
图1.1 帕累托支配关系
图1.2展示了一个二目标最小化问题的的一般形态,封闭曲线所围的区域为目标空间,红色段曲线即为。若将最小化问题改为最大化问题,则处于目标空间的右上角,如图1.3所示。为了方便求解,当遇到最大化问题时,只需要对该问题取负号,就可以将其转化为最小化问题进行求解。
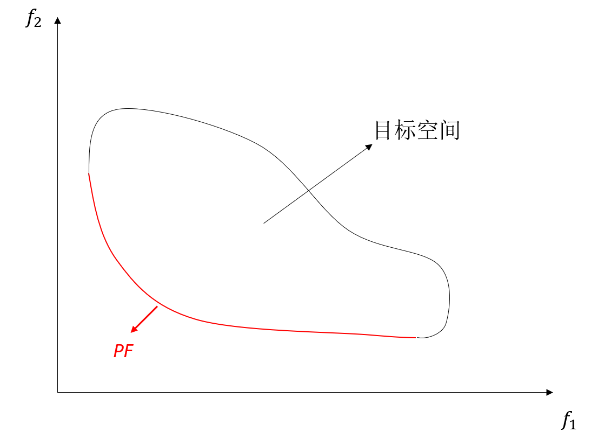
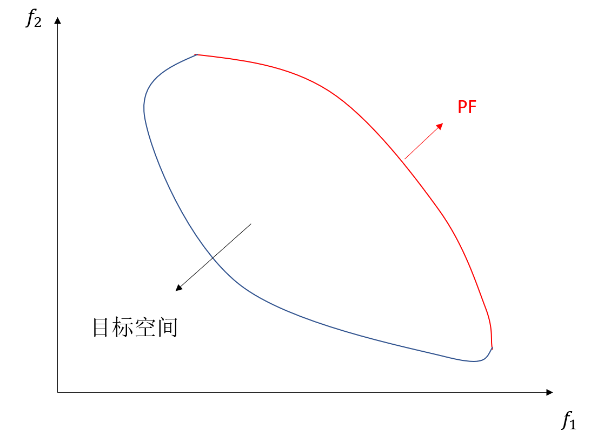
图1.2 二目标最小化问题的示例 图1.3 二目标最大化问题的示例
考虑到经典的多目标优化算法,例如基于加权和的方法(Weighted Sum Method)、-约束方法(-Constrained Method)只能找到单一的一个偏好解,近年来越来越多的研究者致力于使用基于种群的进化算法(Evolutionary Algorithms,EAs)来解决MOPs,我们称这类EAs为多目标进化算法(Multi-objective Evolutionary Algorithms,MOEAs)。在单目标进化算法中,N个个体最终会收敛到一个地方,表示同一个最优解。而在多目标领域中,通过初始化得到的N个个体在进化后仍为N个,表示帕累托集合。这也就是MOEAs的优势所在,可在一次执行中找到MOPs的帕累托集合。最早的MOEA是Schaffer等人于1985年提出的向量评价遗传算法(Vector Evaluated Genetic Algorithm,简称VEGA),虽然该算法存在很多的缺点,但是极大地推动了多目标优化领域的发展[2]。二十一世纪之后,多目标优化领域进入快速发展的时期,研究者们相继提出了许多收敛性好、多样性高且速度快的MOEAs,例如Nondominated Sorting Genet Algorithm II(NSGA-II)、Strength Pareto Evolutionary Algorithm2(SPEA2)、Pareto Envelope-Based Selection Algorithm II(PESA-II)、Multiobjective Evolutionary Algorithm based on Decomposition(MOEA/D)、Regularity Model-Based Multiobjective Estimation of Distribution Algorithm (RM-MEDA)[3-7]。随着优化问题决策变量数目和目标数目的增多,给优化造成了很大的困难,高维多目标进化算法(Many-Objecitive Evolution Algorithms)应运而生。然而纵观该领域近二十年的发展可以发现,研究者们的研究重点主要集中在算法设计上和算法应用上,很少有关于如何高效率地产生优质新解的研究,现有的MOEAs大部分都直接采用了传统的遗传重组算子,例如交叉算子和变异算子[7-8]。遗传重组算子是进化算法中的重要组成部分之一,一个高效率的遗传重组算子能使算法在尽可能短的时间内收敛到全局最优值处。随着所优化问题本身难度的增大,例如存在不确定性、噪音,搜索空间非常大,帕累托前沿不连续等,这些原本针对SOPs的遗传重组算子的效率显得十分低下。因此,有必要为日趋复杂的MOPs专门设计一个具备自适应性的遗传算子,通过学习种群的自身的性质,进行自适应的调整,以加快MOEAs的收敛。
1.2 国内外研究现状
目前,MOEAs主要可以分为以下三类:1)基于帕累托支配关系的MOEAs;2)基于分解的MOEAs;3)基于评价指标的MOEAs。2002年K.Deb等人提出的基于帕累托支配关系的NSGA-II是目前最经典的MOEAs之一,所提出的快速非支配排序也发展出了几个改进的版本,并成为许多MOEAs中的一个重要步骤[9]。2007年张青富等人提出了基于分解的MOEA/D算法,首次确定了分解的概念,自此产生了一系列基于MOEA/D框架的算法,如MOED/D-DE、MOEA/D-EGO等[10-11]。在此之前,虽然并没有明确分解法这个概念,但在许多算法中也能看到分解方法的身影,例如MOGLS、MOSA等,这些算法均用到了分解法的思想,将MOPs分解为一些单目标优化子问题,并同时对这些自问题进行求解[12-13]。2004年E. Zitzler等人首次提出基于指标的进化算法(Indicator-based evolutionary algorithm,IBEA),该算法使用任意一个评价指标去比较两个候选解,且没有使用额外的多样性保持机制[14]。Hypervolume(HV)指标是目前多目标优化领域内唯一一个关于帕累托支配严格单调的指标,因此引起了广大研究人员广泛的关注,提出了许多基于HV指标的算法。然而HV的计算代价十分大,尤其是当MOPs的维度达到六维及以上时。为降低HV的计算复杂度,J.Bader等人放弃计算HV的准确值,而尝试采用蒙特卡罗模拟法(Monte Carlo simulation)去估计HV的值[15]。经典的HypE(Hypervolume Estimation Algorithm for Multiobjective)就采用了这种思想,当目标维度较小时,采用精确计算HV的方式,而当目标维度较高时,采用估算法来计算[16]。HyPE在高维多目标优化问题(Many-objecitve Optimization Problems,MaOPs)上取得了很好的效果。
所谓的MaOPs一般指目标数超多3的多目标优化问题,目标数的增大给优化带来了许多困难。对于MaOPs来说,大量个体间不存在帕累托支配关系,选择压力小,因此基于帕累托支配关系的算法在处理MaOPs时往往效果不佳。目标维度的增大也大幅度的增加了评价指标的计算量,同时也使得帕累托前沿的可视化变得困难。K.Deb和H.Jain在NSGA-II的基础上提出了针对MaOPs的NSGA-III[8]。NSGA-III的基本框架与NSGA-II非常类似,但使用了一组分布均匀的参考点来帮助种群维持多样性,是一种基于分解的MaOEAs,这类算法的效果十分依赖于MaOPs的帕累托前沿的形状[17]。KnEA则通过引入拐点(Knee Point)作为第二选择标准来增大种群的选择压力[KnEA],但由于在很多情况下拐点可能并不存在,因此使用KnEA的效果其实并不是很好[18]。
分布式估计算法(Estimation of Distribution Algorithm,EDA)是进化计算领域中的一种新兴的计算模式。在EDA中,不存在杂交和变异等过程,而是使用统计信息对种群进行学习建模而后采样以产生后代,如此反复执行建模、采样操作,直到满足终止条件。由Baluja于1994年提出的针对变量无关的PBIL(Population based incremental learning)算法是公认的最早的EDA[19]。2008年张青富等人针对变量间相互耦合的多目标优化问题提出了一种基于模型规则的优化算法RM-MEDA,该算法利用局部主成分分析(Local Principal Component Analysis,Local PCA)对种群分割建模,在变量耦合的MOPs上取得了非常好的效果[7]。然而建模的计算复杂度显然要比传统的遗传重组算子大,因此RM-MEDA的效果虽然优异,但相较于其他的MOEAs计算量较大。张青富同时也指出,可以尝试使用其他机器学习技术代替Local PCA来进行建模,例如混合概率主成分分析等。RM-MEDA主要针对PS与PF维度相同的MOPs。然而很多MOPs的PF虽然是一个(m-1)维的流形(m为目标数),但PS却是一个高维的连续流形,因此无法使用RM-MEDA进行优化。针对这种类型的MOPs,周爱民等人又提出了一种基于概率模型的多目标进化算法MMEA以同时近似PS和PF[20]。2014年其又分析证明了几个经典的遗传重组算子在MOPs上的不足,改进了重组算子,并提出了基于分解和混合高斯模型的MOEAs,称为MOEA/D-GM[21]。
将不同的技术进行融合使用也是进化领域中常见的手段。其中将局部搜索法与MOEAs结合的方式称为memetic MOEAs。H.Ishibuchi与T.Murata于1998年提出的MOGLS(Multi-objective Genetic Local Search Algorithm)是最早的memetic MOEAs之一[12]。该算法将目标的权重和作为适应值函数,并对每个子解执行局部搜索。Sun.J等人将DE(Differential Evolutionary,差分进化)与EDA结合提出了DE/EDA算法。在DE/EDA中,一部分子解由DE产生,另一部分子解通过对概率模型采样得到,以此将全局信息与局部信息有效的结合了起来[22]。
实重组算子大致可以分为两类:1)以父代为中心的算子(parent-centric operators),例如SBX,PCX和FR(Fussy recombination)[23-25];2)以均值为中心的算子(mean-centric operators),例如BLX,UNDX和SPX[26-28]。使用以父代为中心的算子产生的解分布在父代解的周围,而使用以均值为中心的算子产生的解分布在以父代解均值的周围。
模拟二进制算子(Simulated Binary Crossover,SBX)由K.Deb,R.Agrawal于1995年首次提出,并与多项式变异算子(Polynomial mutation,PM )一起成为目前最为广泛使用的遗传算子之一[29]。SBX结构简单,局部探索能力强,且自身具备一定的自适应性,即在其他参数一样的情况下,两个父解相距越远所产生的子代离彼此远的可能性越高[23,30]。
除了以上算子外,DE算子与PSO(Partical Swarm Optimization,粒子群优化)算子也十分常用,尤其是DE算子展现出了非常优异的性能。R.Storn和K.Price首次提出DE算法,并列举了10个常见的变异策略,用DE / x / y / z这种形式来表示,其中x表示参与变异的向量是从种群向量中随机选取还是从种群向量中选择最优的,用rand或best表示; y表示使用的差分向量的个数为1个还是2个, z表示交叉方式,用bin或exp表示,如表1.1所示,将其中的bin改为exp就可以得到十种变异策略[31]。DE算法的框架与遗传算法非常类似,也包含交叉、变异、选择步骤,只是在交叉、变异上的表现形式与遗传算法中的不同,其具有算法简单、全局搜索能力强、在多峰非凸非线性优化问题上效果好等优点。PSO算法由J.Kennedy和R.C.Eberhart于1995年提出[32]。PSO算法模拟了鸟群的行为规律,利用种群中个体(粒子)间的协作和信息共享来寻求最优解,是一种典型的仿生物算法。为了找到最优解,每个粒子都会朝着他们之前到达的最好的位置(pbest)和整个种群曾到过最好的位置(gbest)移动。它原本是针对SOPs提出的一种进化算法,2002年C.Coello Coello与M.Lechuga将其扩展到MOPs领域,提出了MOPSO(Multi-objecitive PSO)[33]。在MOPSO中,gbest不再是单一的一个点(位置),而是通过轮盘赌选择法或竞标赛选择法等从种群的非支配解中选取的N个点(N为种群大小)。DE算子和PSO算子都可看作是基于拟梯度的算子。例如在DE算子中,子代
这是DE中的一种常见形式,F为预设步长,CR为交叉概率。差分向量可看作是种群的梯度。在梯度的引导下,种群向着最优解前进。DE算子对参数F较为敏感,因此不少研究人员围绕着参数F提出了一些自适应策略,以加强DE算子的性能。He.X等人首次在MaOEAs中使用进化路径(Evolution Path)来描述种群的移动及其趋势,并采用一种自适应机制自动调节DE的参数,以加快种群的收敛速度[34]。Keshk.M等人使用隐马尔科夫模型(Hidden Markov Model,HMM)来压缩中种群的信息,以自适应调整DE的参数[35]。除了直接调节算子的参数外,也有研究人员将不同算子结合使用。Zhu.Q等人在基因层面上将SBX算子与DE算子进行了结合,提出了AHX(Adaptive Hybrid Crossover)算子[36]。在进化的早期,算法更有可能选择使用DE算子,以加强全局搜索能力,而在进化的后期,则加大了对SBX算子使用的概率,以加强局部搜索能力。因此AHX既具有SBX的局部搜索能力又具备DE的全局搜索能力。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: