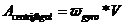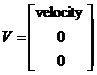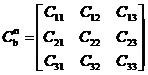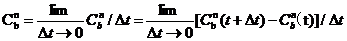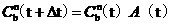基于腿部运动的机械臂运动控制毕业论文
2020-03-18 16:52:39
摘 要
本文简要介绍了关于工人在操作台工作时,往往会出现手不够用的情况,这种情况就需要机械臂的进行帮助。但如何控制机械臂来协助人的工作是个十分有意义的话题。本文期望通过人腿部的运动信息获取,设计人机交互界面,控制机械臂的动作,让机械臂成为工人的第三只手。通过使用惯性测量单元对于腿步运动的行为进行检测与数据采集。得到相应的角速度。之后得到位置数据。之后进行姿态解算得到相应指令控制进而作用到相应的机械臂上。
本篇论文通过机械臂模型的建立、力/位置混合控制算法、振荡抑制以及机械臂系统控制的仿真等方面进行设计并开展仿真研究,本次论文的设计在机械臂的控制理论及IMU传感器的使用方面具有重要的理论和实际意义。
关键词:惯性测量单元IMU,机械手,姿态解算与控制,人机交互界面
ABSTRACT
The paper gives a brief introduction about industrial workers in work station work, hand not enough use, often can appear to need help from the mechanical arm, how to control the mechanical arm to help man to work is an interesting topic. In this paper, we hope to obtain the motion information of the human leg, design the man-machine interface, control the movement of the manipulator arm, and make the robot arm become the third hand of the worker. In this paper, we use the inertial measurement unit to detect and collect the movement of leg movement. You get the corresponding angular velocity. And then you get the location data. After that, the attitude settlement can be controlled to the corresponding mechanical arm.This article from the mechanical arm mode.
This paper through the establishment of the mechanical arm model, force/position hybrid control algorithm, the vibration suppression and mechanical arm system control simulation and so on to carry on the design and simulation research, the paper design for mechanical arm control theory and the use of the IMU sensor is of important theoretical and practical significance.
Keywords: inertial measurement unit IMU, manipulator, attitude calculation and control.
目录
摘要 I
ABSTRACT II
第1章 绪论 1
1.1 研究目的及意义 1
1.2 国内外研究现状 1
1.3测量单元 2
第二章 腿部运动信息的采集 4
2.1 陀螺仪和加速度计(特性分析) 4
2.2姿态的表示方法 9
2.3基于加速度梯度下降法进行姿态的求解 12
2.4融合算法进行姿态求解 16
第3章 试验与测试 19
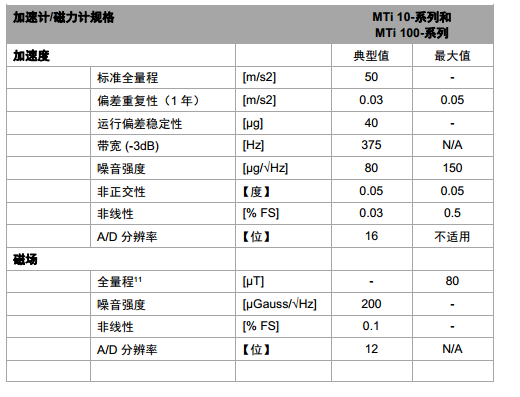
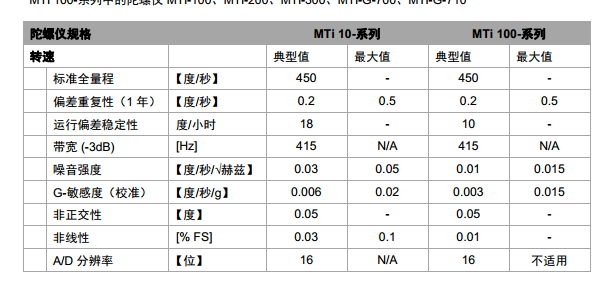
3.1运用的IMU介绍 19
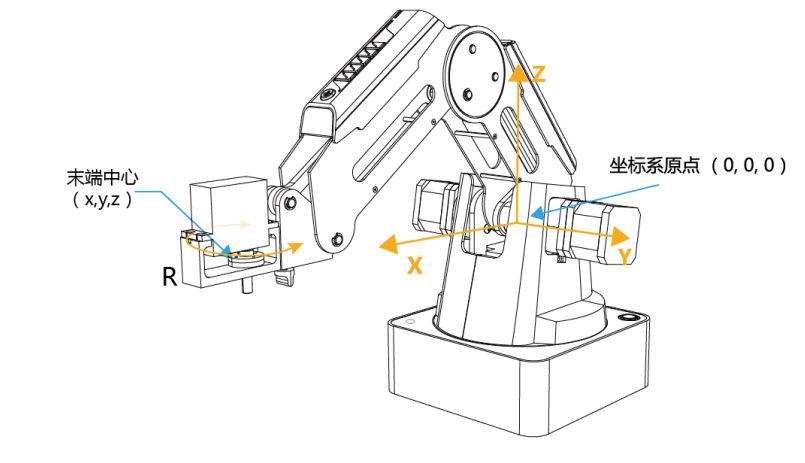
3.2机械手的介绍 20
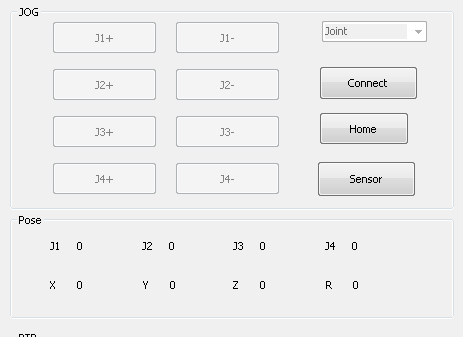
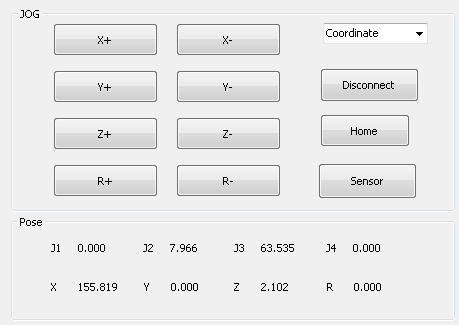
第4章 结果与仿真 22
4.1机械的接入与运行 22
4.2结果分析 23
第5章 结论与总结 24
参考文献 25
致谢 27
第1章 绪论
1.1 研究目的及意义
伴随着高速发展的社会,人们对于自动化半自动化的需求也在飞速增加,随之而来的问题就是对于人的提出了越来越高的要求,那么就需要人们多一个手臂,就是机械臂的运用。为了达到目的,就对于机械臂也提出了越来越高的要求。需要让它来完成越来越高级的操作。当然智能化机器人手臂也当然存在着较大的市场价值,所以我们对其进行智能化设计。可以通过一定的控制指令进行控制,使它成为人的第三个手臂,来完成更多人们在高危高压的环境下无法进行的操作。当在操作台工作时,往往会出现手不够用的情况,需要机械臂的帮助,如何控制机械臂来协助人的工作是个有趣的话题。本论文期望通过人腿部的运动信息获取,设计人机交互界面,控制机械臂的动作,让机械臂成为工人的第三只手。为工业实现半自动化起到了重要作用。
1.2 国内外研究现状
为了实现腿部运动的控制,人机交互界面的建立是最重要的一环。人机界面是人与机器进行交互的终端设备,人机界面是指人和机器在信息交换,和功能上接触,或者二者进行互相影响的领域称为界面,是工业自动化控制系统不可或缺的功能单元,主要包括文本显示器和触摸屏。文本显示器是一种单纯以字符形式呈现的人机界面,文本显示器因采用键盘输入、色彩单一且屏幕显示范围较小,多适用于经济型自动化设备。触摸屏是一种以字符和图形结合呈现的人机界面,画面切换及参数输入均直接在屏幕上进行,操作简单直观、图形和色彩丰富、功能多样,多适用于中高端自动化设备。如图1.2.1就是一个人机交互界面:
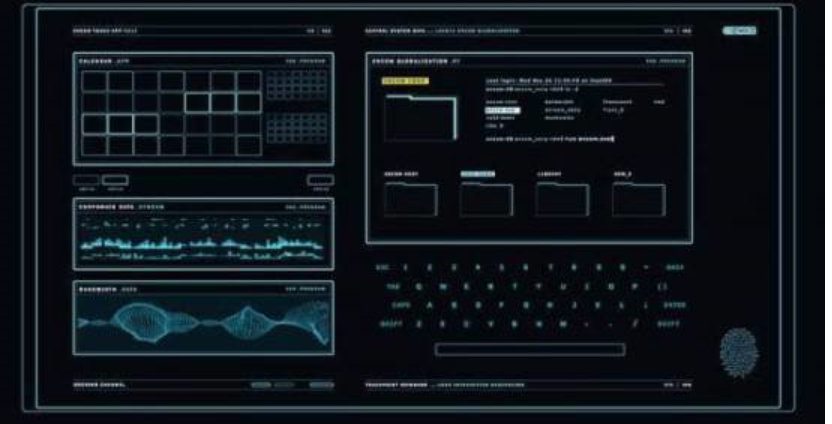
图1.2.1
现在人机交互界面通过考虑人们的需求与行为等多个方面,来确保交互界面的实用性。现有的人机交互功能与多方面因素有关,例如可用性,市场金融等。现在被大量应用的多是纯命令/动作设置,而不是复杂的物理设备。现在也进行了智能与自适应交互设计,此类的设计正在进行设计过程中部分,正处于摸索阶段。对语音输入由机器本身进行识别,而减少了对于手的输入操作。对于新一代接口的一个重要的发展方向是区分智能方式,界面和用户交互,智能人机交互设计界面,将至少从某种智能感知响应用户。
1.3测量单元
(英文:Inertial measurement unit,简称 IMU)是测量物体三轴姿态角(或角速率)进而得到加速度的一种传感器设计。为了提高系统的相对可靠性,我们可以在装置内为每个轴配备更多的更精确的传感器。安装在被测物体的重心上的IMU可以进而得到最准却的数据。
通过使用三轴加速度计与地磁轴相结合,外力的加速作用影响与作用下。在运动/振动环境中,输出方向角存在着较大的误差。此外,地磁传感器当然也存在着明显的缺点。由于地磁场的磁场线是它的绝对参考。地磁的特点是使用范围大,但由于强度低,大约有几个高斯的大小,所以他的磁场很不稳定,很容易受到其他磁体就算很小的磁场的的干扰。所以我们通过在里面增加了Z轴陀螺仪的瞬时角的方法,这样就可以使系统数据便可以做到更加稳定并且不易受到环境的干扰。加速度可以做到测量重力的方向的作用。如果没有外部加速度,它便可以稳定成功的准确的输出滚/纵轴两轴姿态角的大小,而这个角度也不会存在累积误差。它在较长的工作时间范围内更准确。然而,角加速度传感器测量也存在缺点,便是,加速度传感器实际使用MEMS技术检测时会时而产生了变形从而引起的一定的惯性力,其本质和重力是基本上一致相同的,所以加速度计无法做到去区分重力加速度与外力加速的系统的差别。当你做变速运动在三维空间中,其输出也会因为此类原因产生不正确的结果。
第二章 腿部运动信息的采集
为了实现腿部对于机械臂的控制,我们首先需要得到对腿部运动进行惯性测量单元的运用进而得到腿部的运动信息。那么我们就可以运用IMU得到传感器坐标的加速度,对得到的加速度转化为大地坐标系的加速度。对加速度对时间进行二次积分得到腿部在大地坐标系下的位移信息。进行坐标系的转换操作时我们需要在之前得到姿态的信息,那么我们就需要对imu的姿态求解方法,姿态的表示方法进行进一步的了解。
2.1 陀螺仪和加速度计(特性分析)
灵敏度是用来测量角速度进而描述机器指标的数据,是一个装置的使用与运行的关键参数之一,具有着出色的运动学特性的特点,间接也可以完成测量角度的任务,所得到的数据为陀螺灵敏度(单位为毫伏/秒,速度转换为电压值)的数据参考,但是他的测量范围较小,因为气体灵敏度也会得到更好的效果,所以得到了更普遍的应用。从另外一句话说,它其实是角对于时间进行求导操作得到,从而得到的也就是角速度,反过来角速度与时间俩个数据的给出也可以通过计算得到它的角度数据。陀螺仪是陀螺灵敏计内部的一个重要组成元件,它的轴需要与初始运动方向相平行,才可以得到较为准确的数据,那么我们就可以通过从初始方向的偏差来计算旋转的方向和角度。
谈及加速度计,较高的低频特性是他的一大特点,所以可利用这个来进行低速静态加速度的检测。在无人机上可有应用,那就是可完成重力加速度g的测量和分析等,当加速度计进行自由旋转时,也就是开始进行测量工作时,三个轴上的重力加速度分量值便可以展现在我们的眼前。我们对得到的数据进行分析解算,那么平面与地面之间的夹角就可以使用加速度即成功地得到。测量并得到重力加速度,三轴加速度计输出重力加速度的分量等相关数据这些工作只需要使用加速度计来完成。在加速度计的体坐标系的三个方向的坐标轴上,重力加速度是具有固定的大小和方向。通过借助这个法则,我们就可以借助这一
点得到加速度计所在平面与地面之间的夹角关系。倘若加速度计以重力加速度的轴进行旋转运动,测量值是保持不变的,换句话说就是加速度计不能感知这个水平方向的旋转。姿态解算方法的比较:
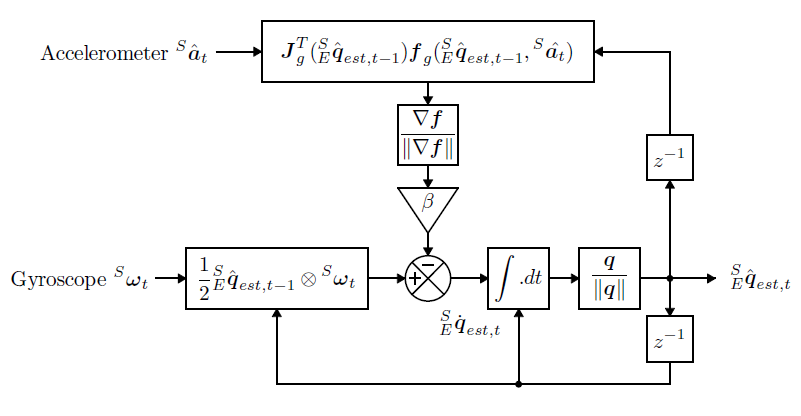
上述算法都是来减少修正陀螺仪的误差的,算法是使用了PI反馈控制器实现反馈修正的加速度计和磁力计修正陀螺仪的误差。如图2.1.1
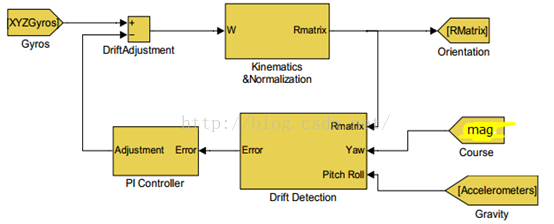
图2.1.1
第一步,我们建立坐标系,我们令东北天坐标系为n系(地理坐标系,参考坐标系),零载体坐标系为b系,飞行器的坐标系成功的建立了出来。之后我们进行四元数法的姿态解算,进行最重要的四元数的值的求取;我们建立方向余弦矩阵(用于表示n系和b系的相对关系)对其中的元素进行分析计算得到数据,但是数据为三角函数,使用四元数法需要得到四元数,所以矩阵中的元素便需要进行转换运行。姿态解算的实质,其实就是为了能够由四元数构成的方向余弦矩阵nCb(前面俩个数据都是具有转置关系的)进行求解计算。
通过对之前的数据进行分析,不难发现上述矩阵得到后他的误差就是不可以被避免的。但是如果想对于一个变量进行不同的坐标系的表示那么也很难实现,在每个不同坐标系力所表示这个变量的大小和方向就肯定是相同的。如果无法完成就无法成功的实现接下来的运算过程[17]。但是现在就出现了这个误差问题就是由于这两个坐标系的转换矩阵所导致.我们接下来进行误差的消除运算,首先队医一个向量经过这么一个有误差存在的旋转矩阵变换计算进行转换,在另一个具有偏角的坐标系中我们得到的数值便产生了与我们初始数据存在误差的结果,得到误差后,通过对这个偏差进行分析计算的方法来进行修正工作,最后达到修正这个旋转矩阵的误差的目的。记得这个旋转矩阵的元素需要使用为四元数,换句话说我们需要修正的或者是整个运算过程也是四元数,得到四元数后使用四元数法一步一步的把姿态进行修正,姿态解算的基本原理大概就是这样。姿态解算完成后四元数类型的数据便得到了呈现,在之前描述的运算过程其实时使用四元数的,但是这个方法存在
局限性,通过加速度计和地磁计来修正姿态的操作就不是值得可取的方法,加速度计和地磁计在整个运算中担任简单的测量工具和载体的任务,但是使用这两个器件数据也可以得到了旋转矩阵的误差存在,然后通过进行修正计算,使用四元数算法达到修正误差的目的,进而修正四元数,最后得到正确的姿态。
加速度计可以进行修正,考虑离心加速度这个因素是实现这个运算的必要因素。离心加速度在这里与旋转率向量和速度向量的交叉乘积的数据是相同的。我们在这里假设飞机方向和X轴平行。
| (2.1) |
| (2.2) |
在机体上我们使用器材测得的重力为:Pitch_roll的旋转修正向量是由DCM的Z行进行归一化计算以后的重力参考向量的交叉乘积。
| (2.3) |
我们分析n系,加速度计进行一定的输出,经过bCn(用四元数表示的转换矩阵)平面对于平面进行转换之后进而得到了xb的值,对于b系中的各个因素进行分析,加速度计对于其进行测量得到cb,在此之后我们把得到的值转化为b系中竖直向下的方向中。之后,对此我们进行叉乘操作,来得到系中所存在的误差。对于此误差进行分析进而得到更加完善的bcn矩阵中。在这样的计算过程中我们便可以通过四元数法进一步地修正过程。但是,加速度计也存在着缺点就是无法进行z轴上的旋转运动进行感知。所以地磁计应用就是不可缺少的了[7]。
在静止时加速度计所测量的就是重力加速度,他是具有大小与方向的量。当然我们也可以推理到地磁计测量的大小也是具有大小和方向的。但是他不是完全竖直向下的。它与x轴存在着一定的偏离角,或者是与z轴有一个倾斜角度的。在n系中,加速度计对此坐标系的方向向量是恒定不变的,但是我们使用地磁计就无法保证这个条件。那么我们要得到bx,bz的准确值就在通过加速度计的补偿与修正运算来得到,而是通过地磁计与陀螺仪的使用来进行姿态运算进而得到我们需要的修正目的。但是使用这种方法的相关技术仍然不是很成熟,那么我们进行姿态解算时就需要得到bx与by。我们可以进行旋转坐标系的操作来得到较为准确的数据,如图2.1.2所示。通过图中不难看出使用四元数法来进行任意角度的旋转都是可以实现的,需要计算的只是偏航角的大小这个误差也是导致加速度计无法修正偏航的原因[16]。
。
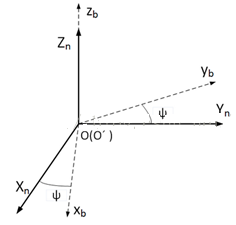
图2.1.2 坐标系
现在我们进行反推得到,从b系推往n系:设地磁计在b系中的输出[mx.my.ma]T经过Co1平面进行旋转之后得到[hx.hy.he]T(n系。在这个0r平面上就变为了m系),[bx.0.bz]T的投影为sqrt((hx*hx) (hy*hy))。很明显的是,地磁计在XOY平面上(n系)的向量的大小是保持不变的,那么我们就可以有bx=sqrt((hx*hx) (hy*hy))。当对于bz进行数
据处理,我们使用同样的方法,只需要令bz=hz即可。经过同样处理方法之后就可以得到[bx.0.bz]T,经过BCn1平面旋转就可以成功回转到b系中,[wr.wy.wa]T便成功的得到了,这个值再进行下一步计算就是和b系中的地码计输出[mL.my.mu]T进行向量积来得到一定误差,进行再次修正bCn1 (或者:nCb1),就得到bCn2 (或者:nCb2)。上述操作就成功完成了一次地磁计的补偿操作[8]。
加速度计又是无法完成z轴上的旋转修正的任务,那么就可以通过地磁计在XOY平面上的地磁力相同原理就行修正操作,从而得到了z轴的修正[9],然后在这个基础之上,该地部计补偿方法当然必须依照重力加速度计进行修正来得到提供一致的X0Y平面的目的这样,才产生了bx=sqrt((hx*hx) (hy*hy),使这一个式子成立,yaw我们通过使用地磁计来进行补偿,最终得到了没有偏差的实时姿态。 对Gyro修正补偿以后为:
w(t)=wgyro(t) wcorrection(t)
wgyro(t)=three axis measurements
wcorrection(t)=gyro correction (2.4)
并把通过PI反馈控制器修正过的grow vector作为公式的输入更新DOM:
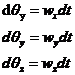
(2.5) |
主要分析一下该算法的实现,可以通过该失量左乘方向余弦矩阵Cnb转换到参考系中: rn=Cnb.*rb
(2.7) |
| (2.6) |
方向余住矩阵随时间的传弗的推导过程。C随时间的变化率(标红表示更新后的)如下:
| (2.7) |
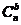 (t
(t 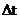 )可以写成加下两个矩阵相乘的形式:
)可以写成加下两个矩阵相乘的形式:
|
| (2.8) |
式中A(t)是一个联系b系从t时刻到t △t时刻的方向余弦矩阵。对于小角度转动,A(t)可以表示为: A(t)=[I △A), 其中1是3*3的单位矩阵。且
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: