基于RRT的路径规划算法研究毕业论文
2020-02-19 07:53:31
摘 要
在自主移动机器人的路径规划问题中,快速拓展随机树算法(rapidly-exploring random tree , RRT)是常用的算法之一。但RRT算法寻求的可行路径往往存在路径不具有最优性的问题,因此有学者在RRT算法的基础上,提出一种改进的RRT*算法,使所得可行路径具有渐进最优性。本文旨在将RRT*算法与RRT算法进行实验对比,分析RRT*算法相对于RRT算法在路径最优化上的改进程度。其次,为了加快算法的收敛速度,又对RRT*算法增加了目标偏向策略,同样地对RRT*算法和增加了目标偏向策略的RRT*算法进行对比实验,分析它们在收敛速度上的差距。所有的仿真实验均在MATLAB平台上完成,使用RRT算法、标准RRT*算法和增加了偏置概率P的RRT*算法分别对不同类型的地图进行多次测试,记录三种算法的时间代价与路径代价,对比所得数据,具体分析三种算法各自的优势与缺点。
关键词:自主移动机器人;路径规划;RRT算法;RRT*算法;目标偏向策略。
ABSTRACT
In the path planning problem of autonomous mobile robots, the rapid-exploring random tree (RRT) algorithm is one of the commonly used algorithms. However, the feasible paths sought by RRT algorithm often have the problem that the paths are not optimal. Therefore, on the basis of RRT algorithm, some scholars propose an improved RRT algorithm--RRT* algorithm, which makes the feasible paths have asymptotic optimality. This paper aims to compare the RRT* algorithm with the RRT algorithm and analyze the improvement of the RRT* algorithm relative to the RRT algorithm in path optimization. Secondly, in order to speed up the convergence of the algorithm, the target bias strategy is added to the RRT* algorithm. Similarly, the RRT* algorithm and the RRT* algorithm with the target bias strategy are compared to analyze their differences in convergence speed. All simulation experiments were performed on the MATLAB platform. The RRT algorithm, the standard RRT* algorithm and the RRT* algorithm with the added bias probability P were used to test different types of maps separately. Record the time cost and path cost of the three algorithms, then compare the data we got and analyze the advantages and disadvantages of each of the three algorithms specifically.
Key Word : Autonomous mobile robot ; path planning ; RRT ; RRT* ; Target bias strategy.
目录
摘要 I
ABSTRACT II
第1章 绪论 1
第2章 算法分析 3
2.1问题分析 3
2.2标准RRT算法分析 3
2.3标准RRT*算法分析 5
2.4加入偏置概率P的RRT*算法分析 8
第3章 MATLAB仿真分析 12
3.1仿真环境地图的建立 12
3.1.1实验地图的设定与仿真平台介绍 12
3.1.2无障碍地图 12
3.1.3多通路圆形障碍地图 12
3.1.4单通路复杂迷宫图 13
3.2实验结果对比分析 13
3.2.1无障碍地图 13
3.2.2多通路圆形障碍地图 16
3.2.3单通路复杂迷宫图 19
第4章 结论与展望 23
参考文献 25
致谢 26
附录 27
第1章 绪论
机器人技术是一项综合性的应用技术,它涉及的学科领域极其广泛,像机械、模式识别、自动控制以及人工智能等。而在机器人的研究中,机器人的自主移动又是一个非常重要的研究方向,它包含了运动学、信息论和信号分析等相关知识。目前,自主移动机器人不仅在宇宙探索、海洋开发、原子能等高精尖领域内发挥作用,在军事、工业、农业、服务业等诸多行业领域中也得到了广泛的应用。自主移动机器人具有广阔的发展前景,展现出了巨大的发展潜力。
能否找出合适的移动路线并成功的通过移动路线完成任务目标是自主移动机器人的一个重要性能指标。这就是自主移动机器人的路径规划问题。自主移动机器人的路径规划是指按照一定的评价标准,智能地决策出一条从起始位置到目标位置的无碰撞路径[1]。
在解决路径规划问题时,往往需要考虑很多因素,其中比较重要的因素有环境的不确定性和规划算法的有效性与最优性[2]。在实际应用中,神经网络和遗传算法等是国内外学者们常用的方法,但这些算法也都还存在着一些缺点,尤其是在算法的实时性和收敛速度方面,因此在实际应用中很难满足系统对效率的高要求。除此之外,这些算法都还需要预先对所处空间环境进行处理,需要了解整个空间的构成状态,障碍物的位置等,然后对整个环境空间进行建模,如果所处环境比较复杂,自主移动机器人的自由度也比较高,那使用这类算法就会特别繁杂,难度非常大。而D*、PRM等算法在搜索路径时虽然能够满足最优性和实时性的要求,但是它们未考虑车辆非完整性约束的限制,导致了自主车不一定能跟踪连通的路径[3]。
美国爱荷华州立大学 Lavalle 教授于1998年提出了快速搜索随机树(Rapid-exploring Random Tree,RRT)算法。RRT算法的主要原理是在所处状态空间中不停的生成随机采样点,并将这些采样点有序的连接起来,与状态空间进行碰撞检测,保留下合适的采样点。算法对整个空间环境的碰撞检测就可以直接得知空间内障碍物区域与空白区域的位置,从而了解地图的构成,继而在空白区域内寻找一条连接起始点和目标点的可行路径。这种方法可以有效避免对复杂空间的建模,而且不需要事先进行其他处理,因此,RRT算法在近年来的机器人运动规划领域中得到了广泛的应用和研究。但是RRT算法也并非无懈可击,也正是由于它所采用的随机采样方式,使得算法对空白区域的搜索非常平均,所以最终得到的可行路径往往都不是最优路径,与最优路径有所偏差。即算法不具备路径最优性[4]。
为了弥补标准RRT算法的不足,国内外众多研究学者提出了许多对RRT算法的改进方案。例如:双向搜索树(bi-RRT)[5];RRT-Connect算法[6];Forage-RRT算法[7];杂波环境下的IRRT算法[8]等。
2011年,Karaman和Frazzoli等人针对RRT算法不具备最优性的缺点,提出了一种改进的RRT算法——RRT*算法,相比于标准的RRT算法,RRT*算法引入了ChooseParent过程和Rewire过程来实现算法的渐近最优性[9]。该算法在不限制迭代次数与运行时间的情况下,在概率上能100%的找到最优路径[10]!因此它不仅仅继承了RRT算法的概率完备性,还重新具备了渐近最优性。但是由于加入了ChooseParent过程和Rewire过程,它的计算也更为复杂,为找寻到合适的可行路径,RRT*算法需要耗费很多的时间去进行代价的计算。因此,它渐近最优性的实现是以舍弃收敛的快速性和加大搜索时长为代价的。
RRT*算法虽然实现了渐进最优性,但它舍弃了算法收敛的快速性,为了能够两全其美,在不舍弃算法收敛快速性的情况下实现渐进最优性,在参考其他文献后决定在标准RRT*算法的基础上加入目标偏置策略[11]。目标偏置的思想主要体现在新采样点的选择上,标准RRT*算法的新采样点是随机生成的,这个随机性使得算法可以自由探索环境空间,但也影响了算法的收敛速度,所以我们可以适当地降低新采样点生成的随机性,让算法在一定概率下将新采样点定为目标点,使算法向目标方向移动,以实现目标偏置思想。目标偏置策略可以降低算法搜索不必要空白区域的概率,加快随机树T的收敛速度,有效地改善RRT*算法收敛速度慢、搜索时间长的缺点。
本文的主要研究内容包含两个方面:一是标准RRT*算法相对于RRT算法在减小路径代价方面改进的程度和时间代价增加的程度;二是增加目标偏置策略P后的RRT*算法相对于标准RRT*算法在减小时间代价上的改进程度和对标准RRT*在缩短路径方面的影响。
本文的仿真实验,主要是通过MATLAB软件对三种不同的算法在多种不同类型的相同地图上进行测试,多次仿真实验后,分别记录RRT算法、标准RRT*算法和添加偏置概率P后的RRT*算法在每张地图上所找寻到的可行路径的时间代价与路径长度,对所得数据进行对比分析,具体的了解三种算法各自的优势与劣势,分别适用于哪种环境空间下。
本文的内容安排如下:
第一章:绪论。主要介绍项目的研究背景、发展现状与发展前景,对文章内容的规划。
第二章:算法分析。对三种不同的算法原理进行分析。主要包含的小节有:(1)标准RRT算法分析;(2)标准RRT*算法分析;(3)加入偏置概率P的RRT*算法分析。
第三章:对三种算法进行仿真实验,对所得数据进行对比分析。主要包含的小节有:(1)仿真环境地图的建立;(2)实验结果对比分析。
第四章:对本文所做工作进行总结,并对今后的研究提出展望。
在文章的最后,对所有提供了帮助的老师、同学、领导以及家人诚挚的致以谢意!
第2章 算法分析
2.1问题分析
假设整个地图区域为M,MobsM表示为障碍区域,Mfree M表示为无障碍区域,Mfree ∪ Mobs = M且Mfree ∩ Mobs = ,Xstart ∈Mfree为起点,Xgoal ∈ Mfree为目标点。算法需要找出一条连接起点和终点的路径且该路径与障碍区域无碰撞。
2.2标准RRT算法分析
RRT算法能够迅速的搜索整个构型空间,主要思想就是通过分裂环境地图来访问构型空间中未被拓展的部分。RRT算法不同于图搜索算法,它通过在全图中不断随机撒点,将路径像树一样延伸直至终点,这样它不需要对环境进行建模,很适合在动态环境下快速开拓路径。实际上,RRT算法正是维护树状结构的过程[12]。
下面对RRT算法的基本原理进行分析:
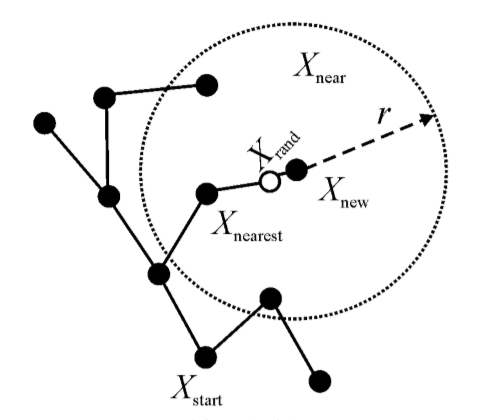
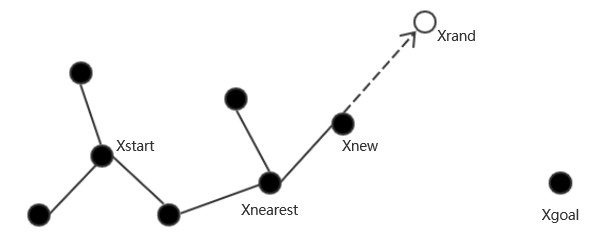
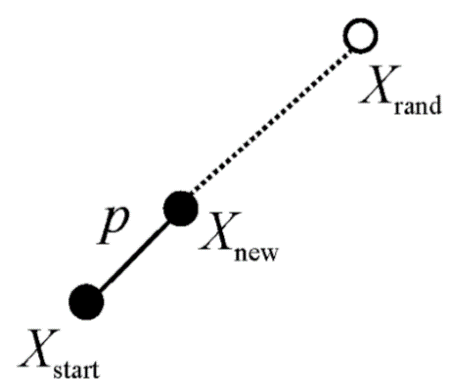 首先将起点Xstart作为随机树T的初始节点,然后在整个环境空间内进行随机采样,获得一个随机点Xrand∈Xfree,接着遍历随机树T的所有节点,找到随机树T中距离Xrand最近的一个节点Xnearest,在直线XnearestXrand上找寻一点Xnew,使线段XnearestXnew的长度等于搜索步长p,如果线段XnearestXnew与障碍区域没有任何接触,则保留Xnew点并加入随机树T,成为新的节点;否则舍弃Xnew点,进入下一次迭代,如图2.1所示。
首先将起点Xstart作为随机树T的初始节点,然后在整个环境空间内进行随机采样,获得一个随机点Xrand∈Xfree,接着遍历随机树T的所有节点,找到随机树T中距离Xrand最近的一个节点Xnearest,在直线XnearestXrand上找寻一点Xnew,使线段XnearestXnew的长度等于搜索步长p,如果线段XnearestXnew与障碍区域没有任何接触,则保留Xnew点并加入随机树T,成为新的节点;否则舍弃Xnew点,进入下一次迭代,如图2.1所示。
图2.1 生成Xnew节点
如此反复进行迭代,直到Xnew落入Xgoal一定范围内,则认为路径搜索成功,结束迭代并输出所找寻到的路径,如图2.2所示。
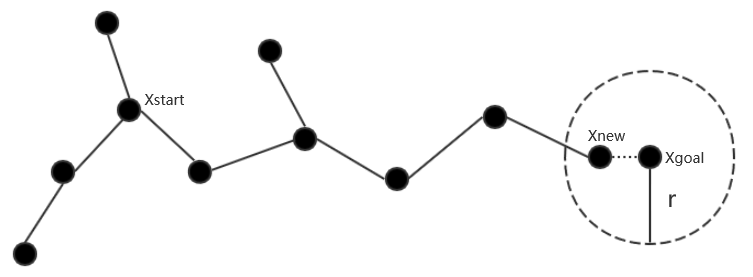 图2.2 路径找寻成功
图2.2 路径找寻成功
标准RRT算法的伪代码如表2.1所示:
表2.1 RRT算法伪代码
步骤 | 伪代码 |
1 | T←InitializeRRTTree() |
2 | InitNode(Xstart,Xgoal,T) |
3 | for i=1 to i=N do |
4 | Xrand←Sample(i) |
5 | Xnearest←NearestNode(T,Xrand) |
6 | Xnew←NewNode(Xnearest,Xrand) |
7 | if Free(Xnew) then |
8 | T←IntNode(Xnew,Xnearest,T) |
9 | if Closer(Xnew,Xgoal) then |
10 | return T |
由RRT算法的原理可知,RRT算法倾向于拓展到开放的未探索区域,只要时间足够,迭代次数足够多,没有不会被探索到的区域。所以只要有至少一条可行的路径,RRT算法都必定可以找寻到它,即RRT算法具有概率完备性。
但RRT算法也并不是完美的,由于RRT算法是在全局区域盲目的寻找搜索,搜索路径策略是基于随机采样的搜索,因此会在不必要的无障碍区域生成很多节点,浪费很多不必要的时间;其次,RRT算法并不追求所得可行路径最优化,所以RRT算法所得的可行路径一般长度较长,即路径不具有最优性。
2.3标准RRT*算法分析
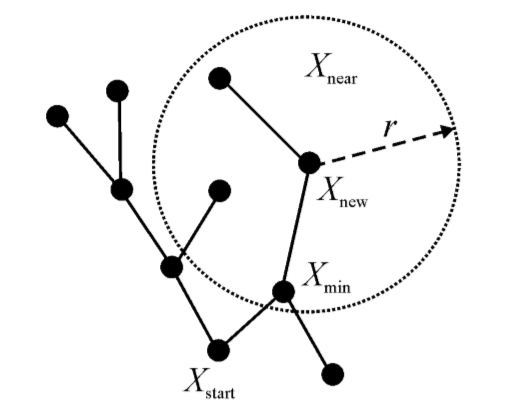
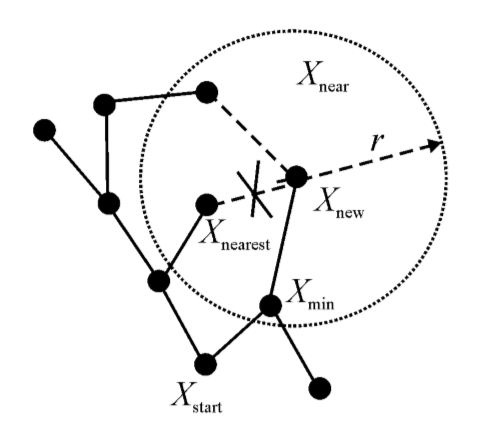
为了解决路径最优性的问题,RRT*算法应运而生。RRT*算法是在RRT算法基础上进行的改进,目的是为了使所得的可行路径具有渐进最优性。渐进最优的RRT*算法在原有的RRT算法上,改进了父节点选择的方式,采用代价函数来选取拓展节点领域内最小代价的节点为父节点,同时,每次迭代后都会重新连接现有随机树上的节点,从而保证计算的复杂度和渐进最优解[13]。
下面对RRT*算法原理进行分析:
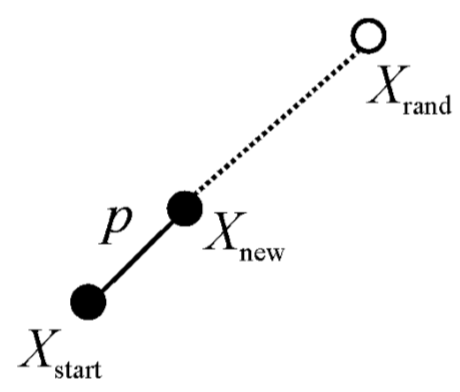 第一阶段:首先将Xstart作为随机树T的初始节点,然后在整个环境空间内进行随机采样,获得一个随机点Xrand ∈ Xfree,接着遍历随机树T的所有节点,找寻到离Xrand最近的节点Xnearest,在直线XnearestXrand上找寻一点Xnew,使线段XnearestXnew的长度等于搜索步长p,如果线段XnearestXnew与障碍区域没有任何接触,则连接线段XnearestXnew,保留Xnew点并加入随机树T中,如图2.3所示。第一步与RRT算法没有太大差异,都是对随机树新节点的获取与判别;
第一阶段:首先将Xstart作为随机树T的初始节点,然后在整个环境空间内进行随机采样,获得一个随机点Xrand ∈ Xfree,接着遍历随机树T的所有节点,找寻到离Xrand最近的节点Xnearest,在直线XnearestXrand上找寻一点Xnew,使线段XnearestXnew的长度等于搜索步长p,如果线段XnearestXnew与障碍区域没有任何接触,则连接线段XnearestXnew,保留Xnew点并加入随机树T中,如图2.3所示。第一步与RRT算法没有太大差异,都是对随机树新节点的获取与判别;
图2.3 首次拓展子节点
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: