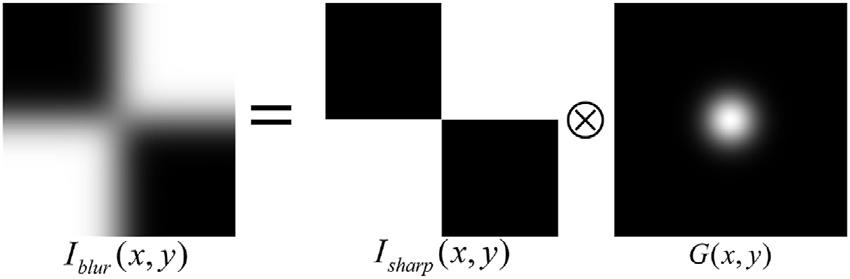基于相位靶的相机标定方法研究毕业论文
2020-02-19 07:53:22
摘 要
传统的相机标定方法通常需要清晰的标靶图案来做准确的特征提取。为了寻找一种简单、有效、精度高,并且在摄像机离焦状态下也可以精确标定的摄像机现场标定方法,提出将已知周期的平面二维圆阵列作为标定平面靶,通过傅里叶二维图案分析方法,得到两个正交的包裹相位图,并由此提取特征点坐标,通过其与平面坐标的对应关系可以建立图像坐标与2D平面标靶坐标的一一对应关系。将此平面二维圆阵列靶在摄像机的成像空间中放置不同的位置,在不同视角拍摄多张照片,并完成相位测量,然后根据2D共面参照物摄像机标定方法即可完成摄像机标定。此方法利用相位而不是强度分布提取特征点,并且不需要多帧图案,实验和计算机模拟证明,此方法简单可靠精度高,即使在严重离焦状况下也能获得精确的标定结果。
关键词:相机标定;平面二维圆阵列;傅里叶变换;离焦;特征提取;
Abstract
Traditional camera calibration methods always require sharp target images for accurate feature detection. In order to find a camera calibration method that is simple, effective, high precision, and can be accurately calibrated under the defocus state of the camera, a planar two-dimensional circular array with a known period is proposed as a calibration plane target, and Fourier two-dimensional is adopted. The pattern analysis method obtains two orthogonal parcel phase maps, and extracts the feature point coordinates, and the one-to-one correspondence between the image coordinates and the 2D plane target coordinates can be established by the correspondence relationship with the plane coordinates. The planar two-dimensional circular array target is placed in different positions in the imaging space of the camera, multiple photos are taken at different viewing angles, and phase measurement is completed, and then the camera calibration can be completed according to the 2D coplanar reference camera calibration method. This method extracts feature points using phase rather than intensity distribution, and does not require multi-frame patterns. Experimental and computer simulations show that this method is simple, reliable, and accurate, and can obtain accurate calibration results even under severe defocus conditions.
Key words: Camera calibration;2D circular array target ;Fourier transform;Out-of-focus;Feature detection
目录
第一章 绪论 1
1.1研究背景 1
1.2国内外研究现状 2
1.3本文的研究内容 3
第二章 理论背景 4
2.1相机模型 4
2.1.1线性模型 4
2.1.2非线性模型 6
2.2张正友标定法简介 8
2.2.1参数求解 8
2.2.2结果优化 10
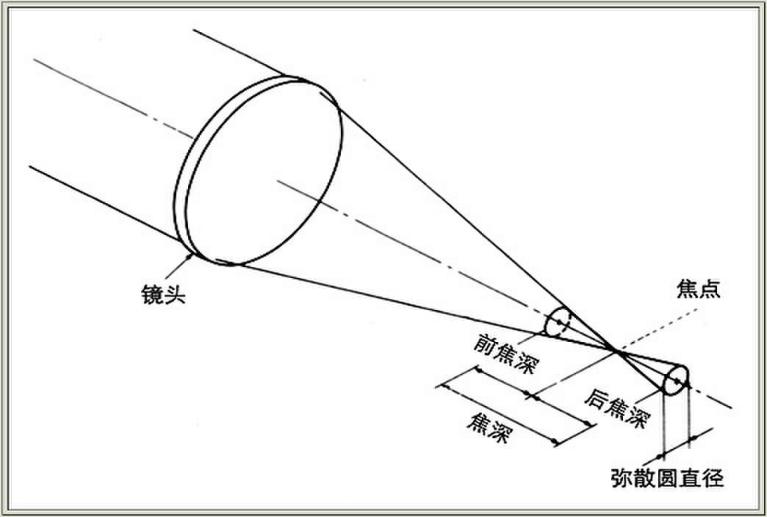
2.3相机离焦模型 11
第三章 离焦摄像机标定 13
3.1相移法求取特征点 13
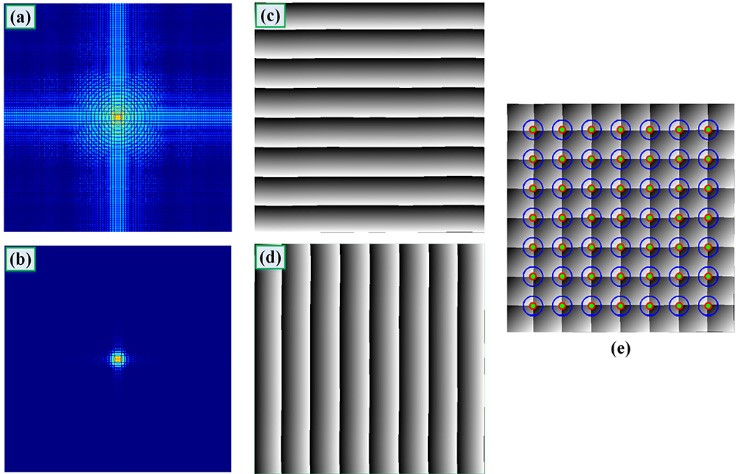
3.2基于傅里叶变换的圆阵列标靶的特征提取 14
3.3模拟分析 17
3.3.1 Matlab仿真平台简介 17
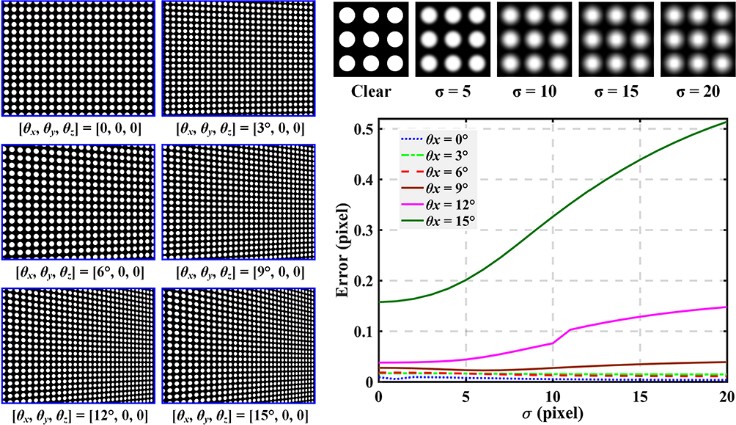
3.3.2特征提取的精度验证 17
3.2.3标定精度验证 19
第四章 实验与结果分析 20
第五章 结论 22
参考文献 23
致谢 25
第一章 绪论
1.1研究背景
在人类的日常生命活动中,视觉系统扮演着最基本最重要的角色。据统计,人类信息活动中大约有80%以上是通过视觉系统来完成的。作为迄今为止,人类所发现的最完整、功能最丰富的视觉系统,人类视觉系统是计算机视觉不断追寻的目标。利用机器来模仿人的视觉,并在某项具体事务中协助甚至代替人的工作,提高生产流程中的效率与精度、降低经济成本和环境成本,是发展计算机视觉的主要目的[1]。随着信息技术的快速发展,20 世纪中期产生了统计模式识别,研究基于以二维图像的方式表达、分析视觉信息,并得到了广泛的应用;之后信息处理能力快速提高,对物体三维信息的识别、测量逐渐成为计算机视觉领域的研究重点。
计算机视觉是一个多学科交叉的新兴领域,且与人工智能的发展紧密联系,包括信号处理,应用数学,地理信息等多领域的学者都加入到对它的研究。其应用在卫星图像处理、生产控制与检测、医学辅助诊断、三维形状分析、机器人智能导航和生物特征鉴别等方面具有重要意义和广泛的应用前景。早期由于卫星照片和航空照片的数量过多,为了辅助对这些图像的解读,产生了许多自动视觉系统,进一步与制导系统结合,实现了精准的末端制导;工业机器人也是计算机视觉应用最广泛的领域,为了更智能地解决机器人的行为规划问题,越来越多的场合要求机器人具有一定的视觉能力,以解决故障规避,特定目标识别等问题;医学上采用视觉技术对医学图像进行分类、判读压缩等工作;几年来,随着移动设备的增加,生物特征鉴别技术快速发展,机器视觉在人脸识别、虹膜识别、屏下指纹等方面也得到了广泛应用[2]。通过各种成像系统与计算机结合像人一样观察并理解世界,是一个长期而艰辛的目标,总之,计算机视觉系统的研究是一个比较新的领域,它与多类学科紧密相关,并且普遍应用于我们的日常生活当中,具有广泛的现实意义和广阔的发展前景 [3]。
精确的相机标定结果是计算机视觉得以广泛应用的基础,标定精度对质量检测、逆向工程、自动化装配和机器人辅助手术等各种应用的性能有很大影响。因此,如何标定,以获得更为准确的相机参数,一直是光学领域的研究热点。
为了确定空间中某点的三维坐标与其在图像传感器上投影坐标的精确对应关系,需要根据成像原理,建立相机的数学模型。相机的数学模型中包含多个参数,主要分为内部参数和外部参数。这些参数描述了相机的特性与它在空间中相对于标靶的位置关系。其中,内部参数主要取决于相机的自身特性,包括焦距、主点和畸变等;外部参数主要与摄像机在空间中的位置与姿态有关,包括旋转矩阵和平移矢量。求解这些参数的过程就是相机标定,一般情况下这些参数需要通过实验与数学运算才能解出[4]。
1.2国内外研究现状
相机参数通常是由三维空间物体表面的某点与其二维图像某点之间的一组精确对应关系来估计的,这些点通常被称为特征点。因此,许多研究都致力于开发具有鲜明特征的标定靶,使得这些特征点能够在标靶图像中被快速、精确地定位和识别。
经过多年的发展,相机标定方法发展出多个种类。根据标靶的维数分类,这些标定方法大致可以分为四类[5]:基于三维物体的标定,基于二维平面的标定,基于一维分段的标定以及OD自标定。基于三维物体的标定通常需要高精度的标定物,由于其结构复杂,性价比不高,目前使用不多,只适用于少数精度要求很高的情形;基于二维平面的标定因其灵活性和易用性成为目前最受欢迎的方法;基于一维分段的标定,要求目标进行一定的约束运动;OD自标定不使用任何标定目标,但需要复杂的数学运算。总的来说,二维平面标定由于其灵活性强,应用范围广泛并且兼顾了标定的准确性,在多数情况下都是首选方法。目前使用最广泛的是张于2000年提出的基于二维平面标靶(一般为棋盘格)的相机标定方法,该方法在空间中任意放置相机与标靶位置,并且利用相机在不同的空间位置与偏转角度下拍摄多张图片,提取特征点坐标后通过数学运算与结果优化即可解出相机参数。
特征点提取是完成摄像机标定至关重要的一步,按照强度分布提取特征点,当图像因离焦而变得模糊后,边界区域难以分辨,不利于特征点的提取。相对于强度分布,采用相位分布的标靶对图像模糊具有较强的鲁棒性。几种动态相位标靶基于以上思想被设计出来,通过多步相移算法计算其截断相位,提取特征点,即使在相机离焦的情况下也可以达到较高的标定精度。Sagawa等在模糊情况下对经典强度分布的标靶与相位标靶进行比较,得出相位标靶在摄像机离焦情况下的特征点提取具有一定优势[6]。Xue等人提出了一种利用同心圆光栅和楔形光栅作为标靶,采用四步相移算法求解零相位交点的摄像机自标定方法[7];Schmalz等人采用横向和竖向分布的相位条纹标靶,利用四步相移算法计算截断相位,并利用格雷灰度编码对截断相位进行解包裹,根据绝对相位分布,提取特征点,该方法最少需要8幅条纹图案[8];Huang等人采用八幅条纹相移标靶完成相机标定,并优化了对相位特征点的提取算法,提高了标定精度[9];Bell等人采用水平和垂直两方向24幅的二值相位标靶进行摄像机标定,提高了在相机离焦下的对比度,提高了相位提取精度[10];Ma等人将相位突变点作为特征点,省去了对截断相位解包裹过程,采用三步相移算法求取截断相位,简化了标定步骤[11]。这些方法在处理离焦图像时可以取得较好的效果,但需要采集多帧图案,换句话说,我们需要在每个相机姿势下捕捉多个图像,这是非常单调繁琐而费力的。
1.3本文的研究内容
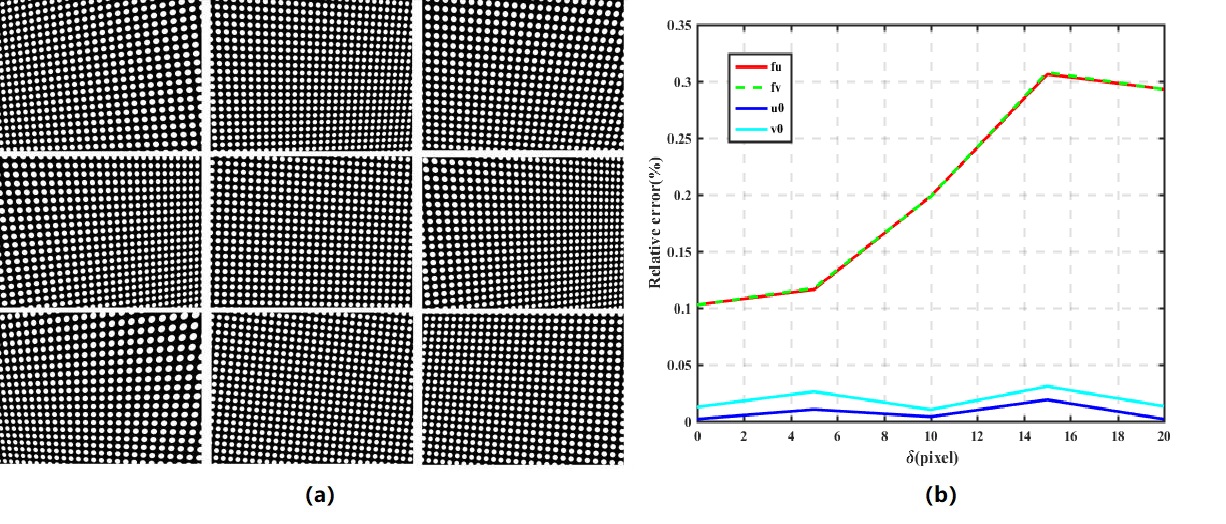
为了克服传统强度分布标靶在离焦状态下难以提取特征点,而相移算法需要在同一视角下采集多张图片,效率不高的缺点,提出了一种基于傅里叶变换的平面二维圆阵列标靶,如图1.1所示。该方法在一个视角下仅需拍摄一幅二维圆阵列图像即可通过傅里叶分析方法和空间相位展开提取特征点。相比于其它方法该方法具有以下优点:
1)二维圆阵列标靶在标定过程中需要采集的标靶图像数量仅为相移条纹标靶的一半;
2)利用傅里叶分析法和空间相位展开法,只需要在每个自由视角下拍摄一张图片而不需要多帧图案,使标定过程更加快速便捷;
- 与传统棋盘格标定相比,采用傅里叶分析法能够较好得抑制高频噪声,提高标定精度。同时对相机的离焦模糊具有较强的鲁棒性,即使在离焦的情况下也可以得到较好的标定结果。
 实验与仿真结果表明,所提方法可以实现快速、高精度标定。
实验与仿真结果表明,所提方法可以实现快速、高精度标定。
图1.1 (a)传统的棋盘格标定靶(b)二维相移光栅条纹标定靶(c)本文所提出的平面二维圆阵列标靶
第二章 理论背景
2.1相机模型
相机参数通常是由三维空间物体表面的某点与其二维图像某点之间的一组精确对应关系来估计的,为了求解这些参数,必须根据摄像机成像原理,建立相机的几何模型。
2.1.1线性模型
 通常在不考虑镜头畸变的情况下,相机模型是一个线性模型,即物点通过透镜的光心投影在图像平面一点上,且不发生歪曲,三者共线[12]。该模型规定了4个常用的坐标系,各坐标系的关系如图2.1所示:世界坐标系是空间中的一个三维直角坐标系,用于描述相机和标靶的空间位置关系,其位置可以根据实际情况而自由确定。相机坐标系的坐标原点是摄像机的镜头光心OC,它也是一个三维直角坐标系,和轴分别与像平面横竖两边平行,轴垂直于像平面且与镜头光轴重合。图像坐标系是一个二维的平面坐标系,它的原点是轴与像平面的交点,横竖坐标分别平行于图像传感器的长边与短边,单位为毫米。像素坐标系与图像坐标系共面,也是一个二维平面坐标系,它的横轴数轴与图像坐标系的平行,且方向相同,区别在于它的原点坐标一般位于左上角而不是中心,由于图像传感器的物理特性,其坐标值一般用整数表示,单位为像素。
通常在不考虑镜头畸变的情况下,相机模型是一个线性模型,即物点通过透镜的光心投影在图像平面一点上,且不发生歪曲,三者共线[12]。该模型规定了4个常用的坐标系,各坐标系的关系如图2.1所示:世界坐标系是空间中的一个三维直角坐标系,用于描述相机和标靶的空间位置关系,其位置可以根据实际情况而自由确定。相机坐标系的坐标原点是摄像机的镜头光心OC,它也是一个三维直角坐标系,和轴分别与像平面横竖两边平行,轴垂直于像平面且与镜头光轴重合。图像坐标系是一个二维的平面坐标系,它的原点是轴与像平面的交点,横竖坐标分别平行于图像传感器的长边与短边,单位为毫米。像素坐标系与图像坐标系共面,也是一个二维平面坐标系,它的横轴数轴与图像坐标系的平行,且方向相同,区别在于它的原点坐标一般位于左上角而不是中心,由于图像传感器的物理特性,其坐标值一般用整数表示,单位为像素。
图2.1 各坐标系位置关系示意
物体在图像传感器上的成像过程,可以看成各坐标系坐标之间的刚体转换与透射投影过程,要想从世界坐标系转换至离散的像素坐标系,需要引入一系列矩阵。首先可以用一个齐次矩阵来数学描述某点从世界坐标系转换到相机坐标系的过程,这个矩阵由一个平移矢量和旋转矩阵组合而成。设空间中某物点P的三维世界坐标,转换到相机坐标系下的坐标,则P与Pc的转换关系可以表示为:
 (2.1)
(2.1)
其中R表示旋转矩阵,可以看出它是一个单位正交矩阵,它的参数值取决于摄像机在空间中的朝向,如果沿X, Y, Z轴旋转的角度分别为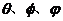 ,那么旋转矩阵就可以表示为(2.2);而t表示平移向量,它的值取决于两坐标系的位置关系也就是摄像机相对于标靶在空间中的位置。
,那么旋转矩阵就可以表示为(2.2);而t表示平移向量,它的值取决于两坐标系的位置关系也就是摄像机相对于标靶在空间中的位置。
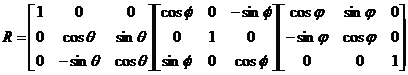 (2.2)
(2.2)
从相机坐标系向图像坐标系的转换是一个从三维到二维的投影过程,两坐标系之间的映射关系可以表示为:
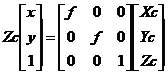 (2.3)
(2.3)
其中f表示摄像机的焦距。而从图像坐标系向像素坐标系的转变,可以看成是数据离散处理的过程。参考图2.1,假设O点在像素坐标系下的坐标为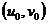 ,单个像素沿x,y方向所占的物理尺寸为:dx、dy,那么图像坐标系中坐标为
,单个像素沿x,y方向所占的物理尺寸为:dx、dy,那么图像坐标系中坐标为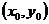 的点转换到像素坐标系后的坐标分别为:
的点转换到像素坐标系后的坐标分别为:
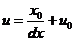
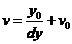 (2.4)
(2.4)
化为齐次坐标表示形式可得:
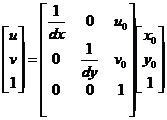 (2.5)
(2.5)
结合(2.3)与(2.5)式,相机坐标系到像素坐标系的的转换关系如(2.6)所示 :
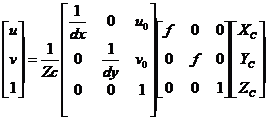 (2.6)
(2.6)
在实际中由于制造工艺的局限性,像素坐标系的u,v轴不一定相互垂直,从而引入一个倾斜因子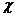 (Skew Factor)。综合上公式(2.5)和 (2.6),并考虑倾斜因子,我们可以得到摄像机的线性数学模型:
(Skew Factor)。综合上公式(2.5)和 (2.6),并考虑倾斜因子,我们可以得到摄像机的线性数学模型:
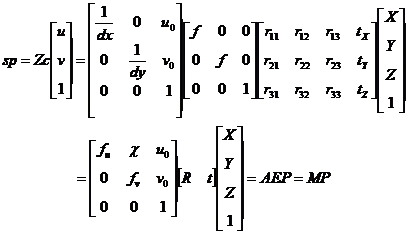 (2.7)
(2.7)
式中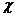 表示倾斜因子;s=ZC表示比例因子(Scale factor); fu和fv分别为u,v方向上的等效焦距; 矩阵A为内参矩阵,它的参数取决于相机自身特性;矩阵E的参数取决于相机在空间中与标定物的位置关系,被称为外参矩阵;M=AE称为投影矩阵,是两矩阵相乘得到的一个齐次矩阵。
表示倾斜因子;s=ZC表示比例因子(Scale factor); fu和fv分别为u,v方向上的等效焦距; 矩阵A为内参矩阵,它的参数取决于相机自身特性;矩阵E的参数取决于相机在空间中与标定物的位置关系,被称为外参矩阵;M=AE称为投影矩阵,是两矩阵相乘得到的一个齐次矩阵。
2.1.2非线性模型
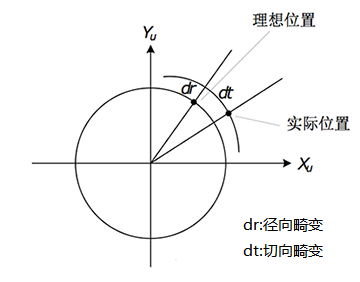 图2.2透镜成像的非线性模型
图2.2透镜成像的非线性模型
畸变是对直线投影的一种偏移。透镜存在多种畸变,最常见的为径向畸变、切向畸变和薄透镜畸变等等,其中以径向畸变与切向畸变对透镜成像效果的影响最大,所以一般情况下我们只考虑径向畸变与切向畸变。如图2.2所示,由于畸变的存在,使得原本线性的模型变为了非线性,上述的摄像机线性数学模型不再适用于描述成像过程,应该引入非线性畸变模型对上述模型加以修正。
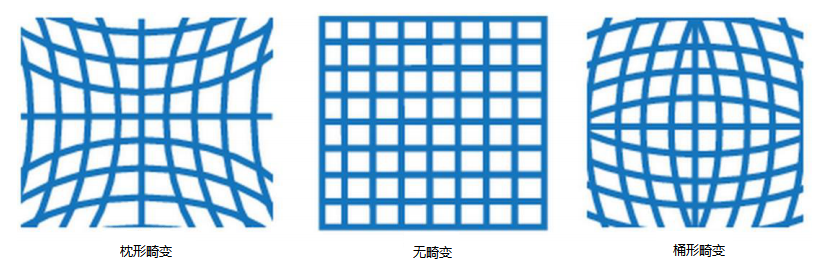 径向畸变是透镜在制造时的工艺误差造成的,使透镜的径向曲率发生不规则变化,径向畸变关于主点对称分布,越接近透镜边缘,畸变越严重。图2.3分别展示了两种常见的径向畸变类型:
径向畸变是透镜在制造时的工艺误差造成的,使透镜的径向曲率发生不规则变化,径向畸变关于主点对称分布,越接近透镜边缘,畸变越严重。图2.3分别展示了两种常见的径向畸变类型:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: