基于大数据的三峡过闸船舶到闸时间优化开题报告
2020-04-12 15:53:30
1. 研究目的与意义(文献综述)
1.1研究背景
水路运输是目前各主要运输方式中兴起最早、历史最长的运输方式。其技术经济特征是载重量大、成本低、投资省,但灵活性小,连续性也差。较适于担负大宗、低值、笨重和各种散装货物的中长距离运输,其中特别是海运,更适于承担各种外贸货物的进出口运输。长江历来被称为黄金水道,它的地位和价值,是任何其他交通运输方式所不能取代的,具有无可比拟的优点。三峡水运已成为连接中部地区和长江三角洲经济区和城市群的重要纽带,但是给水运管理和运营带来了挑战,在三峡水运中如何降低营运成本已成为持续关注的问题,航速优化则是一种减少船舶营运成本,提高经济效益的有效措施。船舶推进功率与航速成3次方关系,因此航速过高会导致油耗增加从而导致运营成本上升,航速过低则会增加航行时间从而导致运营成本上升,同时为保证安全性,在风浪条件下的航速会受到限制,所以需要通过考虑实际情况并使用数学建模来确定一个最佳航速,使船舶在保证安全的条件下,以较快的速度到达港口且营运成本尽可能降低。
1.2国内外研究现状
2. 研究的基本内容与方案
2.1研究整体思路
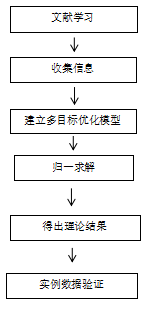
本次研究的整体思路是通过对船舶到闸时间优化的文献学习。在此基础上,收集仿真数据,并通过仿真数据分别根据在不同风浪条件下,船舶营运成本和最小到港时间对航速进行建模分析。通过收集三峡船舶营运成本的信息建立一个关于航速的目标函数,主要考虑租船成本以及燃油成本,航速越高,油耗越高,燃油成本就越高。但航速越低航行时间越长,租船成本也就越高。然后收集关于不同风浪条件下的航速的信息建立一个目标函数,主要是不同海况下保证安全航行的前提下的最大航速。最后再利用Pareto多目标问题优化原理建立多目标优化数学模型得出最优解集。得出在不同风浪条件下以较快的速度到达港口且考虑运营成本航速综合性的理想模型。最后通过与实际数据进行对比验证。
2.2 Pareto多目标优化问题概述
工程问题中往往存在多个目标,这些目标有时会发生冲突,因此需找到最佳解 决方案以同时满足多个目标的要求,这就是多目标优化问题。对于m个目标函数的多 目标优化问题,通常可表述为:

在多目标优化问题中,大多数情况下各个优化目标之间是相互冲突的,某个目标性能的改善可能会导致其他目标性能下降。同时使所有目标都达到最优是不可能实现的,只能在各个目标之间进行折中和权衡,使所有的目标函数尽可能地达到最优。因此,对于多目标优化问题。其最优解不是一个单独的最优解,而是给定约束条件下的Pareto最优解集。
2.3 研究方法
2.3.1文献调查
为完成课题,搜集了大量的文献资料,对目前有关航速优化研究文献进行分析,査阅了有关营运成本和不同风浪下的最大允许航速信息,以及多目标优化问题建立模型求解的方法和理论,了解相关方面的现状,补充了课题相关的研究工具,吸取优秀作品的精华,加强对课题的理解程度。
2.3.2 数据收集与分析
首先收集营运成本信息,从三峡船舶运输的营运成本数据库中进行筛选,尽量选取同类型船舶在同种海况下(不考虑风、浪、流、船体污底等因素的影响)不同航速下的营运成本信息,尽可能剔除其他因素影响,忽视其他次要因素,将航速视为主要因素。然后收集在安全范围内不同风浪条件下船舶航速所允许的范围,尽量选取同类型船舶,不考虑其他因素影响,将风浪条件视为主要制约因素。最后收集三峡船舶在不同风浪条件下的营运成本信息,只考虑最小到港时间和营运成本这两个主要目标(选取的数据在不同风浪条件下,除航速条件外其他条件应尽可能相同)。
2.3.3建立数学模型
首先以营运成本为目标函数,利用所收集的三峡船舶营运成本的信息,建立起一个考虑营运成本的航速优化数学模型,推导航速对营运成本的影响。最小营运成本主要包括燃油成本和租船成本,可建立如下目标函数:

其中F1表示营运成本,C1表示重油成本,C2表示轻油成本,C3表示租船成本,vi,ti,Li表示航段i的航速,航行时间及航行距离,vmin表示最小航速,vmax表示最大航速。
其次利用所收集的不同风浪条件下较为理想的航速允许条件,建立一个考虑风浪条件的航速模型,推导出风浪条件对船舶最小到港时间的影响,最小到港时间如下:
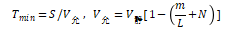
其中Tmin表示最小到港时间,S表示航行距离,V允许表示海上允许航速,V静表示船舶静水中的航速,即设计航速或最大连续速度,L表示船舶垂线间长,相关参数选择可参考下表:
| 蒲氏 风级 | 顶浪 | 斜顶浪 | 横浪 | 斜顺浪 | ||||
| m | N | m | N | m | N | m | N | |
| 5 | 9 | 0.02 | 7 | 0.02 | 3.5 | 0.01 | 1 | 0 |
| 6 | 13 | 0.06 | 10 | 0.05 | 5.0 | 0.03 | 2 | 0.01 |
| 7 | 21 | 0.11 | 14 | 0.08 | 7.0 | 0.05 | 4 | 0.02 |
| 8 | 36 | 0.18 | 23 | 0.12 | 10.0 | 0.07 | 7 | 0.03 |
2.3.4实验证明
将收集到的三峡船舶在不同风浪条件下的以较快航速运行时的营运成本数据带入数学模型中,在不考虑其他因素的条件下,将其与所得最优解进行对比,观察差异大小,从而验证数学模型的合理性与可靠性,最后得出结论。
3. 研究计划与安排
3.进度安排
| 周次 | 工作内容 |
| 1∽3 | 完成文献阅读和开题报告 |
| 4∽6 | 收集信息 |
| 7∽10 | 建立分别关于营运成本和不同风浪下最小到港时间的模型 |
| 10∽12 | 将得到的两个模型进行归一得到多目标优化模型并求解集 |
| 13∽14 | 完成论文初稿 |
| 15∽16 | 论文修改准备答辩 |
4.指导教师意见
指导教师签名:
4. 参考文献(12篇以上)
5.参考文献
[1] 陈吉荣, 王雁飞. 船舶过坝优化调度辅助决策系统在长江三峡通航管理中应用[j]. 水运工程, 2001(10):70-74.
[2] 杨宝璋,石爱国.大风浪中多因素优化航向航速选择[j].中国航海,1991(01):30-40.




