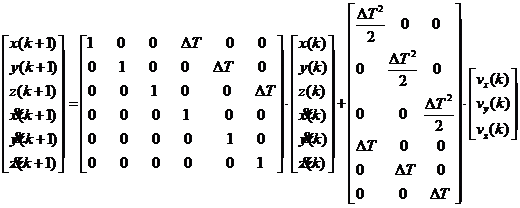基于Cubature卡尔曼滤波的水下机器人目标跟踪算法毕业论文
2020-04-05 11:00:48
摘 要
随着海洋经济的发展和我国的海洋强国战略的实施,水下机器人的研究越来越成为一个全球热点,水下机器人不仅能带来商业价值还能广泛应用于军事领域,是一个未来的前沿技术领域。作为水下机器人的核心技术目标跟踪技术无疑是重中之重。如何能最大限度的去除误差得到精确的目标数据又是目标跟踪技术中的核心,而本文研究的就是基于容积卡尔曼滤波的水下机器人目标跟踪技术,容积卡尔曼滤波算法在近几年中广泛应用于精确目标估计中,在工程中展现出了精度高、稳定性好、实现简单等优越性能。因此本文通过数学建模的方法模拟水下机器人的运动,然后通过比较卡尔曼滤波、拓展卡尔曼滤波和容积卡尔曼滤波对其运动误差的处理结果,判断容积卡尔曼滤波的优劣,最终得到如下结论:
1)本文得出容积式卡尔曼滤波算法在复杂水下环境下对于误差的处理效果优于拓展卡尔曼滤波。
2)在非线性系统内的经典卡尔曼滤波对于误差的处理结果非常糟糕,但在线性系统内对于误差的滤波处理结果优异,再次印证了经典卡尔费曼滤波只适应于线性系统。
3)在较小的误差环境中(即非线性程度较低)容积卡尔曼滤波和拓展卡尔曼滤波表现的差异并不是跟大,但是在较大的误差环境中容积卡尔曼滤波对于误差处理的结果要优于拓展卡尔曼滤波。
4)拓展卡尔曼滤波和容积卡尔曼滤波的收敛速度要快,另外容积卡尔曼滤波的数值稳定性和跟踪精度要更高。
关键词:容积卡尔曼滤波;卡尔曼滤波;拓展卡尔曼滤波;非线性;水下机器人
Abstract
With the development of marine economy and the implementation of China's ocean power strategy, research on underwater robots has increasingly become a global hotspot. Underwater robots can not only bring commercial value but also can be widely used in the military field, and are a future frontier Technical field. As the core technology target tracking technology of underwater robots is undoubtedly the most important thing.
The way to remove the error to get the accurate target data is the core of the target tracking technology. This article will study the underwater robot target tracking technology based on the Cubature Kalman Filter, and the Cubature Kalman Filter algorithm in recent years. It is widely used in accurate target estimation and exhibits superior performance in engineering such as high accuracy, good stability, and simple implementation.
Therefore, the mathematical modeling method is used to simulate the motion of the underwater robot. Then by comparing the Kalman Filter, Extended Kalman Filter and the Cubature Kalman Filter, the processing result of the motion error is used to judge the merits of the Cubature Kalman Filter. The following conclusions:
1) This paper concludes that the Cubature Kalman Filter algorithm is superior to the Extended Kalman Filter in the processing of errors in complex underwater environments.
2) Classical Kalman Filtering in nonlinear systems is very bad for error processing, but the Filtering results for error in linear systems are excellent, again confirming that classical Kalman Filter is only suitable for linear systems.
3) In a smaller error environment (a lower degree of non-linearity), the difference between the performances of the Cubature Kalman Filter and the Extended Kalman Filter is not large.But in the larger error environment, the Cubature Kalman Filter is better than Extended Kalman Filter.
4) The convergence speeds of the Extended Kalman Filter and the Cubature Kalman Filter are faster. In addition, the numerical stability and the tracking accuracy of the Cubature Kalman Filter are higher.
Key words: Cubature Kalman Filter; Kalman Filter; Extended Kalman Filter; nonlinear
目录
摘要 I
Abstract II
第1章 绪论 1
1.1 研究背景 1
1.2 国内外研究现状 1
1.3 滤波研究概述 3
1.4 本文主要研究内容和技术路线 4
第2章 卡尔曼滤波算法 6
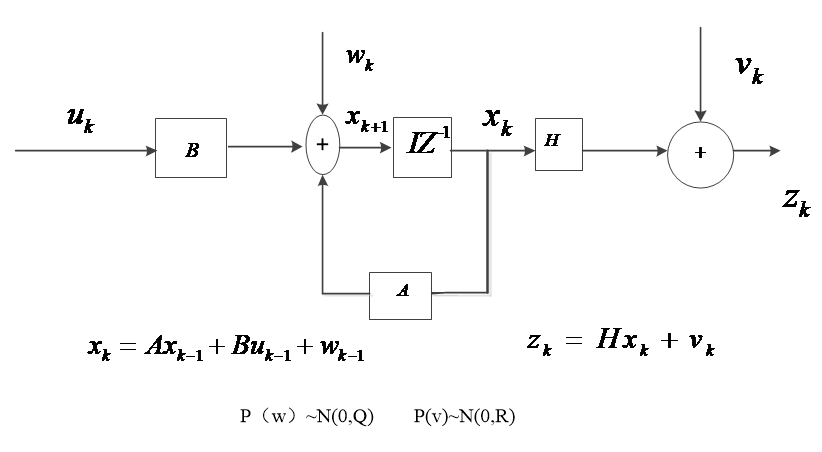
2.1卡尔曼滤波 6
2.1.1 卡尔曼滤波介绍 6
2.1.2 数学名词介绍 6
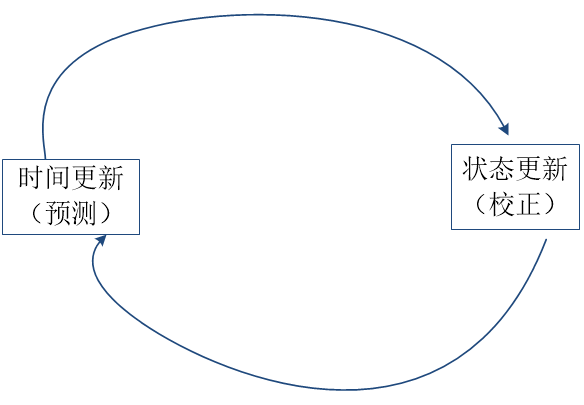
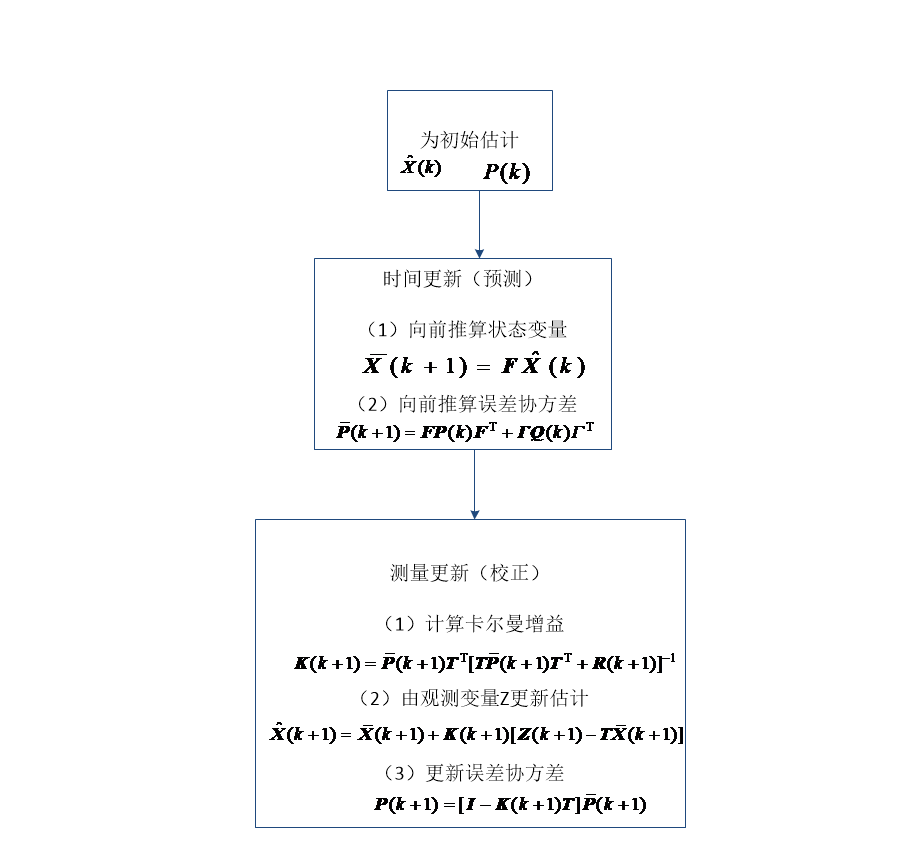
2.1.3 滤波流程 7
2.2 模型讲解 8
2.2.1 流程图 8
2.2.2 迭代示意图 9
2.3目标跟踪Kalman滤波 10
2.3.1系统模型 10
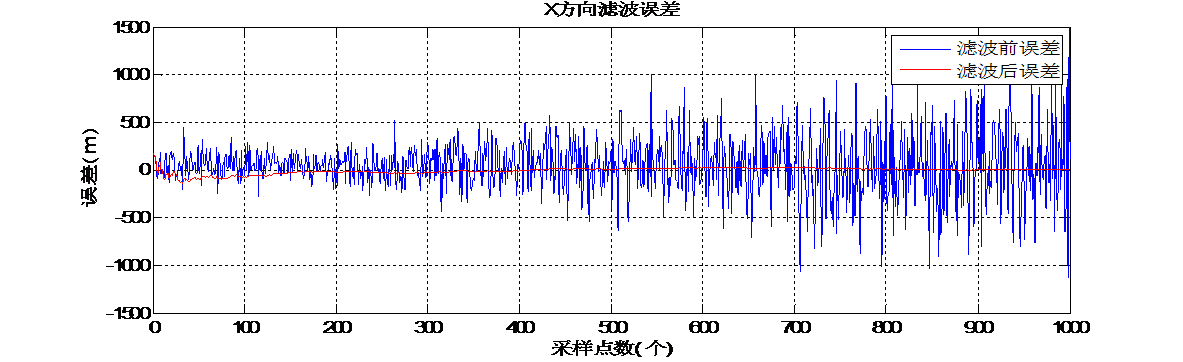
2.3.2 误差对比 13
2.4 本章小结 15
第3章 拓展卡尔曼滤波 16
3.1 拓展卡尔曼滤(EKF)波介绍 16
3.1.1 拓展卡尔曼滤波算法基本理论 16
3.2 EKF与KF对误差处理的比较 18
3.3 拓展卡尔曼滤波的不足 19
3.4 本章小结 19
第4章 Cubature卡尔曼滤波 20
4.1 Cubature卡尔曼滤波介绍 20
4.2 容积卡尔曼滤波算法原理 20
4.2.1 Cubature卡尔曼滤波 20
4.3 CKF算法流程 23
4.4本章小结 24
第5章 算法仿真 25
5.1 本文的仿真条件设定 25
5.1.1 运动方程 25
5.1.2 量测方程 26
5.2 仿真值设定 26
5.3 误差对比 27
5.4 本章小结 28
第6章 总结与展望 29
6.1 总结 29
6.2 展望 30
参考文献 31
致谢 33
附录 34
第1章 绪论
1.1 研究背景
世界海洋覆盖地球表面的三分之二,对整个历史中的人类福祉至关重要。就像在古代一样,他们使国家之间的货物运输成为可能。在近期,我们看到海上采矿业的出现以及天然气水合物的开采。同样,海洋也可能通过飓风和海啸等自然现象威胁人类安全并破坏基础设施[1]。我国是海洋资源大国,但并不是强国,我辈肩负着中华民族伟大复兴的重任,目前海洋开发正在如火如荼。最前沿的莫过于水下机器人技术,水下机器人技术在军事领域,渔业,海底探测等方面正在扮演着越来越重要的角色。其中目标跟踪是水下机器人稳定工作的关键技术之一,目标跟踪就如同水下机器人的眼睛和耳朵,因此,进行水下机器人的目标跟踪研究具有明显的重要意义和工程价值。目前无人水下航行器(unmanned underwater vehicle ,UUV)的目标跟踪主要是指UUV检测目标的有效辐射(例如声辐射和电磁辐射),以获取目标相对于UUV的连续方位角[2]。但是有一个问题是,在水下恶劣情况下被动声呐的测量精度很低,且海洋情况复杂,例如海水温度、密度和盐度变化,噪声统计特性(平均值和协方差)未知,估计的准确性未知。非线性的测量量存在于UUV的目标跟踪中,给滤波算法带来了极大的困难,因此精算滤波算法对于UUV的目标跟踪来说具有极大的工程意义[3-5]。
1.2 国内外研究现状
20世纪40年代左右,美国专家维纳(Wiener)和前苏联科学家科尔曼过洛夫(Kolmogorov)都先后研究出维纳滤波理论。维纳研究维纳滤波的初衷是解决火炮控制问题的,但由于此事关系国家军事机密,直到1949年美国科学家维纳才对外公布维纳滤波原理。因为维纳滤波使用的是频域计划法,于是只能处置安稳的随机进程。维纳滤波的思想是操纵谱分化和平稳随机进程的谱展开式来办理最优滤波的题目的。在频域当中设计维纳滤波器,就必然面临维纳-霍普方程的求解,该方程特点之一就是计算量大,同时也需要大量的储存空间。正是由于维纳滤波原理的这些天然劣势妨碍了它在实际系统中发挥作用,也就意味着维纳滤波器在物理层面上是永远不可能实现的。如果我们想在物理层面上得到维纳滤波器,就必须将传递函数的部分分式展开,但遗憾的是维纳滤波是非递推的,而且它的历史数据需要全部储存。正是由于以上种种的天然劣势使得维纳滤波器迟迟不能在工程上发挥作用。
20世纪60年代初期,随着技术的发展和革新,尤其是电子信息技术和高速计算机技术的腾飞,人们对优越滤波器的渴望越来越急切。在这种时代背景下,卡尔曼滤波器应运而生。它冲破了经典维纳滤波器种种局限,创造性地提出了时域的状态空间方法,并且创造了系统的状态空间和状态变量的观点。状态空间的突出特征是:用状态方程表示动态系统,用量测方程显示状态系统的观测信息,把系统中的状态抽象为一个“点”,再利用希尔伯特(Hilbert)在空间中的射影定理来处理最优状态估计的问题,像这种状态空间方法我们称之为卡尔曼(Kalman)滤波方法,用这种方法建立的状态估计理论我们称它为卡尔曼滤波理论。卡尔曼滤波算法是一种立足于计算机上的,并且易于实时实现的最优滤波算法,由于其数据的存储量小,使得卡尔曼滤波可以从容地处理平稳的随机过程和非平稳过程,这就是得卡尔曼滤波成功的突破了经典维纳滤波算法的窘境。也正因如此卡尔曼滤波在机器人、制导、跟踪、石油地震探测、故障诊断等方面大显神威。但是随着时代的发展和计算机技术的进步,卡尔曼滤波对数值的稳定性、实时性、有效性和计算效率的处理结果已经越来越不能满足人们的需求了。并且由于计算机字长有限的原因,导致了在计算机计算的过程中产生了误差和截断误差积累、传递,最终致使误差方差矩阵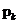 的对称正定性消失,造成了数值的不稳定等严重后果,以上诸问题严重的困扰着无数的工程科研人员。在漫长的科技发展道路上,无数科研人员废寝忘食,苦思冥想的创新卡尔曼滤波,以求改善卡尔曼滤波对于数值处理的稳定性和提高计算效率。研究人员分别提出过平方根滤波、奇异值分解滤波以及UD分解滤波等方法[17]。
的对称正定性消失,造成了数值的不稳定等严重后果,以上诸问题严重的困扰着无数的工程科研人员。在漫长的科技发展道路上,无数科研人员废寝忘食,苦思冥想的创新卡尔曼滤波,以求改善卡尔曼滤波对于数值处理的稳定性和提高计算效率。研究人员分别提出过平方根滤波、奇异值分解滤波以及UD分解滤波等方法[17]。
自从卡尔曼滤波理论问世以来,无数的科研人员都致力于将其应用于非线性估计问题。20世纪90年代前期,对于解决卡尔曼滤波的数值稳定性问题,科研人员尝试用分解、补偿算法的方式解决。到了20世纪90年代后期,非线性理论进步神速 ,科研人员摒弃了以往的泰勒(Taylor)展开式近似的方法转而采用了计算更加简便,精度更好的插值多项式近似的方法,对非线性变换的方法对非线性的模型来变换,走出来传统的线性变换思想[18]。插值法起源于挪威学者Schei,1995年,挪威科学家Schei创造性地提出来用中心差分的方法来改进卡尔曼滤波。也是在同年,牛津大学教授Julier、Uhlmann等人创造性地推出Unscented滤波。随后,来自美国的专家Vander Merwe、Wan等人将Uscented滤波理论进行了创新。这也使得Uscented滤波可以经由一种非线性变换-U变换完成了对误差协方差和非线性状态模型的更新。随着计算机技术的革新和发展,以卡尔曼滤波为基础的现在估计理论已经在航空航天、大地测量、图像处理、故障诊断、控制工程、信息融合等领域作为核心技术在使用[19 -22]。
对于非线性系统状态的精确估计是绝大多数工程领域所面对的难题[6][7]。目标跟踪方法主要包括扩展卡尔曼滤波器(EKF),最小二乘估计(LSE),Unscented卡尔曼滤波器(UKF),粒子滤波(Particle Filter,PE)。
目前,应用最广的非线性系统状态估计方法是拓展卡尔曼滤波器(extended Kalman Filter,EKF)[8],传统EKF的原理是非线性系统通过一阶泰勒级数展开式的方式来转化为线性问题,但EKF对于高非线性系统的准确性较差。同时EKF需要计算雅可比矩阵,这将导致计算系统的复杂[8]。当非线性函数在通过伪线性变换时,LSE将产生一个有偏差的估计。当UUV执行目标跟踪时,有偏估计对测量的准确性有很大影响。无迹卡尔曼滤波器(Unscented kalman Filter,UKF)通过无迹变换对非线性系统的状态均值和方差进行近似,用构造一组确定的加权样本点的方法来对将要的估计参数进行逼近。这种方法也避免了对非线性对象的线性化建模以及雅可比矩阵的计算,是一种直接应用于非线性系统的状态估计的滤波算法。UKF通过一组确定的加权采样点来逼近随机变量的分布函数,避免了求微分问题[7][8]。但UKF在高维系统中准确度低,计算复杂在工程中很难实现[7]。粒子滤波方法依据蒙特卡洛仿真思想,通过随机产生大量粒子来近似后验概率密度。因此粒子滤波计算量相当大,对于实时性的要求很难满足,且有粒子退化和贫化等问题[8][9]。近期,Arasaratnam等提出了基于Cubature变换的Cubature Kalman Filter(CKF) 具有编号稳定,计算复杂度低,操作简单等优点[10]。该滤波方法一经提出就受到了热烈响应。广大专家学者将其广泛应用于姿态估计、导航、连续系统和混合滤波等领域。CKF滤波过程和UKF大致相同,但其理论推导更加严密细致(UKF缺乏严格的数学推导)。CKF使用Cubature准则,以2n个同等权重值的Cubature点经非线性系统方程转化后产生新的点来给出下一个时刻系统的预测值,同样也不需要对非线性模型线性化。相比较于EKF算法,CKF具备UKF的优点,由于其使用更少的采样点,预计正在不久将取代UKF成为常用滤波方法[12]。
1.3 滤波研究概述
滤波的意义就是从混合在一起的多种信号中得到有用的信号。滤波的前提是必须对系统信号进行测量,然后依照一定的估计准则和特定的统计方法对目标进行估计。滤波的最终意义就是为了优化,我们称之为的“优化”就是在很多的滤波算法中选取最优的滤波算法。“优化”的思想不仅在现实生活中具有非常重要的意义,而且在工程研究中也大有可为。优化思想也将始终贯穿在本文始终,滤波的终极意义也是要得到我们最想要的滤波效果。
滤波一词的出现最早可以追溯到1795年,当时法国的数学家高斯(Carl K.Gauss)为了研究行星运动的轨迹,创造性地提出来最小二乘估计算法,轰动一时[23]。该算法在工程实践应用中不关心观测信号的统计特性,只满足了测量误差的方差最小。所以在大部分情况下该滤波方法性能较差。但是最小二乘法还是凭借其算法简单、原理简单、收敛性能好的优势至今活跃在众多工程领域内。
滤波的应用及其广泛,不管是在导航定位、弹道目标跟踪还是在卫星姿态估计、图像处理、信号处理都是绝对意义上的核心技术。由是观之,滤波技术有我们的生活发展和科学技术休戚相关。
滤波的研究自始至终都是曲折坎坷的,因为自然界本就是线性和非线性的统一体。线性系统是简单的,是我们对世界的最初的认识,但自然界还有一种更为复杂的非线性系统,该系统更加广泛的存在于自然界中,成为了万事万物的变化之本。所以我们要清晰的认识到非线性系统才是世界的本质,只有抓住了这个基本点,我们的研究才能有的放矢,才能目标明确。人类在几千年的研究历程中都是从简单事物到复杂事物的,所以研究滤波也是,我们需要从简单的线性系统到复杂的非线性系统。
滤波的分类,按照滤波所在系统的差异,科学界将其分为线性系统和非线性系统。
其中在线性系统中名气最响的莫过于卡尔曼滤波。在非线性系统中,又可以细分成如下三类:基于函数近似滤波、基于确定性采样滤波、基于随机采样滤波。其中基于函数近似滤波最具有代表性的是拓展卡尔曼滤波;基于确定性采样滤波的代表是无迹卡尔曼滤波;基于随机采样滤波的典型代表是粒子滤波和容积式卡尔曼滤波。
为方便理解,具体如下图:
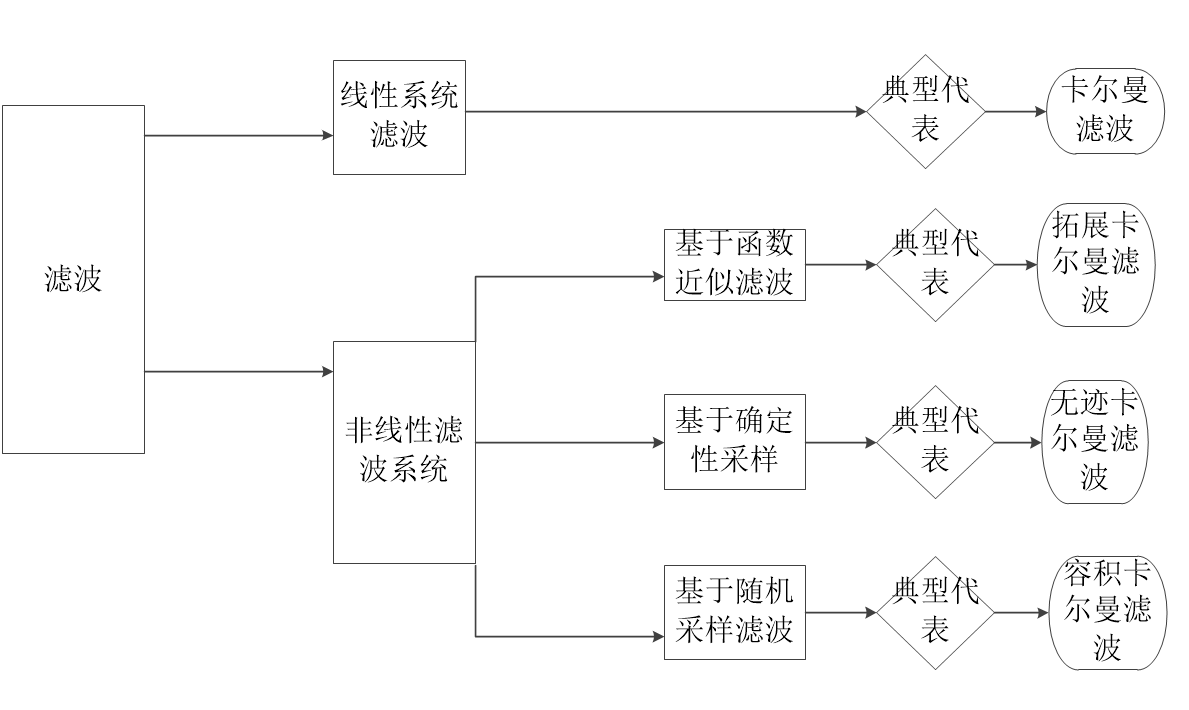
图1.1滤波分类
1.4 本文主要研究内容和技术路线
本文主要研究内容是基于水下机器人的容积卡尔曼滤波算法,鉴于Cubature卡尔曼滤波算法的众多优势可以在工程上带来重大意义,本文就是要通过建立数学模型的方法模拟水下机器人在水下的运动产生一系列运动姿态和运动数据,并且在加大噪声的恶劣情况下比较于传统的卡尔曼滤波方法、拓展卡尔曼滤波方法来验证Cubature卡尔曼滤波算法的优越性。具体是:
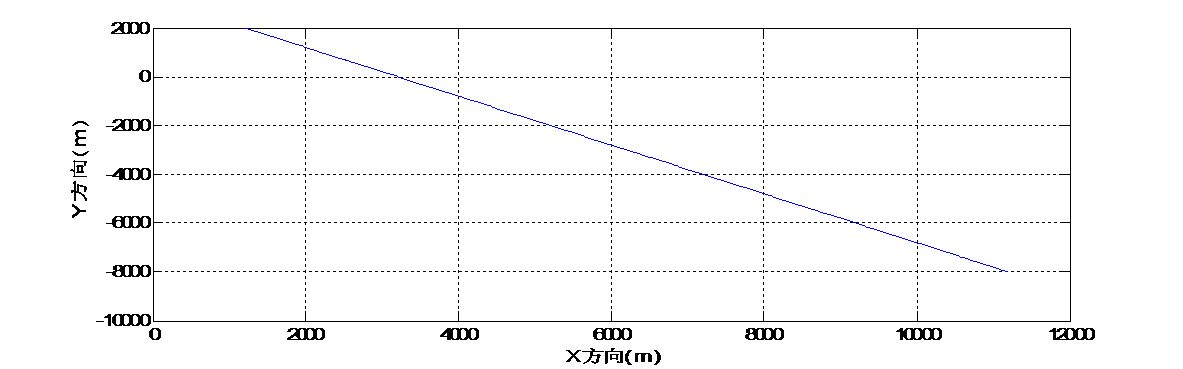
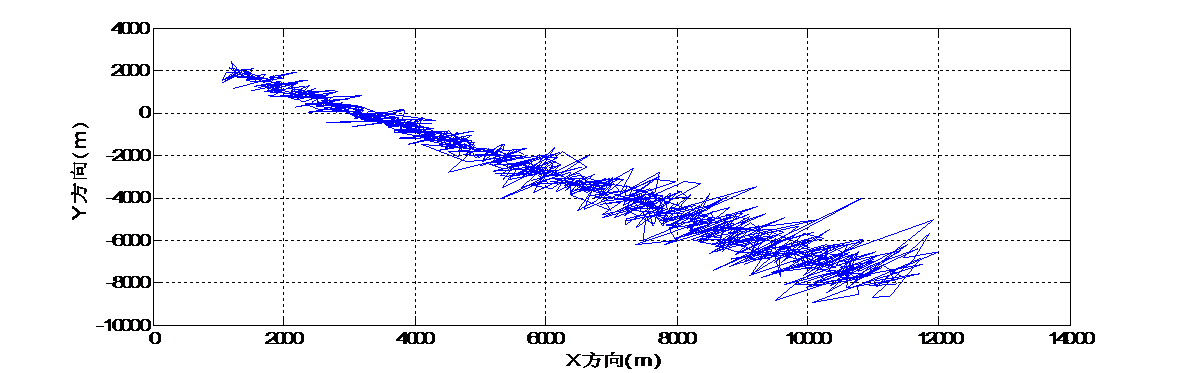
1)通过建立数学模型的方法产生直角坐标系下的坐标位置和数据,再通过坐标系的转换产生球坐标系下的坐标位置和数据,在转换的过程模拟产生噪声误差以模拟真实情况,至此完成模拟声呐信号采集,产生了声呐信号数据。通过在MATLAB中画图的方式画出水下机器人在水下运动的真是轨迹和测量轨迹,通过两幅图的对比,直观的反映出减小测量误差,提高测量精度对工程应用的重要性。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: