基于ANSYS的轴-旋转壳耦合特性分析毕业论文
2020-02-19 09:08:55
摘 要
本文所研究的对象是轴-旋转壳系统,本文介绍了国内外研究现状、有限元分析法,通过ANSYS分析软件建立了轴-旋转壳耦合系统的有限元模型。为其设置边界条件以出计算其自由振动特性(即系统的固有频率、固有振型)和强迫振动特性(系统在艉部激励下的振动特性)。接着讨论了横向振动、纵向振动的耦合特性。
本文第一章在查阅学习学者的研究成果上,介绍了水下航行器振动研究的背景意义和国内外研究现状。为进行轴-旋转壳耦合特性分析打下一些基础。
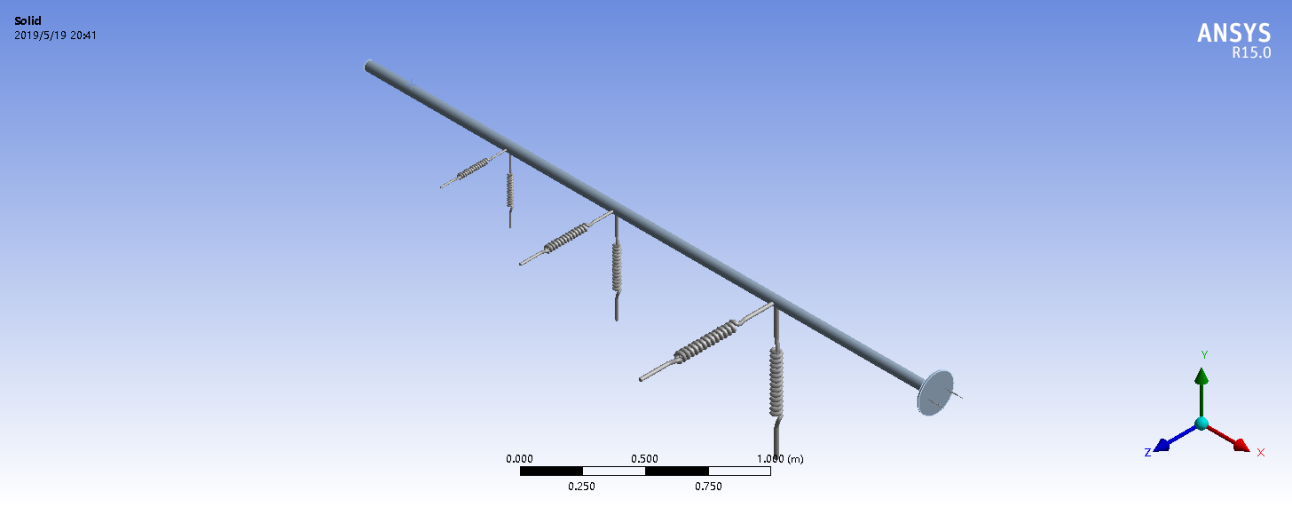
第二章简单介绍了ANSYS Workbench软件,并详细介绍了轴-旋转壳系统的建模,模型壳选择的是圆锥 圆柱壳,轴使用梁单元简化,轴承基座用弹簧简化。然后详细介绍了模型的建成与简化以及模型的具体尺寸。为在下一章节中对该模型进行模态分析以及谐响应分析做好基础。
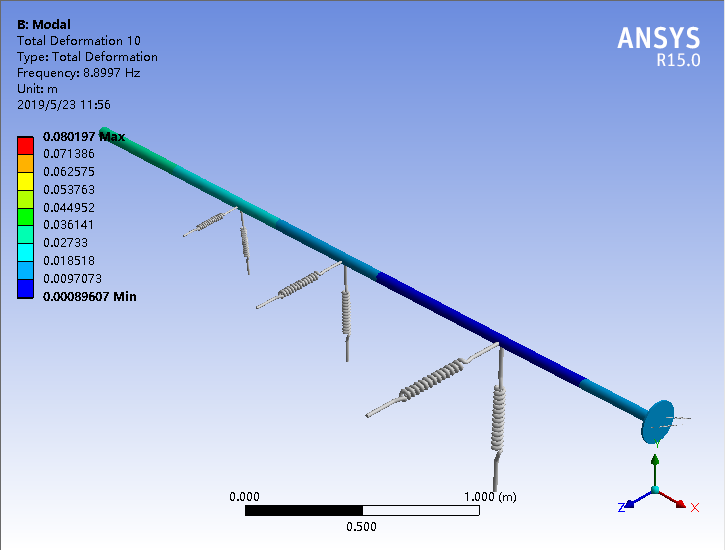
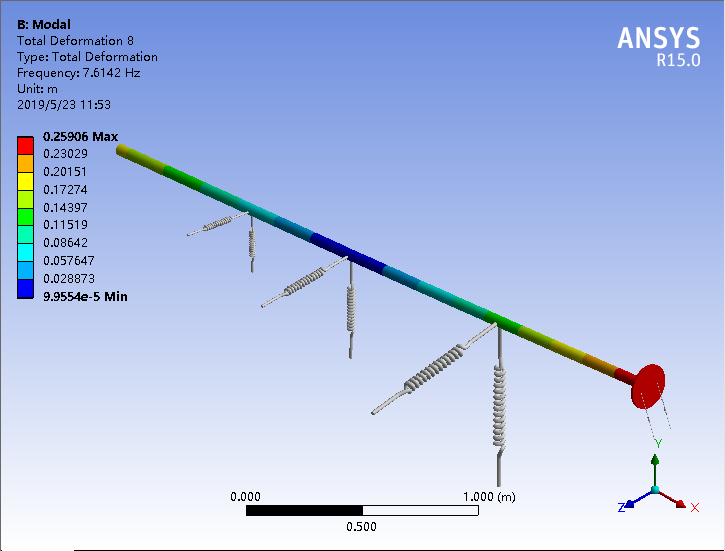
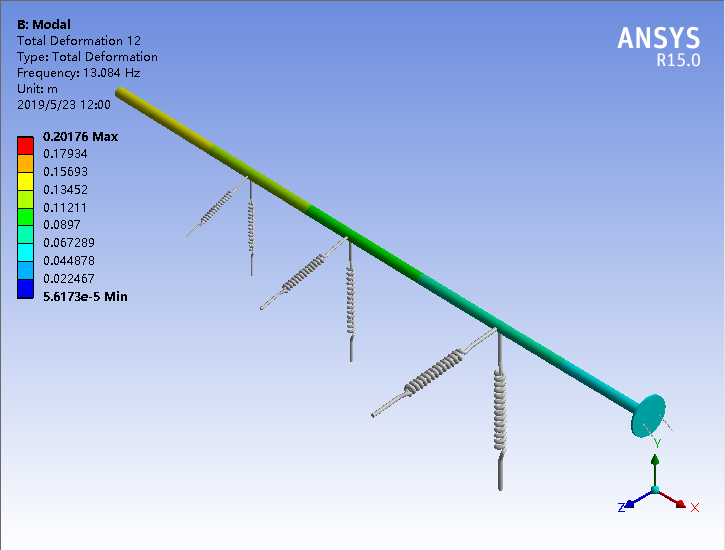
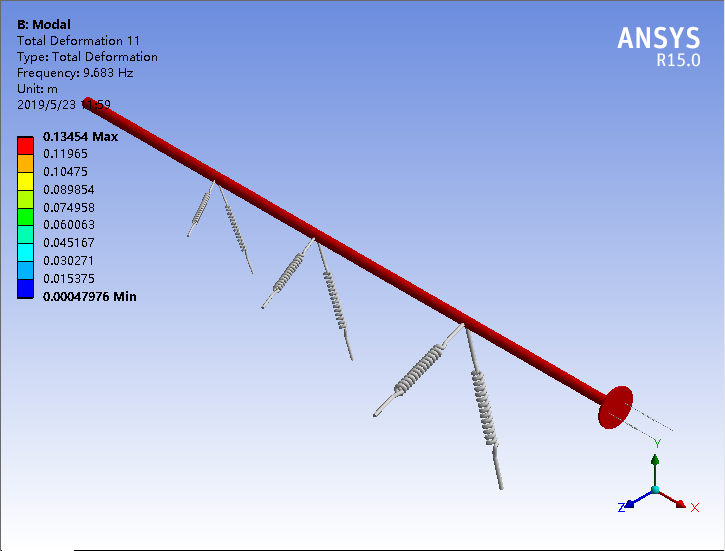
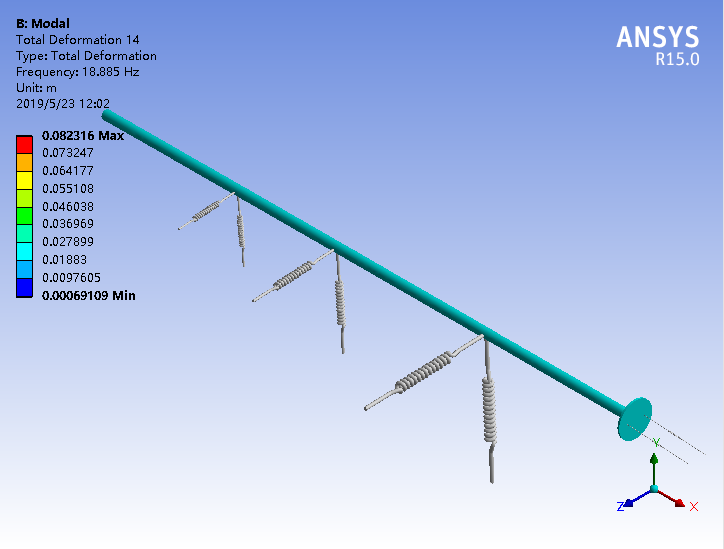
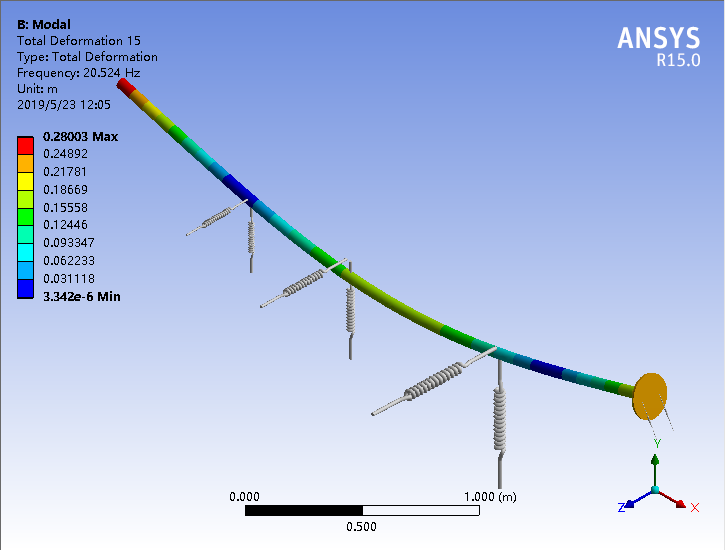
第三章开始对模型进行了模态分析,在无约束的条件下,选取得到17个模态振型。然后进入基于模态分析结果的谐响应分析,为了分析不同激励、相同激励下轴壳不同方向不同观测点的振动耦合特性。设置了轴的横向激励、轴的纵向激励、壳的横向激励、壳的纵向激励四个工况。将计算得到的数据处理后导入Origin软件得到分析图。通过讨论分析得以下结论。
- 在轴、壳的纵向激励下,系统出现了横向位移响应,在轴、壳横向激励下,系统出现了纵向位移响应,出现了耦合纵横振动效应。
- 不同激励下比较,激励在轴上时,轴的横向位移响应和纵向位移响应大于壳上的;激励在壳上时,壳的横向位移响应和纵向位移响应大于轴上的。
- 同一激励时不同观测点比较,在纵向激励下,轴壳不同观测点的横向位移响应和纵向位移响应情况无明显区别;在横向激励下,壳体远离激励源端的观测点位移响应强于近激励源端的观测点,而轴体在观察纵向位移响应时近强远弱,横向位移响应没有明显区别。
关键词:耦合振动;ANSYS;轴-壳耦合系统;有限元法;
Abstract
The object studied in this paper is the shaft-rotating shell system. This paper introduces the research status at home and abroad and the finite element analysis method. The finite element model of the shaft-rotating shell coupling system is established by ANSYS analysis software. The boundary conditions are set for it to calculate its free vibration characteristics (ie, the natural frequency of the system and the natural mode) and the forced vibration characteristics (the vibration characteristics of the system under the excitation of the ankle). Next, the coupling characteristics of lateral vibration and longitudinal vibration are discussed.
In the first chapter of this paper, the background significance of the research on the vibration of the underwater vehicle and the research status at home and abroad are introduced. To lay the foundation for the analysis of the coupling characteristics of the shaft-rotation shell.
The second chapter briefly introduces the ANSYS Workbench software, and introduces the modeling of the shaft-rotating shell system in detail. The model shell is tapered cylindrical shell, the shaft is simplified by beam unit, and the bearing base is simplified by spring. Then the construction and simplification of the model and the specific dimensions of the model are introduced in detail. This is the basis for modal analysis and harmonic response analysis of the model in the next section.
In the third chapter, the modal analysis of the model is started. Under the condition of no constraint, 17 modal modes are selected. Then, the harmonic response analysis based on the modal analysis results is entered, in order to analyze the vibration coupling characteristics of different observation points in different directions of the shaft and shell under different excitations and the same excitation. The four conditions of the lateral excitation of the shaft, the longitudinal excitation of the shaft, the lateral excitation of the shell, and the longitudinal excitation of the shell are set. The calculated data is processed and imported into the Origin software to obtain an analysis chart. The following conclusions were analyzed through discussion.
(1) Under the longitudinal excitation of the shaft and the shell, the lateral displacement response appears in the system. Under the lateral excitation of the shaft and the shell, the longitudinal displacement response appears in the system, and the coupling longitudinal and horizontal vibration effects appear.
(2) Compared with different excitations, when the excitation is on the shaft, the lateral displacement response and longitudinal displacement response of the shaft are larger than that on the shell; when excited on the shell, the lateral displacement response and longitudinal displacement response of the shell are greater than those on the shaft.
(3) Compared with different observation points at the same excitation, there is no significant difference between the lateral displacement response and the longitudinal displacement response of different observation points of the axial shell under longitudinal excitation; under lateral excitation, the displacement response of the casing away from the excitation source is strong. At the observation point near the excitation source end, the axial body is nearly strong and weak when observing the longitudinal displacement response, and the lateral displacement response is not significantly different.
KeyWords:Coupled vibration;ANSYS; Shaft-shell coupling system; Finite element method;
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 研究背景及意义 1
1.2国内外研究现状 1
1.3结构振动的研究方法简介 3
1.3.1解析法 3
1.3.2 有限元法 3
1.3.3 边界元法 3
1.3.4 统计能量法 4
1.3 研究的基本内容 4
第2章 轴-旋转壳系统耦合特性分析理论和建模 5
2.1有限元法分析介绍 5
2.2 ANSYS Workbench简介 6
2.3轴-旋转壳系统建模 7
2.4本章小结 9
第三章 轴-旋转壳的模态分析及谐相应分析 10
3.1 模态分析 10
3.1.1模态分析简介 10
3.1.2模态分析结果 10
3.2 谐响应分析 14
3.2.1谐响应分析简介 14
3.2.2不同激励下系统受迫振动分析 15
3.2.3同一激励下系统受迫振动分析 17
3.3 本章小结 19
第四章 总结 20
4.1 主要工作和结论 20
4.2 研究展望 20
参考文献 21
致 谢 22
第1章 绪论
1.1 研究背景及意义
潜艇是现今重要的战略性武器之一,他依靠其高隐蔽性和突然性,能在水层的掩护下隐藏行迹并发动突然袭击,这是水面舰艇所不可及的。潜艇第一次出现在人类战争舞台是在1910年前后,在二战上,潜艇发挥了超强的战斗力。二战后,世界各国海军高度重视新型潜艇的研发。随着核能和战略导弹装备, 潜艇的发展进入了一个新的阶段。近年来, 中国实力不断增强, 海上战略逐渐受到关注, 潜艇已成为国防事业极其重要的力量。但与此同时, 潜艇技术的发展促进了各种反潜技术应于武器、侦察系统作战平台登军事领域,这得益于近年来潜艇技术的飞速发展,一个全面的潜艇作战系统逐渐在水下、空中、道路、太空登等领域形成。这将对潜艇的生存和运行构成巨大威胁。因此, 提高潜艇的隐蔽性具有十分重要的意义。
潜艇辐射噪声谱包括两部分:连续谱和离散谱。因为不同潜艇的散射声谱组合是独一无二的, 利用声纳系统捕获到潜艇的散射声谱后,敌军可以通过分析散射光谱的组合可以知道潜艇型号, 这样会降低潜艇隐蔽性,也大大增加了潜艇在作战中的安全隐患。可以对离散频谱的低、中频造成很大影响的,是螺旋桨、轴和发动机的速度。螺旋桨振动流向壳体的主要原因是螺旋桨轴,因此研究潜艇轴-旋转壳系统耦合特性具有十分重要的意义[1]。
轴系是整个水下动力装置的主要部分,也是重要部分。它包括轴承、联轴器、传动轴等多个部件,在轴系运行过程中, 主机的励磁、轴系自重量的弯曲变形、螺旋桨的阻力和扭转以及轴振动的推力效应是不可避免的。轴系振动受各种因素的影响。如果轴系和主机的振动达到一定程度, 动力的传递效率就会降低, 甚至主体也会振动。由于船体的振动影响船舶航行性能和航行安全, 研究船舶推进轴的振动特性具有十分重要的意义[2]。
1.2国内外研究现状
船舶发动机和螺旋桨之间是通过潜艇轴系来能量传递。同时, 船舶获得有轴系方向船舶过来的螺旋的推力,使得船舶向前运动。潜艇推进轴系的主要部件包括螺旋桨、中间轴、推力轴、油润滑主轴承、水润滑橡胶轴承、法兰、联轴器等。
驱动轴系的螺纹和横向振动可能是由于主机的传动扭矩不均匀、设备位置偏差、材料不均匀、加工方法不准确和质量偏差等原因引起的。流场的旋转产生不均匀的推力和交替的弯矩, 构成了船舶艉部的紊乱源, 可能导致船体整体和局部等振动。螺旋桨的推进力, 船舶的推进轴变形, 可能会引起横向和纵向振动以及这些振动的耦合。归纳总结起来,所有的振动产生的原因是,第一,船载设备的运行;第二,设备运转时内部出现不平衡和力的变化产生影响[3]。
基于船舶上的轴系振动方面,Jame A[4]通过给螺旋桨施加轴向激励,测试了被厚钢板堵闭两端的薄圆柱壳的振动特性;贾晓军[5]等提出了基于遗传算法轴弯曲振动的固有频率。Korczewski[6]提出了一个简化模型,该模型允许根据在支撑件之间的思维跨度点处测量的轴偏转幅度来估计所产生的扭转振动的总能量。国内研究人员同样做出了许多研究。张勇[7,8]建立了研究轴系弯曲耦合振动的数学模型,它是基于分段连续质量模型的。陈之炎[9]吧回旋振动的原理在其文献中做了一定深度阐述,通过数学推导得到了比较实用的判据判断回旋振,还研究了船舶推进轴系时回旋振动的特点。王小立[10]在文献中研究了轴系纵-扭耦合、弯-扭耦合中,改变轴系径向刚度对系统造成的影响。徐翔[11]研究得到了圆截面梁的扭转-轴向耦合的振动位移方程,分析了轴-壳振动耦合固有频率的变化趋势;总结了在其轴-壳耦合振动研究中发现的尚存的待改进点。然后通过三种振动形式下,两两耦合振动方程的推导,导出了圆截面梁的轴向-横向-扭转耦合振动方程;周春良[2]对船舶轴系振动做了较系统的研究,他利用三维建模软件建立了比较真实的船舶轴系的三维实体模型,通过ANSYS,改变参数,详细分析出了船舶轴系固有模态特性的影响原因,并计算分析了轴系在不同激励作用下的频率振动响应,最后得出结论对船舶轴系振动影响很大的是螺旋桨激励。唐艾飞[12]用MATLAB软件开发了集轴系扭转振动、纵向振动和回旋振动计算于一体的轴系振动计算软件,并通过实例验证了软件的正确性。杨成春[13]既研究轴、壳单个系统对整体的影响,也关注二者耦合系统的对激励的响应特性,所以它在建立了三个系统,包括单独的轴系子系统、壳体子系统。何在空气和水下两个环境下的轴系-壳体耦合系统有限元模型,分析了三种模型模态,以及纵向、横向激励下轴壳系统的耦合振动特性,并通过对比研究的处理不同模型在激励下的振动响应规律。李攀硕[14]等也通过子系统结构建模,分析出轴-壳耦合系统在各种激励下的系统振动特性,明确了系统振动特性受到轴承材料等参数的影响。还比较了轴上螺旋桨激励与控制力的轴壳机械振动情况。
圆柱-圆锥壳振动方面,邓乃旗[17]提出了水下环肋圆锥壳在低频、典型和弹性边界条件下的自由振动与受迫振动声辐射的解析方法, 研究了水下环肋圆锥壳低频时的声振特性。陈美霞[18]等研究了低频下浸没式加筋锥壳的振动特性和远场声辐射。通过完全耦合有限元/边界元模型的数值结果验证了分析模型的结果。
1.3结构振动的研究方法简介
1.3.1解析法
解析法的思想是在数学上通过建立对应的模型将结构振动工程中结构振动所研究的实际问题转换成数学物理方面的问题,首先写出系统运动方程然后通过运算算出其运动的方法,这就是最先所使用的运用在结构振动问题上方法。它的优点是定义清晰易懂、容易把系统进行分开和再组合、能将繁杂的问题分开分析、易于揭示影响系统振动过程中的振动特性的因素等优势,所以解析法一直被国内外学者的所青睐。但解析法缺陷在于,在复杂模型的情况下其推掉十分繁琐,更甚着不能建立推导,在现实工程问题中也常常不能得出解析式;对于模型欠合理的简化处理也会造成一些重要影响因素被忽略;另外一些为创建解析式而设的假设往往存在不合理的情况;包括但不限于以上的原因使得解析法在兼容性和正确性上会被一定程度上的限制。
在解决系统振动的研究上,被经常使用的具体方法有傅里叶级数展开法、模态叠加法、变分法等。模型的简化方法上,经常运用到最简单规则的结构单元如杆、梁、板、柱壳以及球壳等进行组合再推导。
1.3.2 有限元法
在所有方法中,利用数学数值运算方法解决工程问题被公认效果最好的方法就是有限元法。
有限元法求需要给定边界约束和最初条件。在有限元运算分析时,第一步将结构划分为有限个单元,也就是进行离散处理,然后再给每个单元建立它们的刚度矩阵和质量矩阵,每个单元形函数只和形状和坐标系的选取有关。但是在结构振动的情形,位移场应与各阶的模态和振型有关系
相对于其他方法,有限元有许多独特的优点,第一,有限元分析法普遍适用于个各种模型结构;第二,不同物理问题它都能适用,如流体问题、弹塑性问题、屈曲问题、热导问题等,通用性很高;第三,现代计算机技术的高度发展,使得有限元分析的实现更加容易。比较常用的有限元分析软件包括ANSYS、NASTRAN等。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: