摘 要

单元制造在制造企业中得到了广泛的应用，而在市场需求快速变化的背景下，跨单元制造的现象难以避免。为了快速响应市场需求，共享企业制造资源，本文研究了网络环境下运输能力受限的具有柔性路径的跨单元调度优化问题。

首先，为了减少当前运输策略中车辆的空载行程，提出了一种在制造单元之间共享车辆来运输特殊工件的新运输策略，并提出了以最小化总成本和最大完工时间为目标的跨单元调度模型。

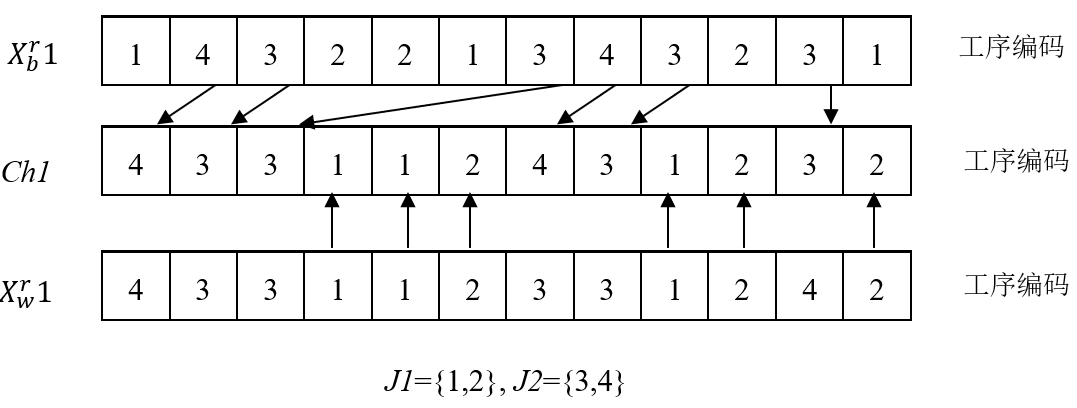
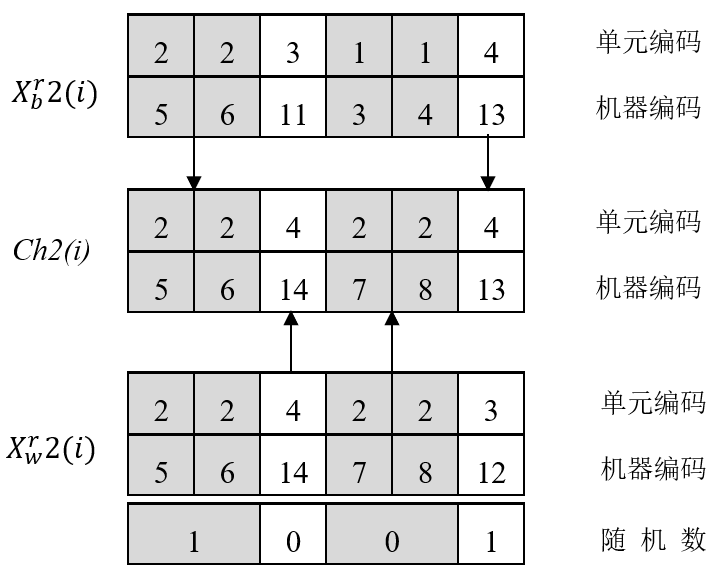
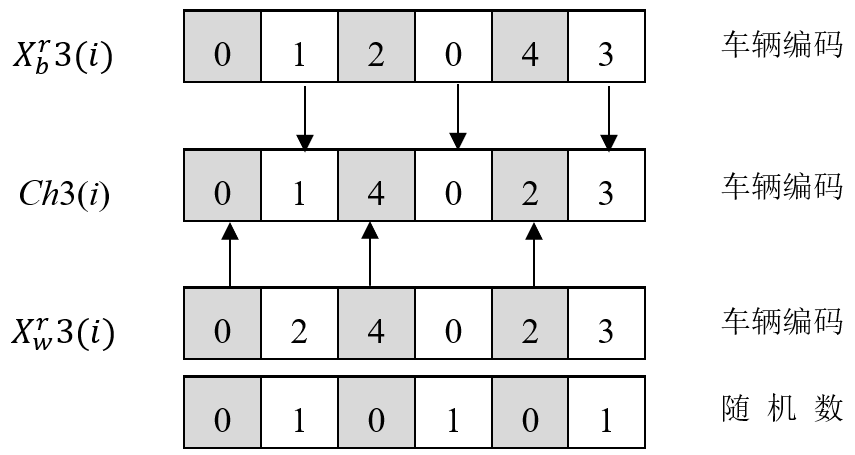
然后，采用了一种四段式编码方式对工件加工顺序、加工工件的制造单元、跨单元加工的机械设备以及运输车辆的分配进行编码，并设计了一种用于求解所提出模型的混合蛙跳算法（SFLA）。在此基础上设计了运输能力受限下具有柔性路径的跨单元调度优化软件。

最后，针对同一实例，将采用新运输策略的优化结果与采用当前运输策略的优化结果进行比较，明显发现所提出的新运输策略可以在总成本和最大完工时间上产生更优解。由于两种运输策略产生的优化调度方案和车辆路径都不同，为了展示两种运输策略的差异，比较了在同一工件调度方案下两种运输策略的优化结果。结果表明，所提出的运输策略可以减少车辆的空载行程，从而减少最大完工时间和总成本，证明了本研究的有效性。

关键词：单元制造；跨单元调度；运输能力受限；柔性路径；混合蛙跳算法；

Abstract

Cellular manufacturing has been widely used in manufacturing enterprises, but with the market demands rapidly changing, the inter-cell manufacturing is inevitable. In order to quick respond to the market demands and share manufacturing resources among enterprises, a inter-cell scheduling optimization problem with flexible routes and limited transportation capacity in the network environment is studied.

Firstly, in order to reduce the unloaded routes of vehicles for the current transportation strategy, a new transportation strategy of sharing vehicles to transport exceptional parts among the manufacturing cells is proposed. And a inter-cell scheduling model is proposed to minimize the total costs and the makespan.

Then, a four-segment coding method is adopted to code the processing sequence of parts, the cells for machining parts, the machines for inter-cell processing and the transportation vehicle allocations. And a Shuffled Frog Leaping Algorithm (SFLA) is designed to solve the proposed model. On this basis, a scheduling optimization software for inter-cell scheduling problems with flexible routes and limited transportation capacity is designed.

Finally, the optimization results of the new transportation strategy and the current transportation strategy for the same instance are compared. It is obvious that the proposed transportation strategy could yield a better solution on both total costs and makespan than the current transportation strategy. As the optimized scheduling scheme and routes of vehicles yielded from the two transportation strategies are all different, to show the differences of the two transportation strategies, optimization results of the two transportation strategies are compared under a same parts scheduling scheme. The results show that the proposed transportation strategy can reduce the unloaded routes of vehicles, thus reducing the makespan and total costs. Validates of the study is verified.

Key words: Cellular manufacturing; Inter-cell scheduling; Limited transportation capacity; Flexible routes; Shuffled Frog Leaping Algorithm;

目录

第1章 绪论 1

1.1研究背景与目的 1

1.2国内外研究现状 1

1.3论文结构 3

1.4本章小结 3

第2章 运输能力受限下具有柔性路径的跨单元调度优化模型 4

2.1问题描述与假设条件 4

2.2新运输策略 4

2.3符号说明 5

2.4目标函数与约束条件 6

2.5本章小结 7

第3章 运输能力受限下具有柔性路径的跨单元调度优化算法 8

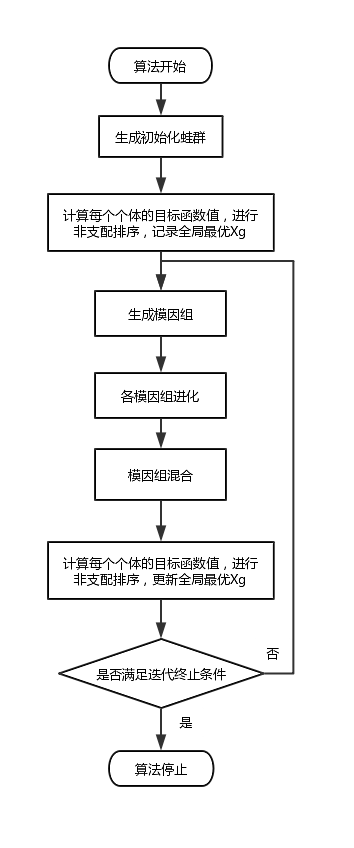
3.1混合蛙跳算法 8

3.2编码与解码方式 9

3.3模因组的生成 10

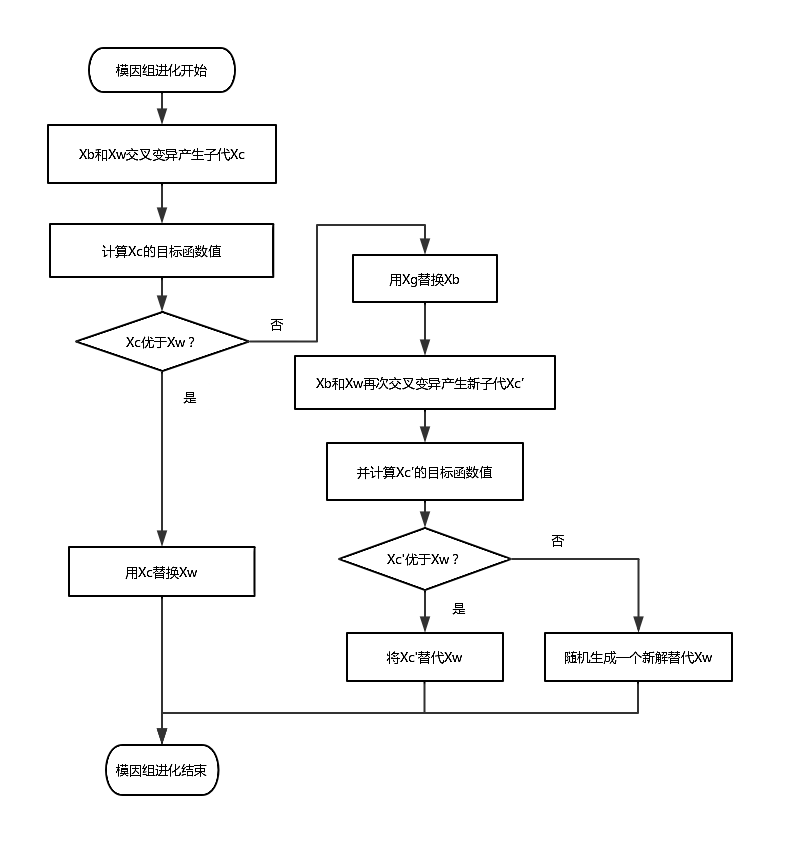
3.4交叉和变异 10

3.4.1交叉 10

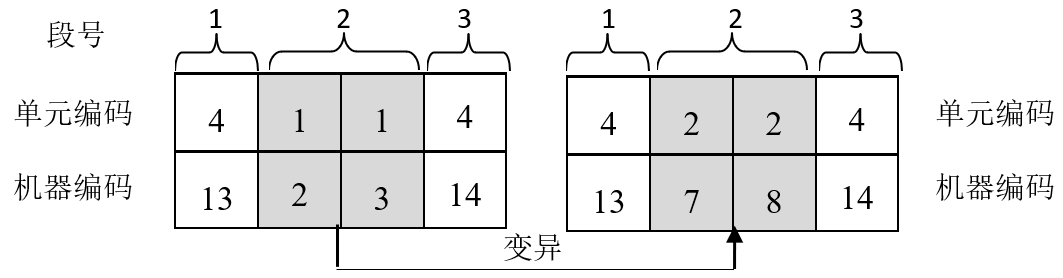
3.4.2变异 12

3.5算法步骤 13

3.6本章小结 14

第4章 运输能力受限下具有柔性路径的跨单元调度优化软件设计 15

4.1跨单元调度优化软件总体设计 15

4.1.1软件功能需求分析 15

4.1.2软件模块化设计 15

4.2用户界面设计 16

4.2.1主界面设计 16

4.2.2数表生成界面设计 17

4.2.3计算求解界面设计 20

4.3用户界面的实现 22

4.3.1主界面的实现 22

4.3.2数表生成界面的实现 23

4.3.3计算求解界面的实现 24

4.3本章小结 25

第5章 仿真实验与结果分析 26

5.1不同运输策略下的调度对比 27

5.1.1新运输策略 27

5.1.2当前运输策略 30

5.1.3相同工件调度下两种运输策略的对比 32

5.2不同车辆数量对调度的影响 34

5.3本章小结 35

第6章 总结与展望 36

6.1总结 36

6.2展望 36

致谢 37

参考文献 38

第1章 绪论

1.1研究背景与目的

单元制造系统（Cellular manufacturing systems，CMS）是成组技术的一项应用，根据成组技术将工件分为不同的工件族并用相应的机械设备来加工工件，提高了生产制造的柔性，能够快速响应市场对多品种小批量的需求。单元制造有诸如缩短准备时间、减少在制品库存、易于运作控制等等多种优点^[1]。

理想情况下的单元制造，每个工件都能在一个单元内完成其所有工序的加工。随着社会需求向多样化发展，产品快速更新，一些新工件的加工无法仅在一个制造单元中完成。而由于企业的生产空间和经费的有限，不能够购买多的新设备。为了快速响应客户需求并节省设备投资，工件无法在一个单元内完成加工的工序可以运输至其他制造单元完成加工，跨单元制造由此产生。需要在两个或多个单元中的机器上进行加工的工件称为特殊工件，特殊工件的跨单元加工工序称为异常工序^[2]。有研究表明，72.9%的大规模工厂采用了单元制造，然而在实际生产中，只有10%的零部件完全没有跨单元制造^[3]。而网络环境下的跨单元制造能够通过单元重构减少制造成本和时间消耗，有利于企业在不购进新设备或重建制造单元的情况下快速的加工新产品。因此，为了快速响应市场变化，降低制造成本，研究跨单元调度问题是很有意义的。

1.2国内外研究现状

单元制造调度和流水车间调度相似，每个制造单元之间没有联系。Schaller以最小化总误工为目标研究了存在族准备时间的单机调度问题^[4]。Logendran等研究了准备时间与排序有关的双机成组调度问题，以最小化总完工时间为优化目标^[5]。Li等以总误工和平均总流水时间最小化为目标解决了族准备时间与排序相关的流水单元调度问题^[6]。这些研究还只是针对单元制造。

以下的研究考虑了跨单元制造问题。Yang等人假设单元制造系统由两个单元组成，每个工件在每一个单元中加工不多于一道工序^[7]。然而，单元制造系统通常包含多个制造单元，并且每个工件可以在单元中加工多道工序。Solimanpur等人将最大完工时间作为优化目标来优化跨单元调度问题^[8]。他们假设在目标单元完成最初分配给它们的所有工件的加工之前，不能发生跨单元转移。然而，跨单元转移可能在现实中的任何时间发生。Tavakkoli-Moghaddam等人研究了最小化最大完工时间、单元内移动、延误和与排序相关的准备成本等多目标的跨单元问题^[9]。他们将这些优化目标加权转化为单目标优化问题。王晓晴等人提出了一种以流水时间为优化目标的跨单元调度优化模型^[10]。Tang等人将总加权延误作为优化目标，通过考虑在多个单元中的机器上加工的特殊工件来研究制造系统中的工件调度^[11]。

上述的跨单元调度研究假设特殊工件的异常工序只能在指定的制造单元中的特定的机器上进行加工。然而实际上，由于在网络环境下，不同的制造单元可以具有功能相同的机器，因此不同制造单元中的机器之间存在能力重叠，工件应该具有可供选择的跨单元加工路径，即柔性路径^[12]。Li等人将完工时间、平均延迟和平均跨单元移动数作为优化目标。他们针对的是具有柔性加工路径和特殊工件需要访问位于多个单元中机器的调度问题^[13]。Feng等人以机器的总负载和完工时间为优化目标，研究柔性路径和机器共享的跨单元调度问题^[14]。Tang等人通过柔性路径解决了多单元工件调度问题，并设计了一种基于拍卖的方法来最小化完工时间^[15]。而邹萌邦^[16]以时间和成本为多目标研究了网络环境下的有柔性路径的跨单元调度。

上述所有的跨单元调度研究，没有考虑在单元间运输的特殊工件的特定运输过程。有些文献^{[17] [18]}忽略了跨单元运输时间。有些文献^{[9] [14]}，假设不同制造单元之间的运输时间是固定值。而还有些文献^[16]中的跨单元运输时间是制造单元之间的实际距离除以车辆运输速度，但其假设每当需要跨单元运输工件时，随时存在可用于运输的车辆。然而，在实践中，单元地理位置上通常分散分布并且运输车辆的数量是有限的。当特殊工件需要进行跨单元加工时，可能无法保证随时空闲的车辆可以用来运输，并且可能需要等待运输。异常工件跨单元运输的车辆调度问题通常被称为运输能力受限的跨单元调度问题^[19]。

目前，很少有研究考虑运输能力受限的跨单元调度优化。Zeng等^[19]将完工时间作为优化目标，并首先考虑了运输能力受限的跨单元调度问题。然而，在他们的研究中没有考虑柔性跨单元加工路径，并且他们假设车辆一次最多可以在不同的单元之间运输一个工件。田云娜等人^[20-21]以总加权延误为优化目标，对运输能力受限、具有柔性路径的跨单元调度问题进行优化。在他们的研究中，一辆车可以一次运输多个工件，工件根据运输的优先级被装载到车辆中，并在每个目的制造单元依次卸载。刘兆赫等人^[22]也以总加权延误为优化目标，研究了运输能力受限的跨单元调度。在他们的研究中，所有工件都被假设为特殊工件，并且考虑了特殊工件的柔性路径。车辆可以一次转移多个零件，一旦车辆空闲，采用启发式规则对等待运输的零件进行分组。

在这些文献^[19-22]的运输策略中，尽管车辆一次运输的工件数量不同，但都存在一些限制，即每个制造单元具有固定的运输车辆，并且制造单元中的工件只能由制造单元所具有的车辆运输。也就是说，当车辆将自身单元的特殊工件运输到其他制造单元卸载后，它需要立即返回到原始制造单元，之后再进行下一次跨单元运输。具有这种限制的运输策略在本文中称为当前运输策略。当前运输策略中车辆的空载行程较多，导致了工件等待运输时间增长、运输成本增加和完工时间延长。此外，这些考虑运输能力受限的研究是基于企业内部范围的优化，而没有考虑在网络环境中不同制造企业之间可能存在具有相似加工功能的制造单元。

1.3论文结构

本文共六章，各章节内容如下：

1. 绪论。首先介绍本文的研究背景与目的，总结国内外研究现状，阐明了单元制造、跨单元制造、柔性路径等概念，分析运输能力受限的跨单元调度特点，以及当前运输策略的限制与不足，最后介绍本论文的结构。
2. 运输能力受限下具有柔性路径的跨单元调度优化模型。首先阐述问题描述以及说明模型的假设条件，然后对本文模型所有的各符号意义进行说明，最后建立数学模型，说明目标函数以及约束条件。
3. 运输能力受限下具有柔性路径的跨单元调度优化算法。首先介绍了混合蛙跳算法的概念与特点，然后说明编码与解码方式、模因组生成、交叉与变异操作等内容的细节，最后总结算法步骤。
4. 运输能力受限下具有柔性路径的跨单元调度优化软件设计。首先分析软件的功能需求，设计软件模块，然后介绍了用户界面的设计与实现。
5. 仿真实验与结果分析。首先设计了网络环境中运输能力受限的具有柔性路径的跨单元调度实例，然后对比分析不同运输策略下的求解结果。最后，对实例问题利用不同数量的车辆进行运输，对比分析新策略下不同车辆数量运输的求解结果。
6. 总结与展望。总结全文，对未来研究进行展望。

1.4本章小结

本章对本毕业设计研究背景以及研究现状进行了详细的说明，阐述了跨单元调度优化问题的研究意义与目的，归纳了目前单元制造和跨单元制造的研究成果，说明了当前运输策略中存在的不足，为后续章节做出铺垫。在本章的最后，对本文研究内容与论文结构进行了一定的说明。

第2章 运输能力受限下具有柔性路径的
跨单元调度优化模型

2.1问题描述与假设条件

网络环境下单元制造系统（CMS）包含了C个来自不同企业的制造单元，每个制造单元有一定量的机器，共M个机器。不同的制造单元可以有功能相同的机器，因此具有相似的加工功能。N个工件可以在候选的单元c中进行加工。由于单元制造功能的限制，某些工件i的某些工序无法在同一个单元完成加工，因此需要跨单元加工。由于CMS中存在制造能力相似的单元，跨单元加工路径是可供选择的，即具有柔性，并且这种需要跨单元加工的特殊工件也能够被任何运输车辆q运输到目的制造单元c'。

假设：

1. 所有工件和机器在零时刻被释放；
2. 所有工件的加工路线是已知的；
3. 工件正在被一台机器加工时，不允许中断和抢占；
4. 用车辆对跨单元工件进行运输，每辆车每次只允许在两个单元间运输一个工件；
5. 忽略同单元内的两道工序间的运输时间；
6. 忽略装卸工件的时间；
7. 运输车辆的速度是常数；
8. 仅当车辆是空闲状态时才能够运输工件；
9. 如果相邻两道工序可以在一个单元内完成加工，则必须在一个单元内完成。

2.2新运输策略

为了减少当前运输策略中车辆的空载行程，本文提出了一种在制造单元之间共享车辆来运输特殊工件的新运输策略。在新运输策略中，零时刻运输车辆随机停放在单元制造系统的某个制造单元中。各车辆与各单元间没有固定的从属关系，车辆在进行完一次运输后不必返回到运输前所停放的制造单元。如图2.1，如果特殊工件i需要跨单元运输，用于运输工件i的车辆q则从当前所在的制造单元c1开始，开往工件i所在的制造单元c2，并在制造单元c2装载工件，然后将工件i运输至目的制造单元c3，这称之为一次运输。如果用于运输工件i的车辆q在本次运输开始时恰好在工件i所在的制造单元c2，且处于空闲可供运输状态，那么c1与c2即是同一制造单元，车辆q从制造单元c1到制造单元c2的运输费用和运输时间则为零。如果车辆q在制造单元c3卸载工件后，没有其他运输任务，则该车辆暂时停留在制造单元c3等待运输任务，否则将继续进行下一次运输。后一次运输的c1即前一次运输的c3。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：