超市收费系统的设计与排员毕业论文
2020-02-19 18:32:19
摘 要
本文主要是以实际生活中的现代超市的收费排队系统为研究对象,对其合理性进行了评估并提出了具体的系统优化方案。该研究的意义在于使收费系统的设计更加符合现实需求,在提升商家经营效益的同时也不影响顾客的购物体验,即在超市经营者利益与顾客利益间建立平衡,具有较强的现实指导意义。
文本采用的主要研究方法是建立排队论中的经典M/M/N数学模型并加以应用。即在实地调研中通过观察记录和随机访问的方法得到所需要的原始数据,再把数据带入到数学模型中,利用MATLAB、Excel等软件进行计算,得到当前收费排队系统的评价结果,之后再通过调整开放窗口数量大小并把相应的评价结果进行对比,来综合确定具体的优化方案。
最后所得的计算结果表明,本文研究的超市排队系统存在着人力资源浪费的问题,而通过调整不同时段开放收费窗口数量,可以对这一主要问题进行改善,最后提升该收费排队系统的合理性和经营利益。
关键词:超市收费系统;排队系统;排队论
Abstract
This paper mainly takes the modern supermarket charging queuing system in real life as the research object, evaluates its rationality and puts forward specific system optimization scheme. The significance of this study is to make the design of the charging system more in line with the actual needs, improve the business efficiency without affecting the customer's shopping experience, that is, to establish a balance between the interests of supermarket operators and customers, which has a strong practical guiding significance.
The main research method adopted in this paper is to establish and apply the classical M/M/N mathematical model in queuing theory. That is to say, in the field investigation, we get the original data needed by observing and recording and random access, then bring the data into the mathematical model, use MATLAB, Excel and other software to calculate, get the evaluation results of the current toll queuing system, and then synthetically determine the specific optimization by adjusting the number of open windows and comparing the corresponding evaluation results. Case.
Finally, the calculation results show that the supermarket queuing system studied in this paper has the problem of waste of human resources. By adjusting the number of open toll windows in different periods, this problem can be improved, and finally the rationality and operational benefits of the toll queuing system can be improved.
Key Words:Supermarket Charging System; Queuing System; Queuing Theory
目 录
一、 绪论 1
1.1 选题背景和意义 1
1.2 研究现状 1
1.3 本文研究内容和写作组织 2
二、 系统分析与数学建模 4
2.1 排队论简述 4
2.2 超市收费排队系统的分析 5
2.3 数学建模 5
三、 超市调研方案设计 7
3.1 调研目的、方法与内容 7
3.2 调研表格设计 7
四、 数据收集与分析 9
4.1 顾客到达率计算及泊松分布K-S检验 9
4.2 服务时间与服务率的计算及泊松分布K-S检验 13
4.3 顾客能容忍的最长等待时间计算 15
4.4 排队系统评价指标计算 15
五、 排队系统调整和优化 19
5.1整体优化思路 19
5.2具体的调整方案及其说明 19
5.3发展建议 22
结 论 23
参考文献 23
致 谢 25
- 绪论
- 选题背景和意义
我国零售业在改革开放以来得到了飞速的发展,全国各地都开设起了大大小小、各类形态的超市,但不管是哪一种规模或者形态的超市,超市收费系统的设计与管理对其经营都至关重要。具体来说,在不同时间段下超市收银台开放数目的多少是设计与优化收费排队系统所需要关注的主要问题。这个问题实际上是一个最优化问题,可以把顾客的等待费用和超市设置收银员所花费的费用之和作为目标函数,把顾客可接受最长等待时间以及超市的盈利大于消耗等作为约束函数来实现目标函数的最优化。[1]
因为在一个时间段内,收银台开放数目过多会造成人力物力的资源浪费,但如果开放过少会造成顾客排队队列过长、结账等待时间过长甚至收银员劳动负荷过大等等问题,影响顾客购物的体验和满意程度,进而影响超市的人气、竞争力和长期收益,因此,超市经营管理者或者超市排队论的研究者的主要工作就是精心设计和调整优化排队系统,在服务机构与顾客两方面利益中求得一个平衡。此外,由于排队系统所处的环境不是一成不变的,所以对该系统的优化也不是一次性和永久性的,而应是一个动态的、长期的过程。
- 研究现状
通过知网搜索近年期刊文献等途径可知,目前国内对超市排队系统的研究较为丰富,而且随着社会物质和精神生产水平的提高,紧贴实际的研究热点也在不断增加。一般的方法是以整个排队系统的经济费用为目标函数,得到最优的服务台配置数量。[2]
高静晨等人将传统的人工结账服务方式与自助服务机器结账方式的流程和特点进行了对比,阐明了后者的优势,然后对北京的几所大型超市结账服务过程进行了考察,再运用排队论的方法用Excel等工具对自助服务机器的结账情况进行了模拟,对得出的结果进行了效率、等待时间等方面的研究。[3]王樱红等人以专门的快递超市排队系统为研究对象,对其进行了分析优化,还根据“双十一”“双十二”等实际情况对约束条件进行了调整。[4]李森彪以M/M/1为基本数学模型,选择了现实生活中存在有“快速通道”的超市的排队系统作为研究对象,对其进行了深度分析和优化设计,它的目标函数是顾客的排队等待时长,该文最后证明了基于“快速通道”设计的双排队系统在一定程度上更优于相对传统的单排队系统,并根据实际情况给出了具体的优化后的服务台配置方案。[2]
这些文章常运用排队论对超市服务强度、队列中排队等待的平均顾客数及顾客在超市的平均逗留时间、顾客平均排队等待时间进行了分析, 建立了超市服务台及人员配备的模型.并用实例证明了模型的适用性。[5]但由于生活中的各种超市具体情况各不相同,此类文章不可能具备完全的普适性,比如根据实际的观测记录要求,有的论文在选取时间段的计量单位是选择了一小时,有的则更加细化选择了半小时;有的超市有自身设计的排队时间和长度限制要求,就围绕着这一标准进行实际验证和提出优化方案[1];当选取了校园超市排队系统作为研究和优化对象,就会结合学生的上课、下课和午休等时间安排来分析系统设置的合理性。
在建立和设计数学模型、考察消费者的心理行为等方面文献资料相似度较高。因为一般而言,大多数超市收费系统组成的输入过程、排队规则、服务机构基本一致,加上实际中的日常生活经验,很多论文研究超市的收费系统时都将其认定为典型的M/M/S/∞/∞/FCFS模型。而对顾客到达率、服务率是否服从负指数分布的验证方法也有多种,既可以使用χ2拟合检验,也可以使用计算机软件如SPSS来完成。
对于超市排队系统近年来还有相关论文结合了数据结构、Arena仿真软件等方面知识进行研究。例如王军设计了一种能够实现动态模拟的多链队,该文把链队头结点都放在一个数组里,以此提升多个链队的操作效率。[6]
就搜索“supermarket checkout/queueing system”“queueing theory”“queueing system”等关键词来看,国外期刊文献对此研究也很丰富,同样基于排队论、计算机软件仿真模拟、算法等技术方法来分析和优化排队系统。
比如Xu J模拟和研究了当n(即超市收银台数目)趋于无穷大时的超市情景,还得出“一些客户抽样更多队列的行为对其他客户具有正外部性”的结论,即个人或群体的行为让其他个体或群体受益或者受损。[7] Kadir N为了分析某一特定排队模型的合理性,运用排队理论设计了一个基本的M/M/1模型解释了不同实体对参数变化的反应,并采用M/M/1队列的MATLAB模型对这些变化进行了观测。[8]Xing W基于M/M/1排队模型和顾客购买商品的数量,建立了超市排队系统的仿真模型。比较了两种不同货物数量下的排队系统,一种是单排队系统,另一种是双排队系统。然后,通过对两个排队系统的经济成本和最优出纳数的分析,得出货物的最优数。仿真结果表明,双排队系统进一步缩短了顾客的停留时间,从而降低了超市经营成本,同时还提升了其运营效益。[9] Ke J C提出使用直接搜索算法来优化服务台不稳定的M/M/C有限缓冲排队系统。[10] Chu L也使用了Arena仿真软件对某公园的排队系统进行模拟和优化,提高运作效益并维持顾客满意度。[11]这些研究都具有参考价值和借鉴意义。
1.3 本文研究内容和写作组织
本文通过分析了超市收费排队系统,构建出排队论中相应的经典M/M/N数学模型,并针对武汉市某中型超市进行了实地调查研究,让本次写作具有现实性和实际参考意义,本文对所收集到的数据进行了汇总、统计和分析,利用SPSS、MATLAB等计算机软件得到了排队论的各种评价指标,结合现实情况对现有的排队系统进行了分析和评价,并在此基础上优化了排队系统,提出解决现存问题的方法,最终实现了对超市收费排队效益的提升。
本文第一章为绪论,叙述了超市排队系统的设计与优化的研究背景及研究意义,然后对这个课题下国内外的研究现状进行了概述,紧接着再对全文整体的组织架构进行了说明阐释。
本文第二章为相关理论预备知识的阐述及其在超市经营业务中的实际应用,即围绕排队论特别是超市排队系统的主要内涵、组成要素、结构特点、符号表达和评价指标等方面进行了说明。
本文第三章为对选定超市排队系统进行实地调研前的方案设计,即对整个调研过程进行了充分的说明,包括具体的数据记录的方式等等。
本文第四章为数据收集和分析,即在利用了第三章的设计方案进行了实地调研后,对已收集到的真实数据进行说明,然后利用Excel、SPSS、MATLAB等计算机软件进行进一步的整理、整合、统计和分析,得到数据集,寻找出数据间的关联,得到顾客到达率、排队系统的服务率和评价指标等等内容,然后结合观察到的实际情况等知识,对所选超市排队系统的现有排队方案进行定性和定量的评价。
本文第五章为对该超市排队系统的优化说明,即针对第四章中所发现的排队系统的问题和缺陷进行了调整和改善,内容包括对优化思路的阐述和对具体优化方案与结果的陈述,最后还就排队系统对该超市提出了的发展建议。
- 系统分析与数学建模
2.1 排队论简述
排队论是数学运筹学大类下一门十分重要的应用型学科,它研究的主要是在随机因素的作用之下出现的排队拥挤现象,广泛应用于交通规划、电子通讯、超市结算付款、银行的个人服务等实际生活问题中,对解决这类问题、优化各种排队系统的运行效率和效益起到了非常大的帮助,其实凡是出现了拥挤现象的场景,都可以运用排队论的方法来解决问题,可以说排队论的产生和发展与现实生活的需要是息息相关的,现代社会生活的不断发展和演进也要求了排队论必须紧跟时代的发展方向和特点。
通常来讲,排队论把排队系统分为以下组成部分:输入过程、到达规则、排队规则、服务机构的结构、服务时间和服务规则。其中:[12][13]
- 输入过程一般用于描述顾客,所谓顾客就是排队系统中接收服务的群体,到达时间间隔所满足的分布情况,常用的包括负指数分布、爱尔郎分布和负二项分布等等
- 到达规则的内涵是顾客到达服务台时是单个到达、多个一起到达还是其它形式到达的
- 排队规则就是系统规定的顾客排队原则,常见的有等待制、损失制和混合制,等待制又细分有FCFS(First Come First Serve,也就是先到先服务)、LCFS(后到先服务)、ROS(随即服务)等等模式
- 服务机构结构的分类有单个服务台、有限多个服务台和无限多个服务台
- 服务时间特指服务台服单独一个顾客所需要的时间,根据服务时间呈现出来的分布规则,又可以分为负指数分布、几何分布等等形态
肯德尔用“A/B/C”这三个符号来表征排队系统,A、B、C分别表达顾客到达的间隔时间分布情况、服务台的服务时间分布情况和服务机构中服务台的数量。通常约定,D表示定长分布、M表示指数分布、G表示一般分布等等。例如M/G/1的内涵就是顾客到达的时间间隔服从指数分布,服务时间满足一般分布,而排队系统中的服务台数量为1。后人在原本三个字母的基础之上又新增了两个字母,分别用来表达排队系统的容量与输入源中顾客数量,比如M/G/1/N/N表示的是在原有基础上多出了其他条件,即该系统最多可容纳N个顾客、输入源中最多只可存在N个顾客。当仅有三个字母,一般认为后两项参数取无限大,也就是系统可容纳顾客数量和顾客源的数量都没有限制。
排队系统的主要评价指标的设定是从顾客与服务机构两个利益方面来考虑和设计的,一方面,顾客为了使得自己的排队时间更少,会希望服务机构开放更多的服务台,而服务机构为了节省投资成本和避免造成人力物力资源的浪费,会限制开放服务机台的数量。根据这些考虑,就形成了包括以下内容的排队系统评价指标,但需要注意的是,并不是所有排队系统都会用到一下全部的评价指标。
- 排队队列总长度,它常常是一个随机变量
- 顾客排队等待时间,指的是从顾客到达排队系统到其得到了服务为止的这一段时间;顾客排队逗留时间则是顾客排队等待时间和服务所花费时间的和。
- 忙期和闲期,忙期内涵是指服务机构处于空闲状态时从有顾客抵达一直到全部顾客都离开系统所耗费的这段时间,而对应的闲期内涵是指服务机构从没有顾客到有任意一个顾客到达系统的这段时间。
超市收费排队系统的分析
因为顾客的到达和超市的服务是随机性的,所以超市收费服务系统是一个典型的随机服务系统,该系统具有如下的特征[14]:
收费的服务对象是选购完商品的顾客。客源具有相互独立性,不同时间段到达收银台的时间间隔具有随机性,但认为在同一时间段内相继到达的时间间隔是确定的,即满足负指数分布,形成的顾客流为泊松流。泊松流具有如下特性[15]:无后效性,在任意两个互不重叠的时间间隔内顾客到达数量是相互独立的;平稳性,在[t △t]这段时间内顾客到达的数量只与时间间隔的长度有关,而与起点时间△t无关;普通性,对充分小的△t,在时间区间(t △t)内有2个或 2个以上顾客到达的概率是一高阶无穷小。
顾客到达间隔时间是随机独立的,服从一种特定的概率分布,收银员的服务时间是随机的独立的,同样服从特定的概率分布。
排队系统有固定的收费窗口数量,每个收银台同时工作且相互之间独立。
综上所述,超市排队系统属于典型的M/M/n排队模型,即顾客相继到达排队系统的间隔时间和服务时间都服从负指数分布,而系统内总共设有n个可运行的收费台,并且该排队系统的系统容量和顾客源数量无限制,实行的是FCFS的等待制。
2.3 数学建模
根据上文内容,已知超市收费排队系统模型为M/M/n,因此,可以设该超市总共有n(ngt;0,n为整数)个可开放的服务窗口,每一个窗口都独立工作互不影响,每个窗口的服务时间都服从负指数分布,令平均服务速率为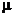 ,就可以得到整个系统的平均服务率n
,就可以得到整个系统的平均服务率n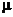 ;
;
在超市收银服务系统中,顾客的平均达到率就是顾客单位时间内达到收银台服务窗口的顾客达到数量[16],设顾客到达强度为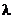 ,有k个开放的收费窗口忙着服务顾客(0
,有k个开放的收费窗口忙着服务顾客(0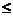 k
k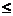 n,k取整数),顾记
n,k取整数),顾记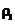 =
=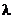 / n
/ n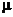 ,
,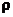 =
=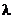 / n,理论上,当
/ n,理论上,当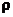 =
=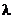 / n
/ n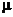 lt;1时,系统存在平稳分布,此时超市服务机构就能正常运作,否则就可能出现排队过于拥堵的现象。
lt;1时,系统存在平稳分布,此时超市服务机构就能正常运作,否则就可能出现排队过于拥堵的现象。
各系统评价指标内涵及其计算公式[12]如下:




