摘 要

基于BESO法的拓扑优化设计平台，是基于双向渐进结构优化算法（BESO算法），结合ANSYS与MATLAB两款软件，能针对设计域复杂、不规则网格的二维、三维情况，实现工程零件的应力最小化设计。

该平台的主要工作流程类似拓扑优化算法中BESO法的执行流程，所不同的是，其中的有限元建模与有限元分析由ANSYS来完成。有限元建模完成后，单元的体积、节点编号、节点坐标、单元刚度矩阵等信息直接传递给MATLAB。每次迭代中模型的有限元求解后，ANSYS将结果参数直接传递给MATLAB，在MATLAB中完成不规则网格下单元的形函数、几何矩阵、应力优化相应的敏感度数值计算，依据不规则单元的应力对设计变量的敏感度高低来增删单元，进行设计变量更新，实现材料的去除和添加，迭代结束后便可得到最终的优化模型。此平台的测试例子包括二维悬臂梁、二维L型梁、三维L型梁，以及三维悬臂梁等的应力优化设计，最终优化结果表明该平台可在目标材料体积的约束下，在设计域内寻找合适的材料分布，完成应力最小化的拓扑优化设计。

该设计平台的开发解决了现有的BESO法在不规则网格下进行应力优化的应用问题，为拓扑优化学术理论与工程实际相结合提供了新的途径。同时，也为拓扑优化方法的研究提供了新的思路，具有一定的借鉴意义。

关键词：BESO法，拓扑优化，不规整单元，ANSYS，应力最小化

Abstract

BESO optimization design platform based on BESO algorithm is based on bidirectional evolutionary structural optimization algorithm (BESO algorithm). Combined with ANSYS and MATLAB, it can realize the stress minimization design of engineering parts for the two-dimensional and three-dimensional situations with complex and irregular grids in the design domain.

The main workflow of the platform is similar to the BESO algorithm in the topology optimization algorithm, except that the finite element modeling and finite element analysis are completed by ANSYS. After the finite element modeling is completed, the volume of the element, node number, node coordinates, element stiffness matrix and other information are directly transmitted to MATLAB. After each iteration solution of finite element model, ANSYS parameter passed directly to the result to MATLAB, completed under irregular grid unit in MATLAB. After that, calculate Geometric matrix, the shape function of optimization, the sensitivity of the corresponding numerical and the stress on the sensitivity of the design variables. According to the stress of the irregular unit level to add or delete unit, to carry on the design variables updated scheme, material can be removed and added. Then, we can get the final end of the iteration of the optimization model. The test examples of this platform include the stress optimization design of two-dimensional cantilever beam, two-dimensional l-shaped beam, three-dimensional l-shaped beam, and three-dimensional cantilever beam, etc. The final optimization results show that the platform can find the appropriate material distribution in the design and within the constraints of the target material volume to complete the topological optimization design of stress minimization.

The development of this design platform solves the existing BESO method's application problem of stress optimization under irregular grid, and provides a new way for combining academic theory of topology optimization with engineering practice. At the same time, it also provides a new idea for the research of topology optimization method, which has reference significance.

Key words: BESO method, topology optimization, irregular element, ANSYS, stress minimization

目 录

第1章 绪论 1

1.1 研究目的及意义 1

1.2 国内外研究现状 1

1.3 主要内容及技术方案 3

第2章 BESO算法概述 4

2.1 应力最小化设计的数学模型 4

2.2 BESO法敏度值处理 5

2.3 BESO法变量更新方案 6

2.4 本章小结 7

第3章 设计平台的具体实现 8

3.1 ANSYS有限元建模与有限元分析 8

3.1.1 有限元建模 8

3.1.2 有限元分析 9

3.2 参数传递 9

3.3 Matlab代码 10

3.3.1 主体函数（101行） 10

3.3.2 前处理子函数（88行） 11

3.3.3 过滤权重因子子函数（20行） 11

3.3.4 变量更新子函数（36行） 12

3.4 本章小结 12

第4章 数值模拟应力优化算例 13

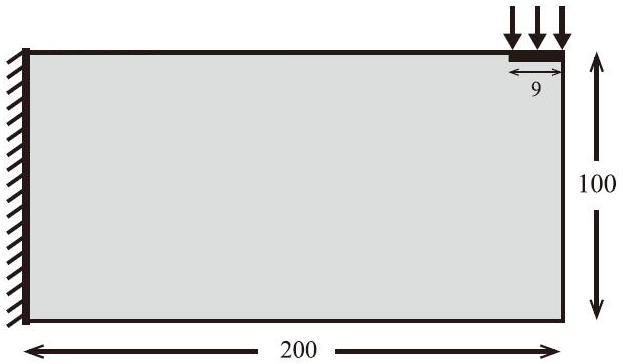
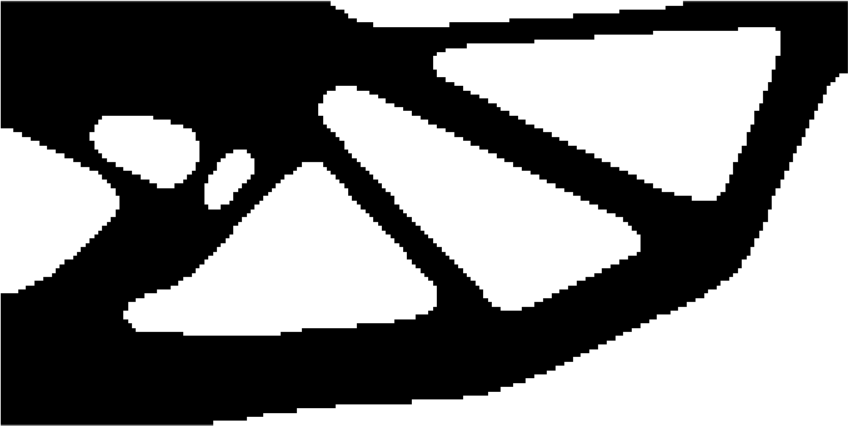
4.1 二维悬臂梁 13

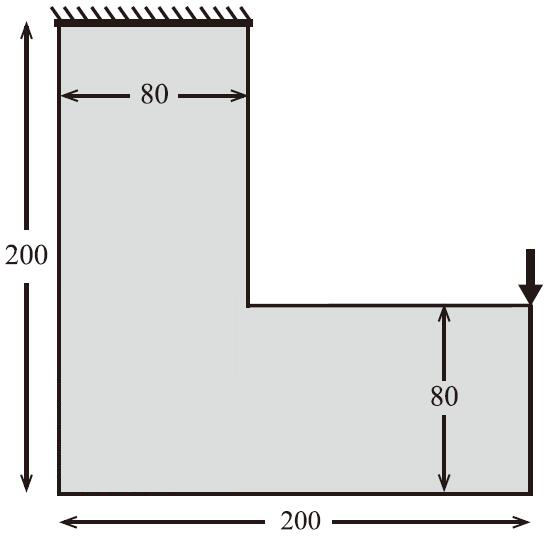
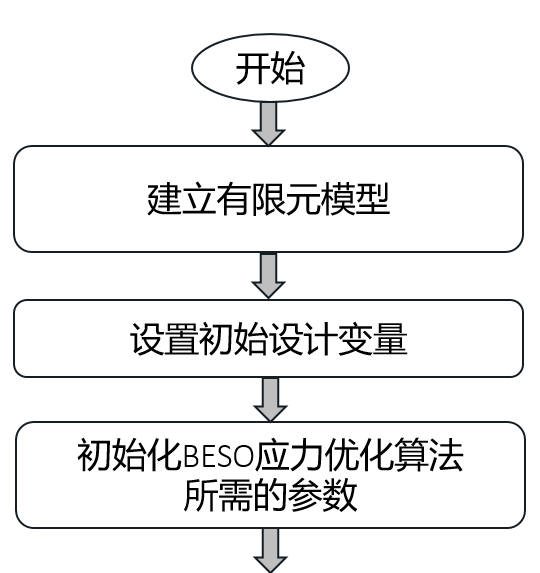
4.2 二维L型梁 15

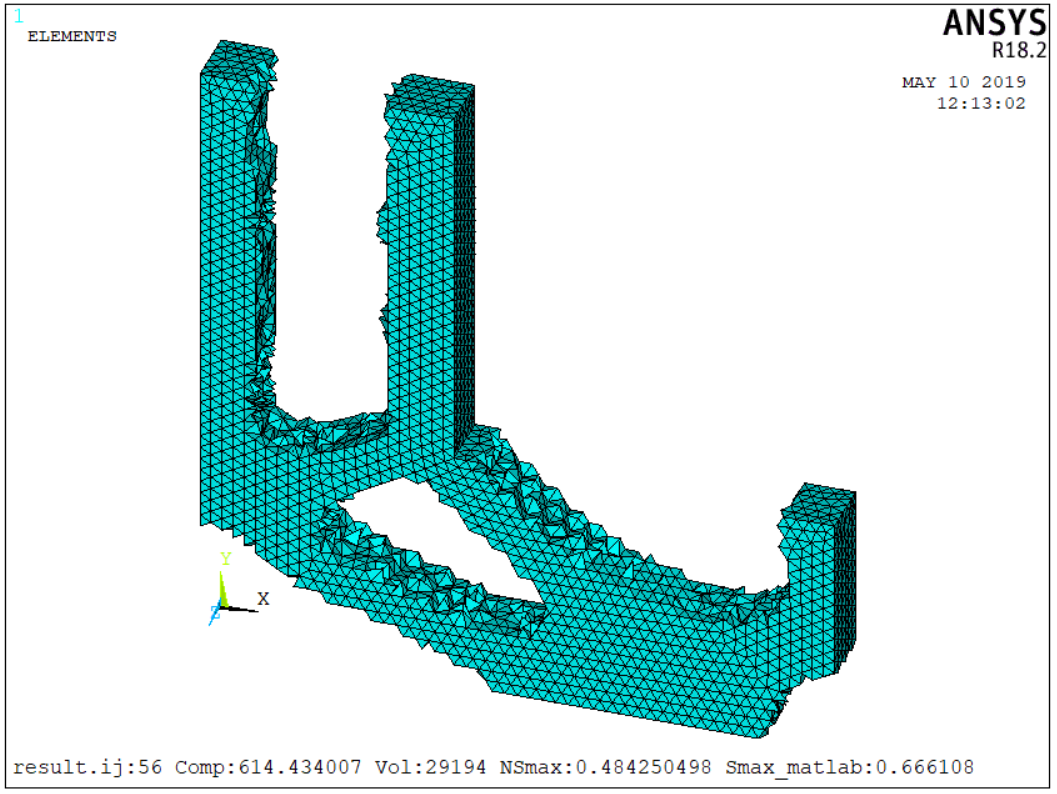
4.3 三维L型梁 17

4.4 三维悬臂梁 19

4.5 实际工程应用 21

4.6 本章小结 24

第5章 结论 25

参考文献 26

致 谢 29

附 录 30

附录A： 有限元建模ANSYS命令流 30

附录B： 有限元分析ANSYS命令流 34

附录C： Matlab主函数 38

附录D：Matlab前处理函数 41

附录E：Matlab过滤权重因子函数 44

附录F：Matlab变量更新函数 45

附录G：有限元分析云图 46

第1章 绪论

1.1 研究目的及意义

此次毕业设计题目为《基于BESO法的拓扑优化设计平台开发》，此次开展的工作主要是运用MATLAB搭建一款基于BESO应力优化算法的优化平台，该平台的大致工作流程与BESO算法类似，所不同的是将BESO算法中有限元建模与有限元求解的两个步骤通过调用ANSYS实现，BESO算法中所需的一些参数也可直接通过ANSYS读取出来，最终能实现二维悬臂梁、二维L型梁、三维L型梁，以及实际工程零件等的应力优化设计。

BESO算法是在众多拓扑优化算法中比较主流的算法，它在非线性材料及大变形^[1]-[2]、刚度及频率优化^[3]、多材料^[4]、能量吸收^[5]、周期结构^[6]-[8] 、多重约束^[9]等问题中应用性能表现出色。在网格独立、收敛的BESO法提出后，夏凉等^[10]在2017年的一篇综述对BESO法进行了一次完整的总结，2018年又运用BESO法解决应力最小化优化问题^[11]，并提供了一系列经典拓扑优化案例实现的参考代码。其中包括二维悬臂梁、二维L型梁、二维预置缺口的MBB梁、三维悬臂梁等在不同P范数条件下实现应力最小化的优化代码，为拓扑优化进一步研究提供了新的思路。我们知道，MATLAB是计算功能强大的矩阵实验室，但并非建模软件，而ANSYS是有限元建模与求解功能强大的有限元分析软件，将两者结合起来可实现在异形网格下更为复杂的三维零件的优化，为工程实际零件的设计提供了可能与方便。无论是对于刚度优化问题还是应力优化问题，或者是多重约束下的刚度或应力优化问题，各种算法中有限元分析所需的单元节点编号、坐标、单元体积、应力、柔度及其对设计变量的敏感度等单元信息众多，但这些参数均可由ANSYS有限元求解后直接导出传输给MATLAB。而规整网格与不规整网格的相应参数转化关系的理论在有限单元法知识中早已被总结。因此，此次毕业设计以应力最小化的扩展BESO法为基础，搭建MATLAB-ANSYS结合的优化设计平台，实现不规整网格有限元模型的应力最小化优化问题。

1.2 国内外研究现状

结构优化是通过调整结构的尺寸、形状及拓扑构型来提高结构的强度、刚度等多方面性能，同时保证结构的制造便利性的优化方法，有利于实现轻量化设计。

拓扑优化，其作为结构优化类型中的一种，其设计理念改变了传统尺寸优化和形状优化的设计模式，通过去除冗余的材料来实现构型的创新设计，初步展现出可观的工程应用价值。拓扑优化算法发展了一百多年，澳大利亚Michell^[12]提出了早期的拓扑优化算法，即借助桁架布局的最优标准来实现轻量化设计。Rozvany等^[13]-[15]在70年后将上述桁架理论进一步延伸，提出桁架在网格结构下进行优化的方法。伴随着计算机硬件及数值计算方法的发展，拓扑优化算法研究逐渐被抬出水面，拓扑优化开始逐渐受到国内外学术界及业界的广泛关注，均匀化算法^[16]、渐进结构算法^[17]-[18]、泡沫算法^[19]、水平集算法^[20]、变密度算法^[21]-[22]、拓扑导数算法^[23]、相场算法^[24]及隋允康等学者提议的独立连续映射算法^[25]等主流算法也应运而生。而其中的渐进结构优化算法，简称ESO算法，也经历了一段时期的完善与发展。最开始Xie等^[17]-[18]提出的ESO算法，是在迭代循环中一次次进行有限元分析，求解目标函数对拓扑设计变量的敏感度值，并依据变量更新算法将低效的单元逐渐去除。因删掉的单元将不再被找回恢复，ESO法也被称为硬删除法。其后，为解决单元一旦被删除无法再被找回的问题， Querin等^[26]-[28]对ESO算法进行完善并提出双向渐进结构优化算法，简称BESO算法，BESO算法可删除低效单元的同时找回高效单元，避免了前期被删除的单元在后面的迭代循环中无法被恢复的问题。黄晓东和谢亿民^[29]对BESO法进一步完善，提出网格独立的BESO法，通过对敏感度进行过滤避免网格依赖，将敏感度与历史值平均稳定优化过程，为非线性材料及大变形^[1]-[2]、刚度及频率优化^[3]、多材料^[4]、能量吸收^[5]、周期结构^[6]-[8] 、多重约束^[9]等问题提供了新的解决思路。实现网格独立的BESO算法具有高效的优化性能和良好的收敛性与鲁棒性，被广泛应用于学术研究和工程上。BESO法后来应用于应力优化中，Le等人已经总结了应力优化中的三个挑战^[30]，分别为奇异性问题、局部应力问题和高度非线性的应力现象。奇异性问题，是指低密度单元意味着具有高应力，使得优化算法无法去除这些单元，一般的补救方案为解除应力约束，使单元的应力与密度同时减少；局部应力问题，是指应力为一个局部量，设计中应控制连续结构各处的应力，常通过P范数应力或KS函数得到的全局量来近似最大应力，此方法计算应力对拓扑变量的敏感度数值效率较高，但无法对局部应力充分控制；高度非线性应力现象，是指由于应力对拓扑变化高度敏感，在优化中应力极大地受到其邻近密度变化的影响，这个现象在尖角结构处更加明显，Le等提出采用密度过滤和敏感度过滤来考虑稳定性。BESO法应用于应力最小化设计时，BESO算法的离散特性很自然的避免了变密度法中众所周知的“奇异性”问题，将P范数整体应力测度对拓扑变量的敏感度进行过滤并与历史值平均便可高效地实现二维、三维情况下基本案例的应力最小化设计。

现如今，拓扑优化设计理念已得到广泛的认可，一些典型的商业软件工具也具有拓扑优化基本模块，比如，Altair-Optistruct、FE-Design-TOSCA、Quint-Optishape、Ameda、VR及D-Genesis等。其中，Tosca和Optistruct均利用变密度法实现各种不同工况下的多种目标的优化，Ameba利用BESO法实现刚度优化。Tosca更倾向于依据给定工况优化出高性能目标模型、Optistruct倾向于对优化过程的细节处理、Ameba可直观呈现优化过程的拓扑构型。Altair HyperWorks是业内最全面、开放的架构CAE仿真平台，而其中的Altair Optistruct是业界公认的功能最强的结构分析及优化求解器，可用于概念设计和细化设计。

1.3 主要内容及技术方案

夏凉等^[9]提供的一系列BESO法应力优化代码，将其中的有限元建模与有限元分析变更为调用ANSYS命令流完成，有限元求解后的单元应变能、应力等参数可直接传输给MATLAB中，无需在MATLAB中进行复杂的公式计算。为适应不规整网格情况，将代码中单元形函数矩阵（N矩阵）、几何矩阵（B矩阵）等的计算公式一般化。而MATLAB中完成设计变量更新后可直接反映在ANSYS中的三维模型中，直观呈现出整个优化过程。

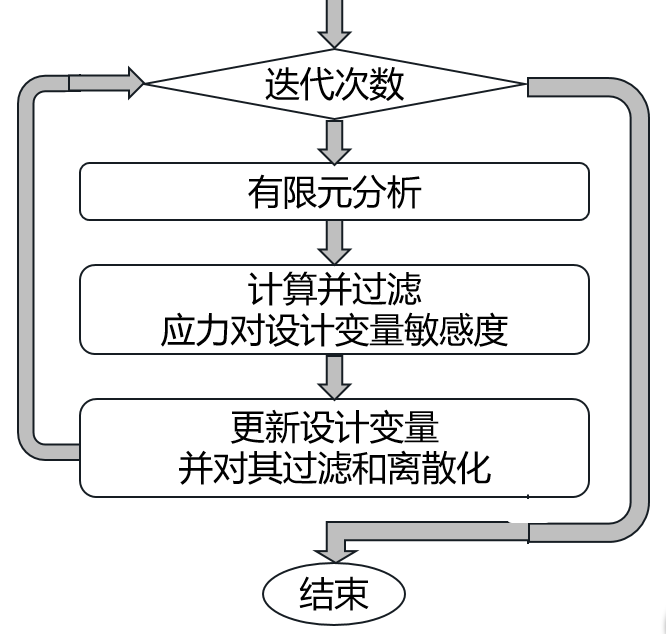
此优化平台的程序执行流程如图1.1所示，其中，有限元建模、有限元分析由MATLAB程序调用ANSYS完成，建模中单元刚度矩阵、节点信息以及求解后的应变能、应力等参数通过txt文件的写入与读取的形式传递给MATLAB，在MATLAB中计算不规整单元的形函数、B矩阵等参数，迭代循环中调用ANSYS进行有限元分析，求解并过滤应力对设计变量的敏感度数值，设计变量在BESO法中更新后进行过滤离散化，然后也通过txt文件传递给ANSYS程序，每次迭代优化通过ANSYS生成的图片，直观呈现整个优化进程。迭代结束后，在ANSYS有限元求解的solve.db文件中将会得到优化后的最终模型。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：