摘 要

人类对于海域的探索已经渗透到遥远的海洋环境中。为了保证勘探过程中工作环境的安全和良好，有必要减少浪潮、消减波浪。对于码头、港口、海岛和栈桥的防护和维修工程，防波堤的研究则能很好地解决这个问题，在此基础上，防波堤结构形式的选取显得尤为重要。具有低廉的造价、环境友好、结构便于安装和移动、有效的消波性能以及较低的海底地质要求等诸多优点的防波堤越来越受到大家的关注。

现如今实际工程中加强浮式防波堤主体消浪效果的主要手段，一是加大浮箱延入射波浪传播方向的宽度，二是在浮式防波堤底部添加能够辅助消浪的部件，但是要想在实际工程中实施这些构想是很困难的事。本文将采用软件建模、数值模拟的研究方法探讨坐底式箱形防波堤和浮式箱形防波堤的消波性能，对各种形式的防波堤构型逐一进行优化。

通过AQWA软件模拟，得到两种箱形防波堤的结构模型。通过水动力分析软件AQWA对重点研究的防波堤结构在频域下分析透射系数，在时域下研究模型六个自由度的运动响应和锚泊系统例如锚链的相应的参数。

关键词：箱形防波堤；透射系数；消浪特性；数值模拟

Abstract

Human exploration of the sea has penetrated into the remote marine environment. In order to ensure the safety and good working environment in the exploration process, it is necessary to reduce the wave and reduce the wave. For the protection and maintenance of wharfs, ports, islands and trestles, the study of breakwater can solve this problem well. On this basis, the selection of breakwater structure is particularly important. More and more attention has been paid to breakwaters with many advantages, such as low cost, friendly environment, easy installation and movement of structures, effective wave attenuation performance and low seabed geological requirements.

Nowadays, the main means to enhance the effect of wave attenuation of the main body of the floating breakwater in practical engineering are to increase the width of the pontoon extending the direction of incident wave propagation and to add components to the bottom of the floating breakwater which can assist in wave attenuation. However, it is very difficult to implement these ideas in practical engineering. In this paper, the research methods of software modeling and numerical simulation will be used to study the wave dissipation performance of bottom-sitting box breakwater and floating box breakwater, and to optimize the configurations of various types of breakwater one by one.

Through AQWA software simulation, two structural models of box breakwater are obtained. Through the hydrodynamic analysis software ANSYS-AQWA, the transmission coefficient of the breakwater structure is analyzed in frequency domain, and the motion response of the model with six degrees of freedom and the corresponding parameters of the mooring system, such as the anchor chain, are studied in time domain.

Key Words：Box breakwater; transmission coefficient; wave dissipation characteristics; numerical simulation

目录

第一章 绪论 1

1.1 选题的背景及意义 1

1.2 浮式防波堤结构形式及消浪特点 2

1.3浮箱式防波堤研究现状及成果 2

1.4本文的主要研究思路与研究内容 3

第二章 势流理论 5

2.1水波问题的控制方程 5

2.2水波问题的边界条件 5

2.2.1自由面条件 5

2.2.2物面条件 6

2.2.3底面条件 6

2.2.4无穷远处条件 6

2.3 Cummins方程 6

2.4波浪透射系数的定义 6

第三章 坐底式箱形防波堤的数值模拟研究 8

3.1坐底式箱形防波堤模拟过程 8

3.1.1 WORKBENCH AQWA界面介绍 8

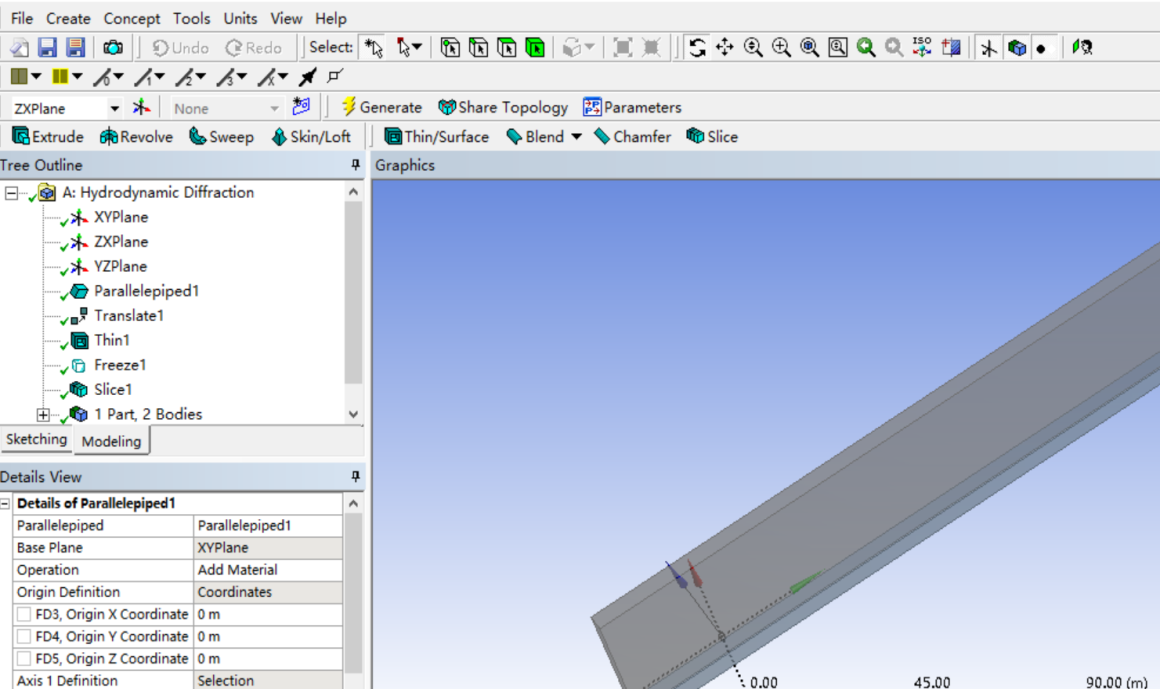
3.1.2 WORKBENCH AQWA建模介绍 9

3.2坐底式箱形防波堤模拟结果分析 10

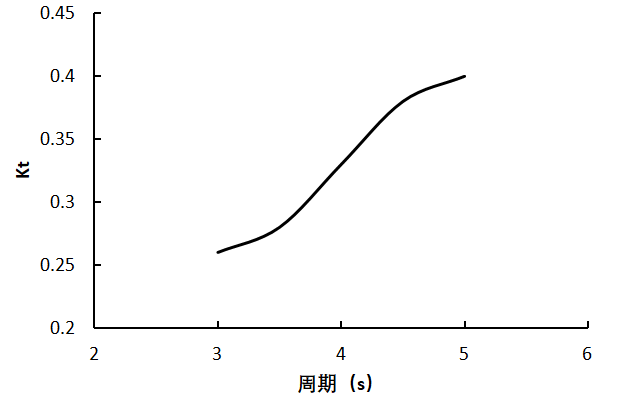
3.2.1 周期对坐底式防波堤透射系数的影响 10

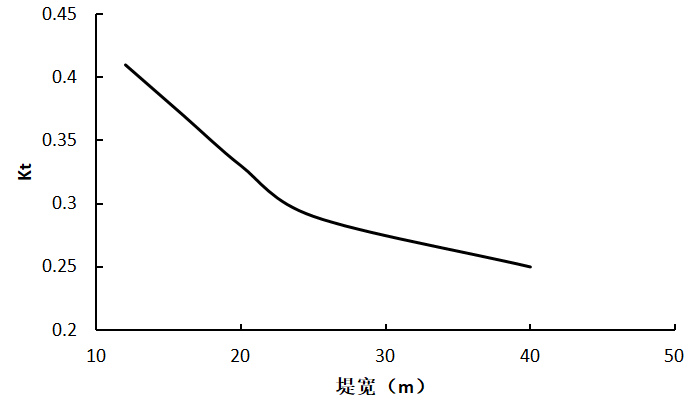
3.2.2 堤宽对坐底式防波堤透射系数的影响 11

第四章 浮式箱形防波堤的数值模拟研究 12

4.1浮式箱形防波堤模拟过程 12

4.2 浮式箱形防波堤模拟结果分析 13

4.2.1 实体模型相关参数 13

4.2.2 模拟工况及参数 14

第五章 消浪性能的优化 19

5.1 浮式箱形防波堤和坐底式箱形防波堤的比较 19

5.1.1 两种防波堤数值模拟比较 19

5.1.2 浮式防波堤的优缺点 19

5.2 浮式箱形防波堤消浪特性的优化 20

5.2.1 自由状态下改变箱体的宽度 20

5.2.2 自由状态下增加箱体数目 20

5.2.3 锚泊状态下改变锚链的初始张力 22

5.2 本章小结 23

第六章 结论及展望 24

6.1 全文总结 24

6.2 展望 24

参考文献 26

致 谢 28

第1章 绪论

1.1 选题的背景及意义

当前，人类社会活动和经济活动的发展快速，土地资源和空间不能完全满足社会进步发展的需要。海域不仅仅占地球整个表面积的70.9%，而且蕴含着大量的人类资源：矿产和生物资源、水资源等能源资源。海洋正在逐步成为我们人类的另一个生存空间。人类迫切需要探索广阔的海洋。海洋资源的开发使用和保护将面临一个新的快速发展和无比繁荣的时期。在开发公海的过程中，必须具备稳定的海洋条件和安全良好的工作条件，才能更好地工作。一些不利的海上条件是我们迫切需要解决的问题^[4]。

在港口和沿海工程中，防波堤结构通常安装在建筑物的前部。防波堤通过已经安装固定的机制消抵抗波浪，以确保路堤后面的环境稳定。确保船舶安全平稳停靠和港口建筑物的正常运行。除此之外防波堤也可以在港口和岛的周围建造，以覆盖防波堤内区域，同时防止港口内海岸线的淤积和波浪侵蚀。

通过实验和长期理论积累分析，研究人员发现，在大致为波高的2-3倍水层厚度内集中了波浪的大部分能量。由此浮式防波堤应运而生，漂浮在水面的浮式防波堤能更好地适应波能分布特点。尤其在向远海的探索中，传统固定式的防波堤已不再适用，浮式防波堤则能更好地发挥抗浪的作用。

人类在很早之前就发现漂在水体表面上的物体会降低波浪强度。大型船舶在海上停泊时，船体后浪高会降低，海上浮冰也会降低波浪能量。最近几年以来，浮式防波堤引起了全球各地各领域科学家的重点关注。更多的项目工程开始使用浮式防波堤来抵抗海浪。随着科学技术的不断进步，浮式防波堤的形式也越来越全面化多样化，消波性能也得到了很大的进步^[7]。

南海的海域上在台风暴雨季节风浪极其肆虐，为了确保礁上所造浮动码头和栈桥的稳定和安全，在近海水域的外围布置浮式防波堤很好的解决了这个问题。浮式防波堤具有结构简单，造价低廉，对地基的要求不高，运输和安置便捷等优势，有效的保护了码头的稳定性和栈桥的安全性。

本文主要研究浮式箱形防波堤和坐底式箱形防波堤的消浪特性，可以对防波堤的总体布局、堤型设计和挑选等进行优化。掌握各类型防波堤主体布置和优化构型等技术，能够为我国南海事业提供牢靠的理论和技术支撑，该研究具有实际意义与操作价值。

1.2 浮式防波堤结构形式及消浪特点

浮式防波堤从基本结构形式角度分类主要包括浮箱式防波堤、浮筒式防波堤和浮筏式防波堤。

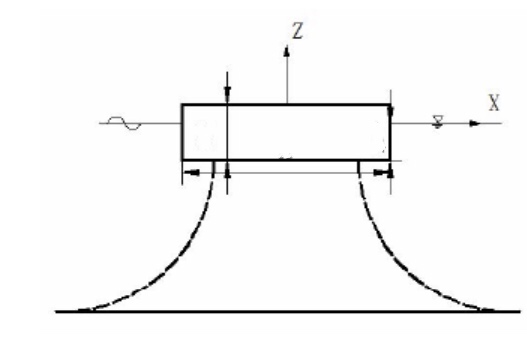
浮箱式防波堤:由多个箱体连接而成的浮式防波堤是实际工程中应用最多的浮式防波堤(如图1.1)。浮箱式防波堤箱体的制作材料一般为混凝土或钢筋混凝土，其断面形状多为矩形、梯形和菱形。浮箱式防波堤设计简单、施工安装便捷、建设周期短、造价较低，并且方箱可预制而成易于控制。浮箱在消浪的同时，浮箱表面可作为道路供人车行驶，浮箱内部可作为仓库储存货物。

浮箱式防波堤设计简单、施工方便快捷、消浪效果较好，是目前实际工程中应用最为广泛的浮式防波堤结构形式。国内外学者也对浮箱式防波堤进行大量的实验和理论研究，取得了很多成果^[7]。

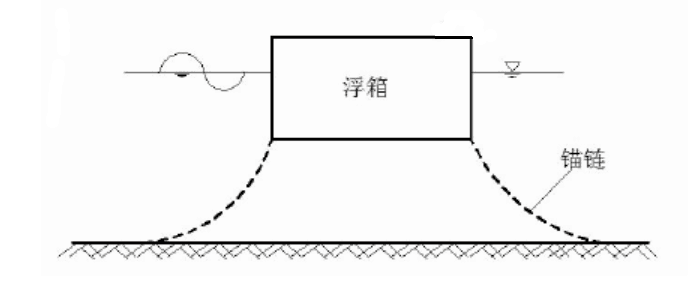
图1.1 浮箱式防波堤整体构型

1.3浮箱式防波堤研究现状及成果

我国学者姚国权^[4]通过将浮箱前壁划分为开口和密封两种形式，对矩形方盒浮式防波堤进行了改进。通过在浮箱内增加一个小的浮箱，在浮箱中增加了诸如胸墙、波板和瓦楞纸板等附加结构。为了改变浮箱的倾斜角和吃水，系泊形式采用锚链锚固和桩堵两种形式。这些方法结合起来形成了十个不同的浮式箱形防波堤形式。通过物理研究分析出了十种浮式箱形防波堤结构在规则波作用下的消浪性能，选择了具有最佳消波效果的结构形式。结果显示，采用柱塞式系泊和前壁开口的浮式箱形防波堤的透射系数最小。

盛祖银和孙龙口^[4]对浮式箱形防波堤进行了物理研究。结果表明，矩形方箱主体的迎浪面积是浮式箱形防波堤透射系数的决定性因素。箱体的宽度和吃水深度可以有效降低波浪高度。然而有矛盾的是，当方箱阻挡水的面积很大的时候，作用在主体上的波压增加，使得箱形结构不稳定。

候勇^[4]研究的是单方箱防波堤，方箱由锚链固定在底部，入射波设置为规则波。研究结论显示波浪透射系数随着方箱宽度的增大是先减小后增大的，在此研究基础上能够获得防波堤的最佳宽度。实验结果还表明了锚链在不同工作条件下的应力值，总结了单浮式防波堤特性与锚链强度的关系^[7]。

张伟^[4]运用ANSYS-AQWA模拟软件，在条件不同的波浪的作用下对浮式箱形防波堤进行数值模拟研究，结果显示:浮式箱形防波堤的透射系数随水深的变化不大。在规则波浪作用下，浮式防波堤由于运动响应在平衡位置附近做周期运动；在不规则波浪作用下，随着水深的增加，浮式防波堤消浪效果略微减弱，但总体上幅度变化很小。与传统坐底式防波堤相比，浮式箱形防波堤睡着水深的增大，工程成本的增量并不大但消波效果大体不变。

沈文君^[4]通过ANSYS-AQWA数值模拟软件模拟了某种形式较为特殊的防波堤 ——呈“开”字型，并研究了在规则波浪下的该种防波堤的运动响应和消浪特性，讨论了改变吃水、相对吃水和水深对浮式防波有何影响。结果表明:改变上述条件对防波堤的消波性能有一定的影响。

我国学者郑永红^[4]研究了在无限水深和有限水深条件下水面下矩形浮式防波堤的辐射和散射。通过展开特征函数和分离变量的方法，得到了函数绕射解。从绕射势和入射势出发，导出了波透射系数公式。

严建国^[7]等利用特征函数得到速度势，建立相应的防波堤模型，在此基础上对浮式箱形防波堤进行数值计算。根据波速势的变化得到了堤坝的破波性能，并从浮箱的移动走势分析防波堤的水动力特性。结果显示模型求解准确。

基于微波长和频域理论，冯宏四^[7]对矩形防波堤进行了分析计算，建立了浮式箱形防波堤计算透射系数的模型。应用模型，充分讨论了象箱形主体上方箱在六个自由度方向上的位移与波浪高度的关系^[4]。

1.4本文的主要研究思路与研究内容

本文主要的研究是通过数值模拟软件，研究坐底式箱形防波堤和浮式箱形防波堤周围的波浪场。通过软件数值模拟求解的方法对防波堤的类型没有限制，但是这种方法的缺点是整个运转流程相对复杂棘手，它一次性只能求解一种特定结构构型的防波堤，不同构型的防波堤在求解的时候需要重新建模、划分网格、运行然后进行新的时域分析，这些操作下来十分的消耗时间。本文的主要研究工作是应用软件ANSYS-AQWA模拟防波堤（坐底式箱形、浮式箱形）。

本文研究大体思路如图所示：

图1.2 论文研究思路

本文主要分为如下六章：

第一章：绪论，主要是介绍该篇论文选题的目的背景及意义、浮式防波堤结构的特点以及浮式防波堤的研究现状及成果，对这些学者的课题研究进行了分析，进一步分析确定了该论文的研究思路和大体方向；

第二章：主要介绍了浮式防波堤分析理论拉普拉斯方程、边界条件和波浪的运动方程；

第三章：主要介绍了应用数值模拟软件研究坐底式箱形防波堤的波浪场，计算分析了周期等因素对传统坐底式防波堤透射系数的影响，研究其消浪特性；

第四章：主要介绍了浮式防波堤的数值模拟研究，分析了周期、锚链等外界因素对浮式箱形防波堤消浪性能的影响；

第五章：分析比较了上述两种形式防波堤的优缺点，并针对防波堤本身的特性例如改变堤宽、改变锚链张力来优化防波堤的消波性能，是设计出来的防波堤达到最优状态；

第六章：对整篇论文的结论进行了总结并对论文中还未涉及到或者研究不完善的地方提出了研究期望^[1]-[5]。

第2章 势流理论

第二章会在势流理论的基础上，模拟箱形防波堤与波浪之间的相互作用以及周围的波浪场。该章将重点介绍水动力学在势流理论里的基本方程，包括解决水波问题所需要借助的自由面条件、物面条件、无穷远处条件。

2.1水波问题的控制方程

在求解重力水波与浮体物相互作用的过程中，取没有扰动的xoy平面为直角坐标系，z 轴垂直向上，坐标原点放在静水面。忽略不计水的密度变化，假定水体是不可压缩。因此流体运动符合质量守恒，在笛卡尔坐标系下可以将方程表示为:

（2.1）

其中：；表示为流体质点在(x,y,z)处的速度矢量；在无旋流动中，速度v可以理解为速度势的梯度，速度势在这个地方为标量，因此流体质点速度又可以表示为:

（2.2）

所以，质量守恒要求速度势标量满足拉普拉斯方程,理想流体的运动方程可以表示为:

（2.3）

拉普拉斯方程还可以表示为：

（2.4）

2.2水波问题的边界条件

速度势在流体域边界上满足的条件称为边界条件。边界条件可以是在物体的表面，也可以是两种不透水流体的边或者远方的边界等。边界条件是求解上述提到的速度势问题的关键，拉普拉斯方程所需要满足的条件为:自由表面条件、物面、底面以及无穷远处条件。

2.2.1自由面条件

设是以z轴为自由面的值，因此自由面条件可以用下列方程表示：

F=z-=0 （2.5）

2.2.2物面条件

表面条件并不普遍，流体不能穿透物体的表面。 当满足以下两个条件即流体不会离开物体的表面以形成空隙和物体表面的法线方向时，流体的速度应该等于物体运动的速度：

（2.6）

为物体的法向速度，为物体的表面。如果是探讨绕射问题，在物体固定不动即=0，则物面条件为:

（2.7）

2.2.3底面条件

在z=-h(x，y)的海域底部，流体不能穿过：

（2.8）

其中为法线方向。通过方程F=z h(x，y)=0可以将底面条件表示为：

（2.9）

2.2.4无穷远处条件

无穷远处条件因为坐标系的选取不同有两种表达方式，第一种选择大地坐标系，边界条件可写为→0 (R→∞) R为物体与无穷远处质点的距离值；第二种选择随体坐标系，无穷远处条件可以表示成=v (R→∞)^[4][7][8]。

2.3 Cummins方程

基于Cummins方程的时域运动方程可以写为：

（2.10）

这里，m是质量矩阵,是附加质量矩阵；代表波浪辐射对机体产生的作用力；表示静水力；表示波浪激振力；表示粘性阻力；表示外部作用力（例如动力输出系统和系泊系统力）。

2.4波浪透射系数的定义

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：