摘 要

在现实中，有许多实际问题可以归结为优化问题，对于诸如产品设计、路径分配规划等此类复杂的优化问题，通常需要优化的目标函数有多个，而且这些函数之间很可能是相互冲突的，同时可能需要融入决策者偏好解决该类问题。除此之外，许多优化问题的优化目标不仅仅只有一个，工程师需要根据实际情况对具体问题的多个目标进行同时优化。对于此类问题的解决方法，科学家们从传统的算法里逐渐发展出了适合解决此类问题的多目标优化进化算法。随着进化算法的日趋成熟和完善，此类复杂的优化问题可以很好地被解决，进化算法也被赋予了重要的理论意义和实际应用价值。

本毕业设计针对路径规划配送问题进行MATLAB建模仿真，定义模型、车辆、路线和服务窗口限制等相关参数，利用遗传算法和粒子群算法分别仿真分析，得到最佳路径的分配结果和预算，并根据仿真的算法收敛图对比遗传算法和粒子群算法的相关性能。

通过测试，证明本文所设计的路径分配规划问题可以很好地得到较优的结果，并保证结果的可行性与完整性。并对基于区间参数多目标优化的问题进行总结，同时阐述各多目标优化进化算法的优点，对NSGA-Ⅱ和粒子群算法的优点比较。

关键词：区间参数，多目标优化，遗传算法，粒子群算法

Abstract

Many practical problems can be summed up as optimization problems, for complex optimization problems such as product design, path allocation planning, and so on, there are often multiple objective functions that need to be optimized, and the objective functions may be conflicting, and may need to be integrated into the preferences of decision makers to solve such problems. In addition, there is more than one optimization goal for many optimization issues, and engineers need to optimize multiple goals for specific issues according to the actual situation. For the solution of such problems, scientists have gradually developed a multi-objective optimization evolutionary algorithm suitable for solving such problems from the traditional algorithms. With the maturation and perfection of evolutionary algorithms, such complex optimization problems can be solved well, and evolutionary algorithms also have important theoretical significance and practical application value.

This graduation design carries on the MATLAB modeling simulation to the path planning distribution problem, defines the model, the vehicle, the route and the service window limitation and so on related parameters, uses the genetic algorithm and the particle Swarm algorithm respectively simulation analysis, gets the best path distribution result and the budget, According to the simulation algorithm convergence graph, the correlation performance of genetic algorithm and particle swarm algorithm is compared.

Through the test, it is proved that the path allocation planning problem designed in this paper can get better results well and ensure the feasibility and completeness of the results. The problem of multi-objective optimization based on interval parameters is summarized, and the advantages of each multi-objective optimization evolutionary algorithm are expounded, and the advantages of NSGA-Ⅱ and particle swarm algorithm are compared.

Keywords: Interval parameters, multi-objective optimization, genetic algorithm, particle swarm algorithm

目 录

第1章 绪论 1

1.1目的及意义 1

1.2国内外现状 1

1.3课题研究内容与目标 2

第2章 优化关键技术研究 4

2.1区间参数 4

2.2多目标优化 4

2.2.1帕累托最优解 5

2.2.2多目标优化方法 5

2.3非支配排序遗传算法 6

2.3.1NSGA运算过程 6

2.3.2NSGA的特点 7

2.4 NSGA-Ⅱ算法 8

2.5粒子群算法 9

2.6本章小结 10

第3章 基于路径优化的建模设计 11

3.1模型需求背景 11

3.2研究假设和模型设计 11

3.2.1研究假设 11

3.2.2模型建立 12

3.3模型相关参数 12

3.3.1参数设计 12

3.3.2决策变量 13

3.4数据分析 13

3.4.1车辆的运输成本 13

3.4.2货物损耗成本 13

3.4.3 配送车能耗成本 14

3.4.4碳税成本 14

3.4.5超出时间窗惩罚成本 14

3.4.6时间满意度 15

3.5本章小结 15

第4章 路径优化模型实现与分析 17

4.1 数据定义 17

4.2遗传算法优化求解 18

4.2.1选择交叉变异 18

4.2.2遗传算法结果输出 19

4.3粒子群算法优化求解 19

4.3.1 初始化局部最优和全局最优 19

4.3.2粒子群算法结果输出 20

4.4算法对比 21

4.5本章小结 22

第5章 总结与展望 23

5.1总结 23

5.2展望 23

参考文献 24

致谢 25

第1章 绪论

1.1目的及意义

近半个世纪以来，基于区间参数多目标优化的问题越来越广泛。实际问题中，获取随机变量满足的分布或描述模糊数的隶属函数通常是很困难的，因此此类问题求解也是比较困难的。正因于此，科学家们研究出了模拟自然界生物进化和遗传变异机制而形成的一种全局搜索算法——进化算法，在解决此类复杂的优化问题时，表现了十分突出的优越性能。同时，追求最优求解是工程师和科学家们共同的目标，遗传算法对于各行各业的多目标优化问题都有着深刻的应用前景。

和生活息息相关的，例如生产过程、产品规划、利润最大化、机翼设计、存储系统、路径规划、网络优化、车辆调度等问题，都可以利用基于区间参数多目标优化问题的遗传算法进行求解，同时融入决策者偏好解决该问题，这些对于本课题的研究都有很大的研究背景和应用前景。

尤其在工业中的应用，基于区间参数多目标优化的解决方法应用广泛。由其带来的社会利益是巨大的，在工业生产中，在减少成本的基础上尽可能实现加速生产的要求，在路径分配中，保证条件的同时要尽力减少成本等等，这些都给工业生产带来直观的利益。由此可见，基于区间参数多目标优化问题的遗传算法的研究、设计与实现至关重要，直接关系到我们生活或者工业企业的生存与发展，成为日待解决的重点问题。

1.2国内外现状

基于区间参数多目标的优化问题一直是国内外的工程师和科学家们非常重视的研究方向，而且进化算法是模拟自然界生物进化和遗传变异机制而形成的一种全局搜索算法，在解决复杂的优化问题时，能表现出优越的能力。因此将二者合而为一地解决多目标优化问题是各国工程师的所共同面对的难题。早期由于技术不发达，解决多目标优化问题的方法有很大的局限性，而且解决方案也不够理想过于冗余。随着对进化算法的深入研究，在传统的简单的遗传算法的基础上，加入了新的算法途径，如进化算法（EA）、粒子群算法（PSO）、人工免疫系统（AIS）和蚁群算法（ACO）等等。国内外的研究人员通过加入高度并行性、自组织、自学习与自适应等自然特征的算法思想，提出了多种多目标遗传算法，其中效果最好的是非支配排序遗传算法NSGA，随着应用和研究的不断深入，NSGA也慢慢显现出其弊端，科学家们通过数以万计的实验和应用，不断地改进算法，将 NSGA的弱点不断地克服，最后研究出了带精英策略的非支配排序遗传算法NSGA-Ⅱ。

国内相较于国外，对带精英策略的的非支配排序算法的研究的数量过少。无论是理论研究还是应用的深入，国外工程师和科学家所涉及的范围都远超过国内。但这并不意味着我国的基于区间参数多目标优化问题的遗传算法的研究技术远低于国外，随着科学技术的发展，利用遗传算法在解决区间参数多目标优化方面的问题时的效率，将得到大大提高。从农业生产到能源控制，从金融贸易到通信国防，各行各业都有着优化应用的实例，美国Bell飞机公司为了对机翼进行优化处理，对其标注了上百个设计变量进行算法优化，使得在保证飞行质量的前提下将机翼的质量减小了三分之一；无独有偶，美国对大型航空母舰也根据其特点对其标注了十个变量进行优化处理，最后使得工程造价降低十分之一；还有不计其数的路径规划等都利用了基于区间参数多目标优化问题的遗传算法的研究。实践表明，此方面的研究有着实质的作用和远大的应用前景。^[1]

在工业方面，生产过程、产品规划、利润最大化、机翼设计、存储系统、路径规划、网络优化、车辆调度等多种领域都有基于区间参数多目标优化问题的遗传算法的涉及，工程师们通过遗传算法的优化优点对各领域问题进行优化求解已经非常普遍。在今后，对于此类问题的优化的普及将会越来越广泛，遗传算法也必然会随着科技技术的进步而越发精确实用，将遗传算法更好地运用到基于区间参数多目标优化问题上必将是以后的趋势。

1.3课题研究内容与目标

大量实际工程问题中存在着与材料属性、几何特性、边界条件、测量与装配误差等有关的不确定性，这些不确定性虽然在多数情况下数值较小，但其耦合作用可能使产品或系统性能产生较大偏差甚至失效。^[2]不确定性优化方法对产品进行设计时，无须对模型或参数做出较多简化和假设，可以建立更为客观和真实的优化模型，不仅可以获得最优的设计方案，而且可以使优化解在不确定性条件下仍然满足可靠性要求。因此，不确定性优化方法具有重要的理论意义和工程意义，目前已经成为先进设计领域的重要研究方向。区间优化起源于20世纪80年代初，经过近四十年的发展，成为广受关注的一类不确定性优化方法。区间优化的核心是通过区间方法表征优化模型中的所有不确定性参数，只需要知道参数的上、下边界，而非精确的概率分布或模糊隶属度函数。^[3]化在不确定建模方面相对随机规划和模糊规划具有较为突出的优点，其对样本量的依赖性相对较小，而且区间的概念简单、直观、易于工程人员理解与应用。区间优化因上述优点有望很大程度上扩展不确定性优化理论的研究对象和应用领域，从而有效提升未来复杂工程系统或产品在不确定性环境下的设计水平，其正在成长为一类与传统随机规划与模糊规划并重的主流不确定性优化方法。

对各种工程实行基于区间参数的多目标优化的思路，运用遗传算法求取最优解，是解决多目标优化问题的新方法。本次毕业设计是选用了路径配送的最优成本和使分配点用户更加满意的优化主题，对路径配送问题进行建模，同时利用遗传算法和粒子群算法分别对其进行求解，预期得到最佳成本，并将条件控制在区间参数之内。同时根据遗传算法迭代函数的收敛图与粒子群算法迭代函数的收敛图相比较，对比二者的相关性能。

第2章 优化关键技术研究

2.1区间参数

两个有序的实数组成区间数（interval number），简称区间，它不仅有集合的特性，也拥有数值特性，以区间参数为研究对象的数学分析方法称为“区间分析”或“区间数学”。最早在20世纪30年代的欧洲，英国学者就对区间算术进行了描述，同时还给出了区间的计算规则。^[4]随着时间的推移和数学技术的进步，区间运算越来越得到学术界的重视，并初步运用到实际工程领域。之后，区间分析理论不断得到各国学者的分析和发展，很快成为计算数学中不可或缺的一部分。一个有界的实数闭集称为区间：

(2.1)

在式2.1中，区间下界是上标L，区间上界是上标R，上下界组成了区间，用上标I表示。当区间两个端点刚好相等时，区间就不再是区间，而变成了一个实数。除了这种表达形式以外，区间还有另一种表达形式：

(2.2)

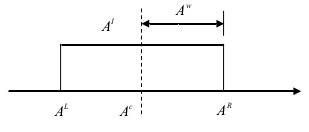式子中，上标c是区间的中点，上标w是区间的半径。下图2.1所示是区间的几何模型。

图2.1 区间的几何模型

在实际问题中，对优化问题进行建模时，由于实体系统或者环境中固有的不确定性，导致优化问题的目标函数和约束函数往往含有不确定参数，在解决此类优化问题的时候，需要事先知道所得区间的上下限或者中点和半径，规定区间范围，使得解决方案在条件允许下即区间内得以实现。^[5]

2.2多目标优化

为了避免特殊性，我们定义区间多目标最大化问题：

（2.3）

该式子里面，x是n维决策变量；x的决策空间是S；是第i个含有区间参数的目标函数；是区间向量参数；是的第k个分量；另外两个分别是的上限和下限。^[6]排除一般性，当涉及的参数全都是确定数值时，区间多目标最大化问题会退而求其次，变成确定型多目标优化问题，它的数学模型是：

（2.4）

多目标优化，即是对某一问题包含的所有目标函数同时优化。但是所涉及的目标函数之间通常情况下会相互冲突，因此，当其中一个目标函数被优化的时候，至少有一个其他的目标函数的性能会下降。所以说对于任意的多目标优化问题的求解，从来都不会有一个解让所有的目标函数都是最优的答案，取而代之的是求得一个将所有目标函数都包含在内的最优解集。^[7]多目标优化问题从结构中可以分为三个方面，分别是设计变量、目标函数和约束函数。其中在不同的工程环境中，设计变量可以根据需求而随意改变，不同的设计变量经过求解后会得到不一样的求解方案，这个也是所求得的一个优化答案。^[8]目标函数是设计者的变量所需要达到的性能指标，所有设定的这些函数就是目标函数向量。约束条件就是在设计中所不能超出的范围指标，通常用不等式表示来界定限制的范围，满足以上3个方面的解集叫做“可行解”，这些解集凑在一起就是整个优化问题的答案，其中有一个最优解来解答此多目标优化问题。^[9]

2.2.1帕累托最优解

在多目标优化算法中，由于不存在一个使得每个目标函数都占优的最优的解，因此在求解多目标问题中，往往不是获取一个最优解，而是获取一个Pareto最优解集，使得所得到的解是经过充分优化过的。所有的决策向量帕累托都不占优任何一个决策向量，这就是帕累托最优解的定义，所求得的所有解构成了帕累托最优解集和。^[10]在求帕累托最优解时，首要任务是找到一组尽可能接近帕累托最优解的解，如果不是尽可能收敛于这个最优域，那么所求的解就必定不是我们所需要的优化解。除此之外，解集还必须均匀分布，不能完全聚集在一个区域内，通过尽量分散的解才能合理地将帕累托最优域所覆盖。

2.2.2多目标优化方法

由于模拟了自然界生物进化和遗传变异机制，进化优化方法所具备的全局概率搜索方法有着和自然界生物遗传变异一致的特性，具有迭代数多，可遗传等对优化的解决有明显作用的特点。进化优化方法是通过代与代之间的迭代支撑众多解所集合的种群，进行全局搜索，由此可知，在基于区间参数的多目标优化的问题上，使用进化优化算法使得到的种群进行数代的迭代遗传进化，将会得到帕累托最优解，这就是解决基于区间参数多目标优化问题最行之有效的方法。

对于进化多目标优化算法，已经有了很多方法，例如粒子群算法，遗传算法等，其中最优秀的的算法是NSGA-Ⅱ。下面详细介绍一下这几种算法。

2.3非支配排序遗传算法

非支配排序遗传算法也称为NSGA，由于它模拟了达尔文所提出的生物进化论里的自然选择理论，并应用了遗传学里的生物进化的过程，遗传算法对于基于区间参数多目标优化问题有着得天独厚的得到最优解的优势。^[10]它由一个可能解决定义问题的解集伊始，种群里的个体由各自的基因编码所构成。各自的基因带有各自的特征，对外表现也各不相同，由于从基因到特征的映射工作比较复杂，所以使用二进制编码编码对它进行简化，让生成的初代种群经过大自然生态选择的原理，逐代进化，通过种群中的个体自我挑选基因进行组合杂交变异等操作让下一代更好地接近最优解。经过多次循环，最后得到的解可以当作定义模型问题的近似最优解。

非支配排序遗传算法是一种全局随机性的搜索算法，由于引用了大自然的进化变异特性，不存在其他函数连续性或者函数求导之类的限定，选取了概率论的优化进化方法，全自动地对结构对象进行遗传杂交变异的操作，完全自适应地调整每代子群的组合特征，使得求得的解向最优解无限靠近，就好比是自然界的物竞天择的选择条件。^[11]在自然界中，物种或者种群通过对周围环境的变化所做出的适者生存，不适者淘汰的进化法则，逐渐筛选出最适合当前环境下适应的子代，不断优化进行选择，这就启发了科学家们对人工智能中的优化算法的研究，在目标函数和条件函数中，遗传算法并不能得到收敛于全局最优解，取而代之，遗传算法只能求到收敛于局部最优的解答。