摘 要

拆卸线平衡问题由于能够缓解自然环境的压力而受到了人们的广泛关注。本文采用了基于Pareto支配的带精英策略的非支配排序遗传算法（Elitist Non-dominated Sorting Genetic Algorithm，NSGA-II）与非支配排序遗传算法（Non-dominated Sorting Genetic Algorithm，NSGA）求解拆卸同种废弃产品的拆卸序列，它能在最小化开启工作中心数量以降低成本的同时减少拆卸过程中产生危害的可能性。对上述两种算法的解集进行了比较，研究结果表明：在处理拆卸线平衡问题（Disassembly Line Balancing Problem，DLBP）时NSGA-II与NSGA相比得到的拆卸序列在目标函数上具有良好的性能。此外，当上述两种算法通过性能指标进行评价时，NSGA-II具有更好的综合性能。所得结果对于解决DLBP具有重要的指导意义。

关键词：拆卸线平衡问题；遗传算法；NSGA；NSGA-II

Abstract

The disassembly line balance problem has been widely concerned because it can relieve the pressure of the natural environment. In this paper, based on the Pareto dominance with Elitist Non - dominated Sorting based Algorithm (NSGA-II) and Non - dominated Sorting based Algorithm (NSGA) solution to remove the same waste product disassembly sequence, it can work in minimizing open center number in order to reduce costs at the same time reduce the disassembly process of the possibility of harm. The results of the two algorithms are compared. The results show that the disassembly sequence obtained by NSGA-II has better performance than that of NSGA in dealing with the disassembly line Balancing Problem (DLBP). In addition, when the above two algorithms are evaluated by performance indicators, NSGA-II has better comprehensive performance. The results obtained have important guiding significance for solving DLBP.

Key words:  disassembly line balance problem; Genetic algorithm; NSGA; NSGA-II

目 录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究目的及意义 1

1.2 国内外研究现状 1

1.3 本文研究的主要内容 2

第2章 拆卸线平衡问题定义及建模 3

2.1 问题描述 3

2.2 数学模型 5

第3章 基于GA的算法设计 7

3.1 遗传算法的基本原理 7

3.2 编码与解码方法 7

3.2.1 编码 8

3.2.2 解码 8

3.3 种群的初始化 9

3.4 适应度函数 9

3.5 变化算子 10

3.5.1 交叉算子 10

3.5.2 变异算子 10

3.5.3 修复算子 11

3.5.4 选择算子 12

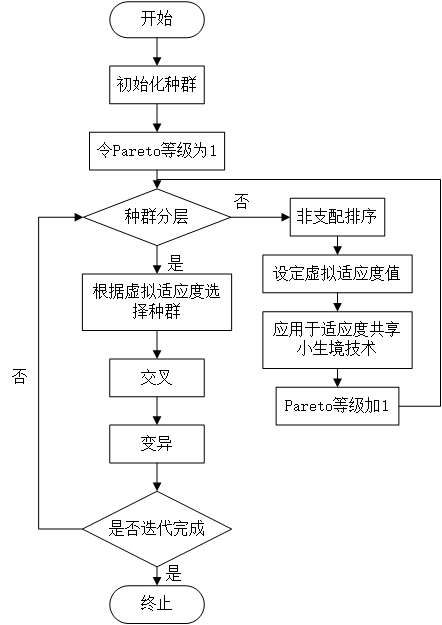
3.6 Pareto支配 12

3.7 NSGA算法 13

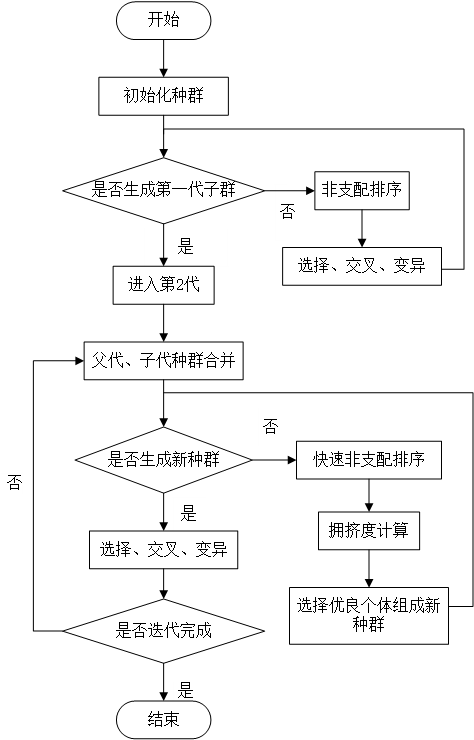
3.8 NSGA-II算法 16

第4章 算法仿真与分析 20

4.1 多目标优化问题 20

4.2 评价指标 20

4.3 仿真环境设置 21

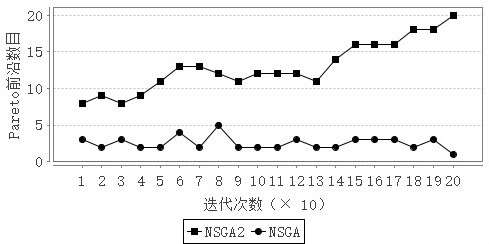
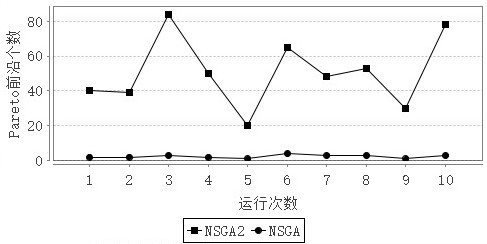
4.4 仿真结果与分析 22

第5章 总结与展望 26

5.1 论文总结 26

5.2 未来展望 26

参考文献 27

附录A 29

致 谢 49

第1章 绪论

1.1 研究目的及意义

科技的迅速发展使产品换代的速度加快，导致废弃产品日益增多^[1]，进而增加了对世界各国自然环境的压力；与此同时，随着人类社会文明的进步，环境污染、资源缺乏等问题日益严重，我们将更加关注经济的可持续发展和高质量发展而不是快速发展，可持续发展战略已经被全球越来越多的国家当作一项优先战略，在提高人类生活幸福指数的同时减少对自然资源的使用。可持续生产整合了生产和逆向生产，即闭环生产^[2]。回收寿命终结（end of life，EOL）产品不仅有效地防止了自然资源的快速消耗而且能够积极应对传统废弃产品处理方式带来的环境污染问题，使各类废弃产品带来额外的价值。废旧产品只有经过拆卸才能够实现回收再利用以解决资源和环境问题。因此，拆卸线平衡问题在国内外受到了广泛关注。

1.2 国内外研究现状

Askiner Gungor和Surendra M. Gupta首次提出DLBP时就针对因EOL产品存在缺陷导致拆卸任务失败的情况设计了拆卸线的平衡算法^[3]。在解决DLBP的早期研究过程中，主要采用启发式算法。虽然启发式算法原理简单，能够迅速求出可行解，但是由于产生的可行解完全依赖启发式规则，具有不确定性，因此并不能保证可行解的质量。McGovern和Gupta证明了拆卸线的平衡问题和装配线的平衡问题相似，都包含随机任务时间、不同的线布局以及同时考虑的冲突目标增加了其复杂性。进而McGovern和Gupta提出了组合优化技术，比如贪心算法与2-opt算法^[4]结合，该算法在处理危险和高需求零件的同时最小化了工作中心的数量。

然而，随着DLBP规模的不断扩张，可行解的数量以阶乘的形式增长。因此以上方法不适合解决大规模问题。多目标人工鱼群算法^[5]和多目标蚁群算法^[6,7]虽然能够得到针对不同特性的拆卸方案，但可行解的质量仍然需改进。

在解决多目标拆卸线平衡问题时，启发式方法和精确方法被DLBP的强约束性所约束，只适合求解小规模问题，虽然某些智能算法在建立数学模型阶段虽然考虑了多目标优化，但将多目标优化问题其转变为存在权重关系的单目标优化问题，比如字典排序，而多目标之间往往互相冲突，因此并不能保证所有目标之间的均衡性。

1.3 本文研究的主要内容

本文针对DLBP的强约束性，使用基于Pareto支配策略的NSGA与NSGA-II处理属于多目标优化问题的拆卸线平衡问题，得到最优的拆卸序列集合。本文共分为五章。

第一章简述了研究DLBP的目的、意义与国内外的研究现状，并在本节中介绍了本文的结构。

第二章介绍了DLBP的定义，建立了基于本文研究内容的数学模型。

第三章概述了遗传算法的基本原理，结合DLBP的数学模型对遗传算法中的变化算子进行了介绍，并阐述了Pareto支配的理论基础及NSGA算法与NSGA-II算法。

第四章结合DLBP介绍了多目标优化问题及其评价指标，使用NSGA与NSGA-II对DLBP进行了仿真，并使用评价指标评估算法的综合性能。

第五章总结了本文的研究内容，并对处理多目标优化问题的方向进行了展望。

第2章 拆卸线平衡问题定义及建模

2.1 问题描述

本文在充分考虑一个EOL产品在满足优先关系约束的条件下对该产品进行完全拆卸，目的是在最小化工作中心的开启数量和优化多个目标的同时，将EOL产品的拆卸任务分配至各工作中心得到最优拆卸序列。

由于EOL产品本身具有不确定性，因此拆卸线具有较高的复杂性^[8]。一方面，拆卸线工作中心的工作方式分为同步方式与异步方式。同步方式是指拆卸线工作中心的节拍时间一致，每个工作中心以相同的标准运行；异步方式是指拆卸线各工作中心的节拍时间不一致，各工作中心在完成当前拆卸任务后，若下游工作中心处于空闲状态则把该拆卸任务传递给下一个工作中心。由于异步方式更加适合拆卸线同时拆卸不同种类的寿命终结产品，而本文研究的是同一种类拆卸产品的拆卸情况，选择同步方式能够降低DLBP数学模型的复杂度进而使模型得以简化。

另一方面，线布局规定了工作中心处理拆卸任务的方法。在文献中，直线型布局、U型线布局和循环型布局是经常被采用的^[9]。直线型布局中，每个工作中心都被分配了一项拆卸任务，任务按照先后次序执行，如图2.1线布局所示；在U型线布局中，拆卸线的入口与出口在同一个地方，工作人员站在拆卸线中间在同步方式的情况下，来对多个工作中心的拆卸任务进行拆卸，基于此，U型线布局通常是手动的，如图2.2所示。在循环型布局中，拆卸线呈现为一个环状结构，工作中心被安装在环形拆卸线的周围，如图2.3所示。由于U型线布局通常是手动的，且本文所拆卸的EOL产品的部件较多，若采用循环型布局，厂家建造拆卸线所需要的成本过多，同时直线型布局更符合自动化方式，因此在本文中，拆卸线采用直线型布局。

图2.1 基本直线型布局

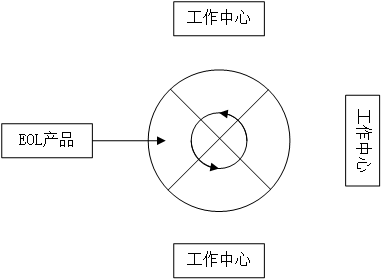图2.2 U型线布局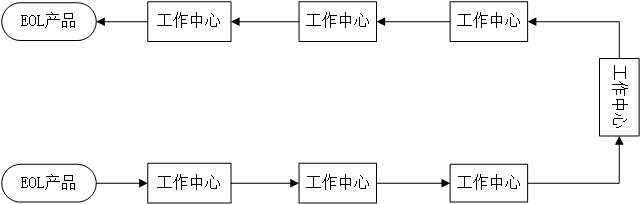

图2.3 循环型布局

实际DLBP具有许多的任务属性，比如拆卸时间、处理成本和拆卸成功的可能性等属性。其中，拆卸时间是首要属性，拆卸成功的可能性是次要属性。由于每个工作中心只在规定的时间内执行拆卸任务，且工作中心拆除的任务是随机的，为了保证开启工作中心的数量能够尽可能少，因此决定工作中心作业时间的节拍时间尤为重要。

为了直观的描述优先关系约束，本文使用优先图来表示拆卸EOL产品时的优先关系^[10]。一个只有10项拆卸任务的EOL产品的优先关系约束图如图2.4所示，两个拆卸任务之间的优先关系约束使用带有方向性的实线连接。从图中可以看出，任务8与任务2需要在拆卸任务3之前拆卸才能够保证拆卸过程能够顺利进行，从该优先关系约束图中可以得到的某个可行的拆卸序列为。

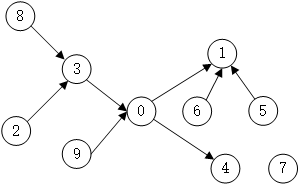图2.4 优先关系约束示意图

为了降低数学模型的复杂度，做出的假设如下：

1. 对EOL产品完全拆卸；
2. 被拆卸产品没有升级或改造；
3. EOL产品足够多；
4. 工作中心以同步方式工作，节拍时间已知；
5. 每项拆卸任务的拆卸时间已知；
6. 拆卸线采用直线型布局。

2.2 数学模型

本文中建立的DLBP数学模型如下：

（2.1）

（2.2）

（2.3）

（2.4）

（2.5）

上式中，为工作中心数目；为寿命终结产品包含的零件数目；为节拍时间（Cycle Time，CT）；为变量，若任务被分配到工作中心，则，否则；为变量，若任务具有危害性，则，否则；是任务在拆卸序列中的位置；若任务是任务的紧前任务，则，否则。式（2.1）是第一个目标函数，目的为最小化工作中心的开启数量以减少成本和节约资源；式（2.2）是第二个目标函数，目的是最小化拆卸过程中的危害性，若某个零件具有危害，则该零件应尽可能被安排在拆卸序列中靠前的位置，在拆卸过程中较早拆卸，使的值尽可能小；式（2.3）是任务分配约束，它确保每个拆卸任务不能被同时分配至多个工作中心；式（2.4）是优先关系约束，代表任务必须在任务之前执行；式（2.5）是节拍时间约束，表示工作中心的作业时间不超过节拍时间。

第3章 基于GA的算法设计

3.1 遗传算法的基本原理

在遗传算法（Genetic Algorithm，GA）中，每条染色体都象征着一种潜在的解决方案，但由于某些问题模型本身对于可行解决方案有限制，需要对每个解决方案进行约束修复，以构成最初始的可行解决方案。每一代种群都是由一定数量的个体构成，每个个体实际上是经过基因编码的染色体。如图3.1所示，在保证初代种群的所有个体均为可行解的前提下，遗传算法开始高效、并行的优化，并逐代进化出逼近理想解的最优解，每一代个体根据适应度的大小选择当代中的最优个体优先进入下一代种群，确保进化过程中的最优个体不丢失。 GA避免了传统算法对目标函数求导的过程，避开了优化函数的连续性约束条件；与此同时，交叉、变异操作可以使当代种群产生的新个体共同参与进化过程，保证了每代种群的稳定性与多样性，有效的防止种群的早熟，增大了GA的灵活性。在末代种群中的最优个体被解码后，生成了该问题模型的最优解。

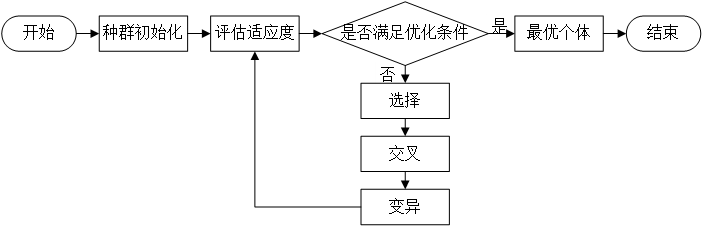GA为解决复杂系统面临的不依赖领域和类型的优化问题提供了一个通用的框架，具有良好的全局优化能力，虽然需要针对实际问题模型进行优化，但实际问题的算法通常可通过如3.1所示的步骤构造遗传算法来解决问题。

图3.1 遗传算法流程图

3.2 编码与解码方法

根据3.1节可知，每条染色体代表一种潜在的解决方案，因此如何编码完成种群初始化不仅是基于遗传算法的拆卸线平衡问题的关键，此外，它影响了GA中交叉算子与变异算子的实现方法。

3.2.1 编码

本文中，每条染色体代表一个可行的拆卸序列，拆卸序列也被称作为拆卸树（disassembly tree，DT），即任务与工作中心间的分配关系。由于编码方法直接影响交叉算子与变异算子的效率^[11]，本文采用基于零件编号的实数编码方式，即按照EOL产品中个零件分配至工作中心的先后顺序，将拆卸任务排成一行，每个基因对应一项拆卸任务^[12]。为了防止种群在迭代过程中发生无意义的进化，产生不可行解或非法解，需确保以下两点：

1. 种群初始化过程期间生成的所有产生个体均为可行解，即需要检查每个生成的个体的优先关系约束。若某个解为不可行解，则需要根据式（2.4）将其纠正为可行解；
2. 经过遗传算子的操作后，个体可能会由可行解转变为非可行解，此时需要对该个体进行修复。修复算法的细节将在3.5.3节中说明。

本文中，EOL产品中的零件使用从0开始的实数编码，使用“-1”分隔不同的工作中心。因此从每条染色体上可以方便的得出开启工作中心的数量、某个工作中心的任务集合、此DT的危害指数以及任务集合是否超出节拍时间，以检查其可行性。由于拆卸不同的任务所需的时间可能不同，因此不同工作中心中的拆卸任务数量也可能不同，使开启工作中心的数量有差别，导致了染色体的长度并不是固定不变的。若一个EOL产品包含N个零件共有项拆卸任务，假设每个工作中心因周期时间约束只能拆卸一个零件，则染色体的最大长度为。如图3.2所示，此染色体表明该EOL产品共有10项拆卸任务，用表示。编码的排列顺序表示拆卸任务被分配至工作中心的先后次序，其中第一次分配拆卸任务4，第二次分配拆卸任务9，以此类推。

图3.2 编码后的染色体

3.2.2 解码

解码是指将拆卸序列恢复为任务分配方案，即根据式（2.5）的约束规则将所有的拆卸任务分配至工作中心^[13]。例如，在图3.2中，该染色体显示拆卸这个EOL产品共需要3个工作中心，每个工作中心分别有3个、5个和2个拆卸任务，第一个工作中心处理任务4、9和6，第二个工作中心处理任务2、5、0、8和1，第三个工作中心处理任务7和3。

3.3 种群的初始化

种群的初始化即随机生成个不同的个体，每个个体都由一条染色体组成。初始化种群的目的是快速获得与约束关系相关的可行解。EOL产品中各零件在式（2.3）与式（2.4）的约束下构造可行解。

3.4 适应度函数

本文中，使用多目标函数的加权和组成一个标量适应度函数，权重值在进化过程中随机确定^[14]。在GA迭代初期，通常会产生一些竞争力强、适应性良好的个体，它们影响了算法的选择算子，降低了GA的全局优化性能；由于遗传算法随着迭代次数的增加会使可行解逐渐逼近最优解，因此在进化末期会导致个体在进化过程中遗传算法不能跳出局部最优点，出现丢失问题模型最优解的问题。同时，由于不同目标函数的度量单位不同，需要对目标函数进行尺度变换，即归一化处理，如下式所示。

（3.1）

式（3.1）中，与是第个目标函数的最大值与最小值，是第个个体的目标函数值，为归一化后的目标函数值。

结合每个目标函数值，通过以下公式得到个体的适应度函数：

（3.2）

式（3.2）中，是非负常数，且。权重值由下式计算得出：

（3.3）

式（3.3）中，是非负常数。

由于本文的只有两个目标函数，也就是，因此，可简化权重值的计算，即下式所示：

（3.4）

（3.5）

3.5 变化算子

3.5.1 交叉算子

本文的交叉方式选择单点交叉，种群中随机配对的染色体根据交叉概率判断是否进行交叉。如图3.3所示，两个随机配对的染色体，随机选择的交叉点是8，即选择的拆卸任务是任务8，两个父代染色体分别被交叉点分成左右两个部分，交换父代染色体1与父代染色体2在拆卸任务8后面的所有的拆卸任务，得到两个后代染色体。

图3.3 交叉操作

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：