英语原文共 12 页，剩余内容已隐藏，支付完成后下载完整资料

---

钢筋混凝土结构

B.PARK and T.PAULAY

4

受弯构件的强度

4.4截面双向弯曲

钢筋混凝土梁有时会受到导致双轴(不对称的)弯曲的载荷，例如，一个独立的梁支撑的墙暴露在风压下可能会接受水平和垂直的载荷。双轴弯曲截面如图4.16所示。

图4.16. 具有双轴弯矩的钢筋混凝土梁截面

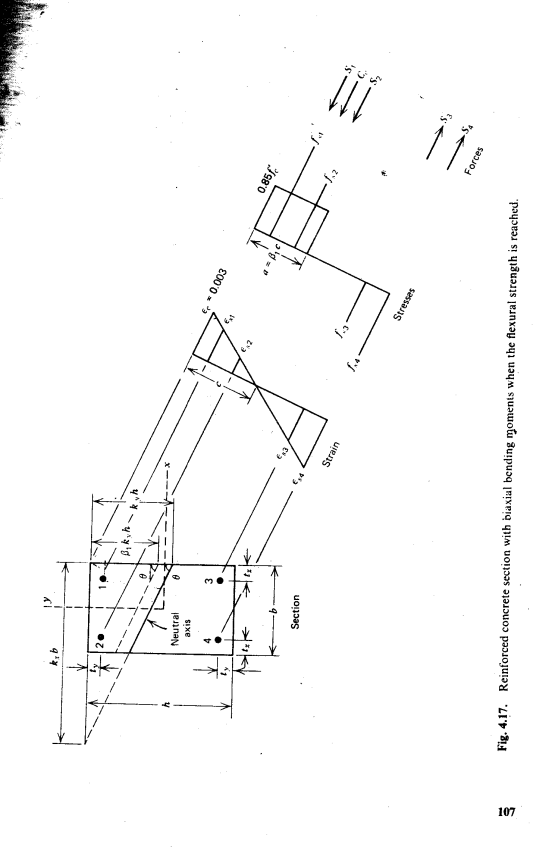
达到抗弯强度时的截面如图 4.17.所示。该截面将假定由编号为1,2,3和4的四根钢筋进行加固，如图4.17.所示。钢筋较多的截面可以用下面的方程进行分析。把这些小节分成四组。其中 1,2,3和4是中心体。可以用计算机程序，或者是可以使用以下截面方程的扩展，来分析沿四个面分布钢筋的截面,或者考虑任意位置的单个钢筋。

在具有双轴弯曲的截面中，中性轴向水平方向倾斜，倾斜程度取决于两个方向弯矩的比例和截面特性。假设等效应力块的深度为beta;1，乘以中性轴深度，平均应力为0.85。这个等效应力块与实际应力块并不完全等效(见3.4节)，但对于以设计为目的来说，它足够精确。

中轴

区间

力

压力

应变

对于给定的截面，其抗弯强度如下:

1. 考虑图4.17的应变图的类似三角形，可以发现钢中的应变:

there4; （4.64）

同样的，还有

（4.65）

（4.66）

（4.67）

其中，正应变表示压缩。

1. 钢的应力和力遵循钢的应力-应变曲线。对于定义明确的观察点的通常情况，对于块1，如果

,

或者如果

, (4.68)

或者如果

,

第2，3和4小节的应力也得到类似的结果。

钢的力是由以下产生的

(4.69) (4.70)

(4.71) (4.72)

3.混凝土中的合力及其位置将取决于等效压应力块的形状和面积。四种可能的形状如图4.18所示。

对于情形一

(4.73)

(4.74)

(4.75)

例

例

例

例

等效压应力块面积

图4.18. 可能形状的等效压应力块面积

同样的，可以在和中找到表达式，对于例2、3和4，由Mattock.Kriz和Hognestad ^4.7给出。

平衡时，中性轴的位置必须使纵向力的总数为0

（4.76）

5.在具有抗弯强度的轴上作用的构件，可以通过取关于X方向轴(如截面的底部边缘)和Y方向轴(如截面的左侧边缘)的内力力矩来找到。

（4.77）

（4.78）

当使用这些表达式时，应将适当的符号(正的表示压缩，负的表示张力)代入方程式4.76至4.78。

具有双轴弯矩的截面的分析和设计都是困难的，因为需要试验和调整程序来找到中性轴的倾角和深度。

例4.9

混凝土梁有一个10英寸(254毫米)的正方形截面，由4根9号钢筋(直径28.7毫米)，在截面的每个角落放置一根钢筋。从每根棒材的质心到截面的相邻边的距离为2英寸(50.8mm)。这种钢的明确屈服强度为40000psi(276 N/mm2)，弹性模量为29times;10⁶psi(0.2times;10⁶N/mm²)。混凝土的圆柱体强度4000psi(27.6 N/mm²)。计算截面的抗弯强度，如果它受到的双向弯矩等大小的轴平行于边缘。

解决方案

由于截面为方形，双轴弯矩相等，混凝土受压面积呈等腰三角形(k_X=k_y=k);因此，中立轴的倾斜度是已知的。图4.19显示了该部分。用一个试验和调整步骤来找到中立轴深度。

首先估计

对于图4.19中的中立轴位置，设k=0.70。从公式4.64写到4.67

也有 因此由方程式4.86得

psi

psi

由方程式4.69到4.72可得

lb lb lb

外部作用

力

张力

截面

图4.19. 例9的截面和内部、外部作用

由公式4.73得出

lb

there4;lb

因此，拉力太多，提高K值。

第二种估计

设K=0.8.然后使用之前的方程式，

there4;psi psi

psi

there4;lb lb lb

lb

there4;lb

因此，压力太多，减少K。

第三种估计

线性插值，使用从平衡方程先前剩余的力

使用前面的平衡方程，

there4;psi psi

psi

there4;lb lb lb

lb

there4;lb

因此，平衡方程是可以的。

从方程式4.74和4.75可得

in

从方程式4.77和4.78可得

=65,450（10-2.07） （39,320-32,190）（10-2）

（-32,190-40000）2

=431,700lb·in（48.7KN·M）

或者，作用于对角线的合力弯矩为

lb·in(68.9KN·m)

值得注意的是，仅绕X或Y方向弯曲的截面的抗弯强度可计算为547,600lb·in(61.8KN·M)

很明显，手算一般双轴弯矩方程需要费力的计算，因为为找到给定值和的中性轴的深度和倾角需要试验和调整程序。然而，这些方程可以用数字计算机编制程序。图4.20所示为各弯矩和组合的相互作用曲线，它将使截面各角钢含量相等的截面达到抗弯强度。以这种形式绘制的设计图表将能够找到特定组合的钢材区域和。图4.20中曲线的形状随的增加而变化。其中，是总钢面积除以混凝土面积。作为一个近似指标，如果给定截面的和已知，直线和曲线将总是保守相互作用；但圆形曲线(如果两个方向的单轴抗弯强度不同，则为椭圆形)可能是不安稳的，特别是在高的值的时候。

增长

在受弯强度下具有双轴弯矩的钢筋混凝土截面相互作用曲线的形式

4.5梁的横向失稳

当采用细长梁时，在强度发展之前的失稳可能是导致破坏的原因。失稳破坏表现为伴随扭转的侧向屈曲，如图4.21所示。这种不稳定性可以是重要的情况下，如果受弯平面的受弯刚度比其侧刚度大得多，梁缺乏横向支持。这个问题相当罕见，因为大多数设计师会直觉地选择紧凑的部分。在预制混凝土结构的安装过程中，在对构件提供足够的侧向约束之前，可能会出现这种危急情况。

图4.21 梁的横向失稳

如果试图真实地评估钢筋混凝土行为的所有特征，这个问题的分析处理就变得复杂起来。由于没有足够的实验证据证明理论推导出的临界载荷可以令人信服，这里没有尝试量化相关参数。这只能通过使用有争议的假设来实现。

米歇尔经典解^4.8在关键时刻线性弹性中产生不稳定性。同类的，各向同性棱柱梁为

（4.79）

公式中，当i=随荷载类型变化的系数，取值如下：

1. n表示沿梁的等力矩
2. 均布荷载3.53

（e） 中心点负荷4.24

=混凝土弹性模量

=混凝土刚性模量

=混凝土截面的主要和次要轴的惯性矩

=混凝土截面的等效极惯性矩

=梁的无支撑长度

=在截面的质心以上施加荷载的点的距离

Marshall^4.9已经调查了这些参数的适用性与钢筋混凝土，并试图建立的限制，真正的关键时刻可能会发生。单个量的变化是非常大的，根据这一特性，方程式4.79的一些简化应该是正常的。对横向屈曲敏感的截面有至少为2的深宽比。因此，如果也考虑开裂的影响，则比值会变得很小，可以取为零。有了这些简化步骤，方程式4.79变为

(4.80)

在对临界弯矩进行评价时，必须考虑到混凝土在受压过程中是非线性的;因此，在高应力时，需要考虑弹性模量的减少。在对惯性矩的评估中，必须考虑到弯曲开裂的影响。这种开裂将沿着梁根据弯矩模式变化。的计算可以仅根据受压区的混凝土截面部分。刚性模量的值与有关。但混凝土和腹板钢筋对扭转刚度的相对作用是不确定的。其他不确定性是:混凝土截面的数量，应包括在内的估算的等效极矩惯性，以及双轴弯曲影响扭转的程度。显然，要准确计算刚度项是困难的。

将代入，非线性范围内的弹性模量用圆柱体抗压强度表示，、、用截面尺寸表示，柱状矩形梁的临界弯矩方程近似为

（4.81）

其中为数值常数，为截面宽度，为受拉钢的有效深度。

当发生失稳破坏时，梁的受弯承载力将大于临界弯矩。然而，受弯能力取决于钢含量，并且对于一个单独加固的部分，这个值是受到相似限制的

（4.82）

当，，和（1psi=0.00689N/MM²）。

钢筋不足的梁在屈曲方面可能不是关键的。因此，考虑可用钢量最大的梁时，临界条件近似为

or （4.83）

当。

通过对变量方程式4.80做极限假设^4.9，值在均布荷载梁的宽极限100和580范围内。考虑这些限制，进一步完善分析，考虑到弯曲钢的贡献，^4.10是不对的。

Marshall^4.9通过分析现有数据发现，的值越大越接近正确。应该指出的是，传统上使用的单独跨宽比，，不能充分描述梁的失稳准则.

当考虑蠕变的影响和可能的初始失稳，并注意到失稳破坏表现出有限的延性时，我们意识到设计中使用的能力折减系数必须是小的值。^4.9另外，所规定的极限几何参数也应刻意保守一点。为防止横向失稳，英国规范CP110^4.11采用了以下限制:

1. 对于简支梁或连续梁，横向约束之间的清晰距离应该是这样的

和 （4.84a）

1. 对于仅在支座处有横向约束的悬臂，其值应为

和 （4.84b）

如果超过这些限制，临界弯矩将支配梁的强度。使用Marshall的估计^4.9,这个的近似值是

(4.85)

建议采用容量还原系数。

4.6参考资料

4.1 C. S. Whitney,'Design of Reinforced Concrete M

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[262098]，资料为PDF文档或Word文档，PDF文档可免费转换为Word