基于卡尔曼分布式状态估计的机艇协同巡航编队的研究毕业论文
2020-02-19 07:51:01
摘 要
多体系统具有强大的群体能力,由无人机和无人艇所组成的异构多体系统,不论在民用或是军用领域均具有极大的应用价值。编队控制作为协同控制中的一个重点问题,具有广阔的研究前景和极高的研究价值;卡尔曼滤波作为一种经典的滤波算法,具有广泛的应用空间。本文主要研究了机艇协同中的编队控制问题,同时引入分布式卡尔曼滤波来进行信息状态的测量估计。该研究首先探讨了无人机和无人艇的动力学模型及路径跟踪算法、编队控制算法和分布式卡尔曼滤波算法,并通过仿真验证理论正确性。最后整合上述内容,完成系统设计,用仿真实验测试了系统的性能,仿真结果表明,该系统具有良好的编队效果和较高的稳定性、准确性。
关键词:多体系统;机艇协同;编队;分布式卡尔曼滤波
Abstract
Multi-Agent systems can demonstrate strong group capabilities, and heterogeneous multi- agent systems consisting of UAV and USV have great application value in both civil and military fields. As a key issue in coordination control, formation control has broad research prospects and high research value. On the other hand, as a classical filtering algorithm, Kalman filtering has a wide application space. This paper mainly studies the formation problem under the UAV-USV coordination, and introduces distributed Kalman filter to measure and estimate information. In this paper, the dynamics model and path tracking algorithm of UAV and USV, formation algorithm and distributed Kalman filter are studied respectively, and the theoretical correctness is verified by simulation. Finally, through the system design, the above content is integrated, and the feasibility and performance of the system are verified by simulation experiments. The simulation results show that the system has good control effect.
Key Words:multi-agent systems;UAV-USV coordination;formation;Distributed
Kalman Filter
目 录
第1章 绪论 1
1.1 研究工作的背景与意义 1
1.2 国内外研究现状 1
1.3 课题研究内容、预期目标 2
1.3.1 课题研究内容 2
1.3.2 课题预期目标 2
1.4 本论文的结构安排 2
第2章 多体系统一致性的基本原理 3
2.1 数学原理 3
2.2 仿真实验及分析 4
第3章 无人机的运动建模及路径跟踪算法 5
3.1 动力学建模 5
3.2 路径跟踪算法 7
3.3仿真实验及结果分析 8
3.3.1 仿真参数及仿真目标 8
3.3.2 仿真结果与分析 9
第4章 无人艇的运动建模及路径跟踪算法 12
4.1 动力学建模 12
4.2 路径跟踪算法 13
4.3 仿真实验及结果分析 15
4.3.1 仿真参数及仿真目标 15
4.3.2 仿真结果与分析 16
第5章 编队控制算法 20
5.1 数学原理 20
5.2 仿真实验与结果分析 20
第6章 分布式卡尔曼滤波器 22
6.1 数学原理 22
6.2 伪代码形式 24
6.3 仿真实验与结果分析 24
第7章 系统设计及仿真实验 28
7.1 系统设计 28
7.2 仿真实验与结果分析 29
7.2.1 仿真参数及仿真目标 29
7.2.2 仿真结果及分析 29
第8章 结论 32
8.1 全文总结 32
8.2 研究展望 32
参考文献 33
致谢 35
第1章 绪论
1.1 研究工作的背景与意义
长期以来,群体行为所展示出的智能化令科研人员着迷:由多个简单单一个体组成的群体,通过简单的规则,却可以展现出非凡的智能化程度。群体所展现出的能力往往具有的效果,即由单一简单个体所组成的多体系统(多体系统是指多个航行体在给定的环境中移动并共同完成给定任务的系统[1]),具备更强的鲁棒性,更好的容错性和更高的智能化程度。如相对单一个体,多体系统增加了空间覆盖面、时间吞吐量并提高了作业效率[2],且对解决复杂任务具有良好的效果[3],目前已在多种领域得到应用[4-6]。因此多体系统在民事、军事等多个领域有广阔的应用前景和极高的研究价值。根据群体中航行体是否具有相同的状态维度,多体系统可分为同构多体系统和异构多体系统[7]。目前有关同构多体系统的研究较为丰富,而实际应用中,往往由多种航行体来共同执行任务,即为异构多体系统。
一方面,无人艇和无人机不论在民用或军用领域均具有极大的应用价值,而本文所研究的基于无人机-无人艇的异构多体系统,可以融合二者各自的优势(无人机具有较快的移动速度及较远的作战半径的优势,无人艇具有功能多样、可执行多种任务的优势),以执行更加复杂、困难的作业任务。
另一方面,分布式状态估计是协同控制中的重点问题,其主要通过对其他航行体(如领导者)的状态进行估计来使多体系统达到一致;同时多体系统中的编队控制可以有效提高多体系统执行任务时的避碰能力和行动效率,使多体系统更加有效地完成指定的任务。
综上,无人机-无人艇的分布式状态估计及编队巡航的研究,对机艇协同的研究进展和实际应用具有重要的推进意义。
1.2 国内外研究现状
目前国内外针对同构多体系统一致性问题的研究较为全面,而针对异构系统一致性问题的相关研究较少。由于实际中的多体系统多为异构多体系统,因此异构多体系统有更大的应用空间和应用价值。
在多体系统的一致性问题研究中,由于异构多体系统中航行体具有不同的状态维度,因此状态一致性研究没有意义,而我们更多地关注输出一致性问题。针对异构多体系统的输出一致性问题,大致有以下三种方法:(1)利用分布式状态估计来获得领导者的状态,再根据输出方程到达输出一致性[8];(2)基于ρ-copy内膜理论达到输出一致性;(3)利用通信网络的传输信息实现输出一致性。
1.3 课题研究内容、预期目标
1.3.1 课题研究内容
首先了解多体系统中一致性的基本知识,掌握多体系统一致性的基本定理及算法;学习并理解无人机、无人艇的相关背景和知识,分别掌握有关无人机和无人艇的运动学模型,并分别为其设计路径跟踪算法;熟悉跟随领航者法的编队控制算法;了解卡尔曼滤波的知识,并应用分布式卡尔曼滤波算法,设计无人机-无人艇异构多体系统的分布式状态估计器;引入无人机、无人艇的运动学模型和路径跟踪算法,通过分布式卡尔曼滤波来估计无人机、无人艇状态,实现系统编队控制,完成机艇协同巡航编队的研究。
1.3.2 课题预期目标
1、学习并掌握上述基本内容中的相关理论知识;2、通过数值仿真实验,分别验证一致性的基础算法、无人机的动力学模型及路径跟踪算法、无人艇的动力学模型及路径跟踪算法、几何编队算法和分布式卡尔曼滤波的理论推导验证;3、整合上述的几部分,搭建仿真平台,完成系统设计;4、根据实验结果修改调整模型,完成仿真验证。
1.4 本论文的结构安排
本文的结构安排如下:
第一章阐述了本文研究工作的背景、意义和相关的国内外的研究现状,叙述了课题研究内容和预期。
第二章介绍了一致性算法的原理和连续时间、离散时间的基本算法,通过仿真实验测试了一致性算法的效果。
第三章介绍了无人机的应用背景,引入无人机动力学模型,并研究了其路径跟踪算法的原理。然后将无人机的动力学模型放入路径跟踪算法之中,通过仿真实验验证了无人机动力学模型的可行性和路径跟踪算法的优良性能。
第四章介绍了无人艇的背景,引入了无人艇动力学模型,分析其路径跟踪算法的原理,并用改进的PID控制器实现路径跟踪算法。然后将无人艇的动力学模型放入路径跟踪算法之中,通过仿真实验验证了无人艇动力学模型的可行性和路径跟踪算法的优良性能。
第五章介绍了两种基于几何变换的编队算法,通过仿真实验验证了其效果。
第六章介绍了卡尔曼滤波和分布式卡尔曼滤波的原理,并设计了仿真实验,对比了两种滤波算法性能上的差异,并验证了分布式卡尔曼滤波应用于编队控制的可行性。
第七章整合3-6章的内容,设计了基于卡尔曼分布式状态估计的机艇协同巡航编队,并搭建了仿真平台,通过仿真验证了系统的可行性及其性能。
第八章对该研究进行总结,并提出了研究展望。
第2章 多体系统一致性的基本原理
信息一致性问题就是通过信息共享,航行体群就关键信息达成一致,从而保证他们可以协同作业。解决一致性问题需要设计合理的分布式算法,从而保证航行体集群即使在非理想的条件下(如通信范围受限、通信拓扑时变等),也可以达到信息一致。
2.1 数学原理
当多个航行体对设定的变量取值达到共识时,就称达到“一致”。为了达到信息一致性,必须存在一个各航行体共同关心的变量,称为信息状态。一致性算法可以定义为:各航行体之间的相互协商,使信息状态达成一致的算法。一致性算法的基本思想是对每个航行体的信息状态赋予相似的动力学特性[9]。
假设在编队中有个航行体,编队的通信拓扑可以用有向图表示,其中表示节点集,表示边集。一个基本的连续时间的一致性算法为:
式(2.1)中,表示第个航行体的信息状态,表示有向图的邻接矩阵的第项,的值代表第个航行体对第个航行体的信息的接受程度(权重),表示完全不接受对方的信息,表示完全接受对方的信息。如果整个多体系统的通信拓扑和邻接矩阵是时不变的,那么当各个航行体信息状态达到一致时,其值为所有航行体的初始信息状态的线性组合。将式(2.1)改写成矩阵形式:
式(2.2)中,表示信息状态,表示与图相关的非对称拉普拉斯矩阵,即对于。对于任意的和所有,当时,,则称达到一致。
一个基本的离散时间的一致性算法为:
式(2.3)中,表示行随机矩阵在离散时刻的第项。当一个非负方阵的各行元素之和均为1时,称该方阵为行随机矩阵。这里的和的数值具有相同的表示含义。式(2.3)的矩阵形式为:
对于任意的和所有,当时,若,则称达到一致。
2.2 仿真实验及分析
参考式(2.4),设计了一个数值仿真实验,验证基本的一致性算法。
令航行体的数目,随机生成初始状态,并随机生成一个随机邻接矩阵(其每一行的和为0):
设置仿真步长为0.001。多航行体信息状态趋于一致的过程图如图2.1所示。
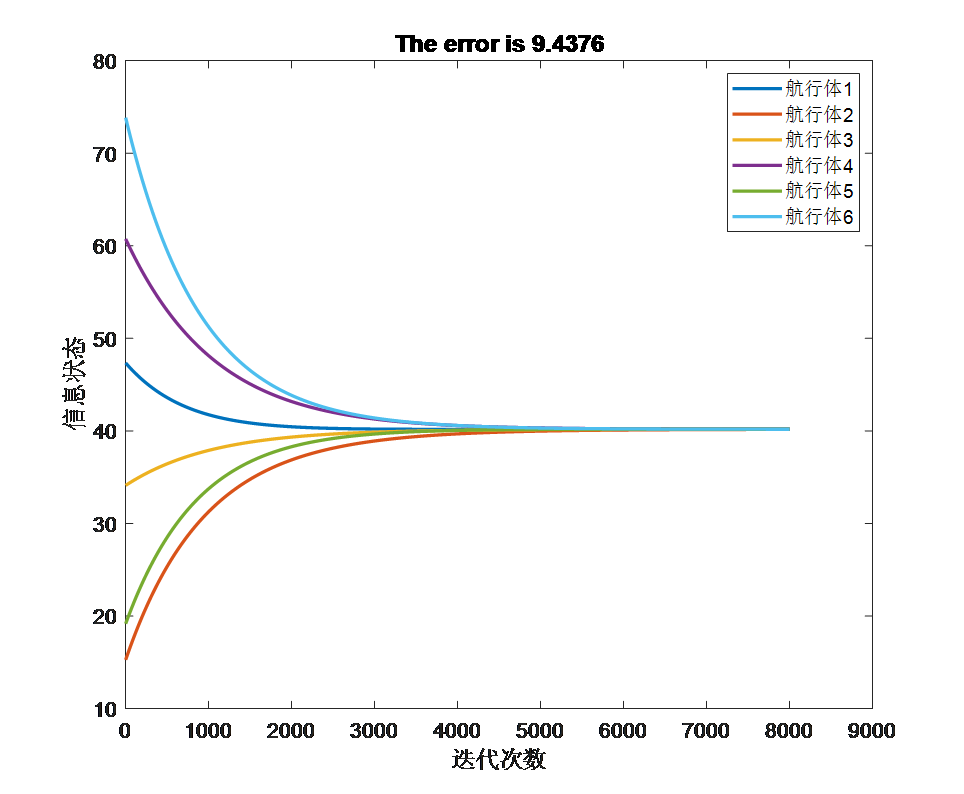
图2.1 信息状态趋于一致的过程图
第3章 无人机的运动建模及路径跟踪算法
无人飞行载具(Unmanned Aerial Vehicle, UAV),或称无人飞机系统(Unmanned Aircraft System,UAS),通常称为无人机。无人飞行载具是指通过遥控或者自动驾驶技术,进行科学观测及侦查等任务的飞行载具。无人机无论在民用或者军用领域均有很大的应用空间和价值[10]。与单架无人机相比,无人机集群在团队协作时具有更高的效率和操作灵活性,而实现无人机集群的协同控制的前提则是通过信息共享,集群达到信息一致性。目前,在军用无人机领域,蜂群战术已成为主流,其可以完成侦察、战斗和物流等任务;而在民用领域,多无人机的协同控制也具有巨大的应用空间,如物资投放、灾害应对和遥感测绘等。

图3.1 美国国土安全部的无人飞行载具
本章首先介绍无人机的数学模型,再介绍并实现无人机的路径跟踪算法[11],最后通过设计仿真实验并进行结果分析来验证无人机动力学模型和路径跟踪算法的可行性。本章主要借鉴了Taeyoung Lee等人整定的无人机数学模型及路径跟踪算法[12]。
3.1 动力学建模
简化后的四旋翼无人机动力学模型示意图如图3.2所示,,为惯性参考系,即,,其中的方向与重力加速度的方向相同。,为无人机的随体坐标系的轴向,其指向如图3.2所示。该四旋翼无人机包含4个独立的推进器,分别产生和的推力,这里将四旋翼无人机简化为刚体处理,则4个推进器处于同一个平面内。假每个推进器都是单独控制的,同时当第1、3个推进器顺时针旋转时,其产生方向为的推力,当第2、4个推进器逆时针旋转时,其产生方向为的推力。因此,可以将其合成为总推力,其方向为,位于四旋翼无人机的几何中心(同时也是质心)。为旋转矩阵,,其中为特殊正交群(the special orthogonal group,简称),满足以下性质:。为四旋翼无人机在惯性坐标系中的位置向量。
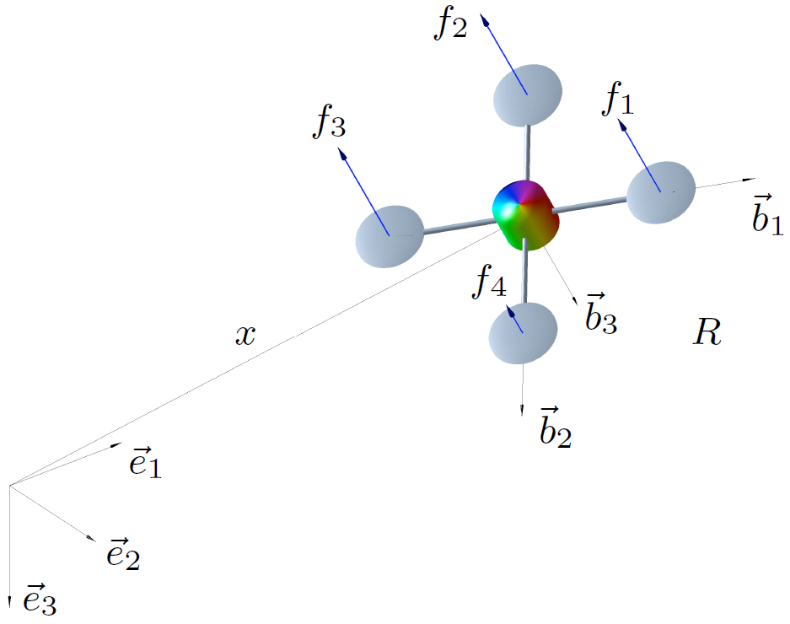
图3.2 四旋翼无人机动力学模型示意图
根据的定义和上述的假设,得到在惯性参考系中的总推力向量。假设推进器的扭矩与其产生的推力成正比,则以为参考,第个推进器产生的扭矩为,式中为扭矩常数。
基于上述假设,可以得到以无人机随体坐标系为参考系的力矩向量:
式(3.1)中,为四旋翼无人机推进器到其几何中心(同时也为质心)的距离。由于式(3.1)中矩阵的行列式为,因此当且时,该矩阵可逆,从而可以通过来求出。因此,可以将等价为控制输入变量。
四旋翼无人机的动力学方程为:
上式中,为以惯性坐标系为参考系的无人机速度向量;为无人机的总质量;为引力常量;为以无人机随体坐标系为参考系的角速度向量;为以无人机随体坐标系为参考系的惯性向量。
式(3.4)中,符号表示从到的映射:
式(3.6)中,。而为其逆映射,表示从到的映射。
3.2 路径跟踪算法
由上述论述中可知,四旋翼无人机的四个推进器转矩为四个控制输入变量,根据自动控制原理,最多可以实现对四个输出变量的渐进跟踪。又由于四旋翼无人机具有三个平动自由度和三个旋转自由度,因此不可能同时实现四旋翼无人机的位置和姿态的控制。
由于本文主要研究机艇协同巡航编队,因此这里选择四旋翼无人机的位置和作为控制变量进行控制。
下面介绍路径跟踪算法的数学原理:
令表示无人机期望的位置向量,则其位置误差和速度误差分别为:
同样,无人机的姿态误差和角速度误差分别为:
其中,计算出的无人机姿态矩阵和计算出的无人机角速度向量分别为:
通过式(3.12)得到,再通过从到的映射得到。式(3.11)中分别为计算出的和,同时由于,因此:
式(3.11)、(3.13)中分别为:
式(3.14)中,为期望的。令平面垂直于,则为在平面上的投影。式(3.15)中,和分别为位置误差和速度误差的系数。
最终,可以得到四旋翼无人机非线性控制器的输出和为:
式(3.17)中,和分别为姿态误差和角速度误差的系数。四旋翼无人机非线性控制器的结构图如图3.3所示。
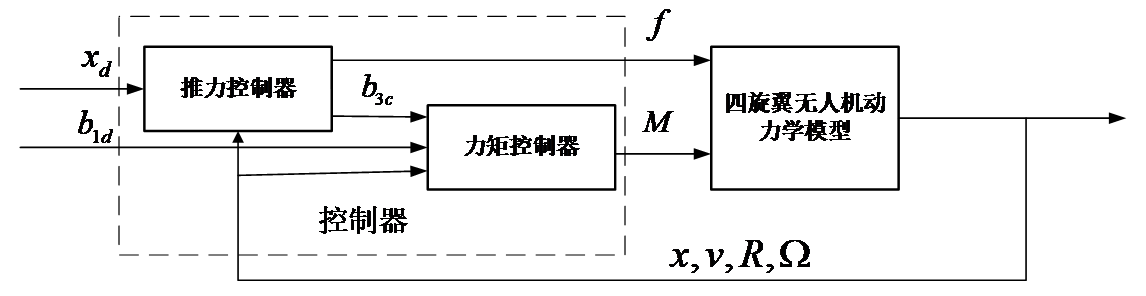
图3.3 四旋翼无人机的非线性控制器的结构图
3.3仿真实验及结果分析
通过MATLAB进行数值仿真实验,验证四旋翼无人机的动力学方程和路径跟踪算法。为了验证算法的响应速度和跟踪误差,本文设计了两种仿真实验:一种为静态靶单点定位,另一种为动态靶路径跟踪。
3.3.1 仿真参数及仿真目标
设置四旋翼无人机动力学模型的参数为:
设置控制器的参数为:
设置四旋翼无人机的初始状态为:
设置静态靶单点定位仿真实验的仿真目标为:
设置动态靶路径跟踪仿真实验的仿真目标为:
3.3.2 仿真结果与分析
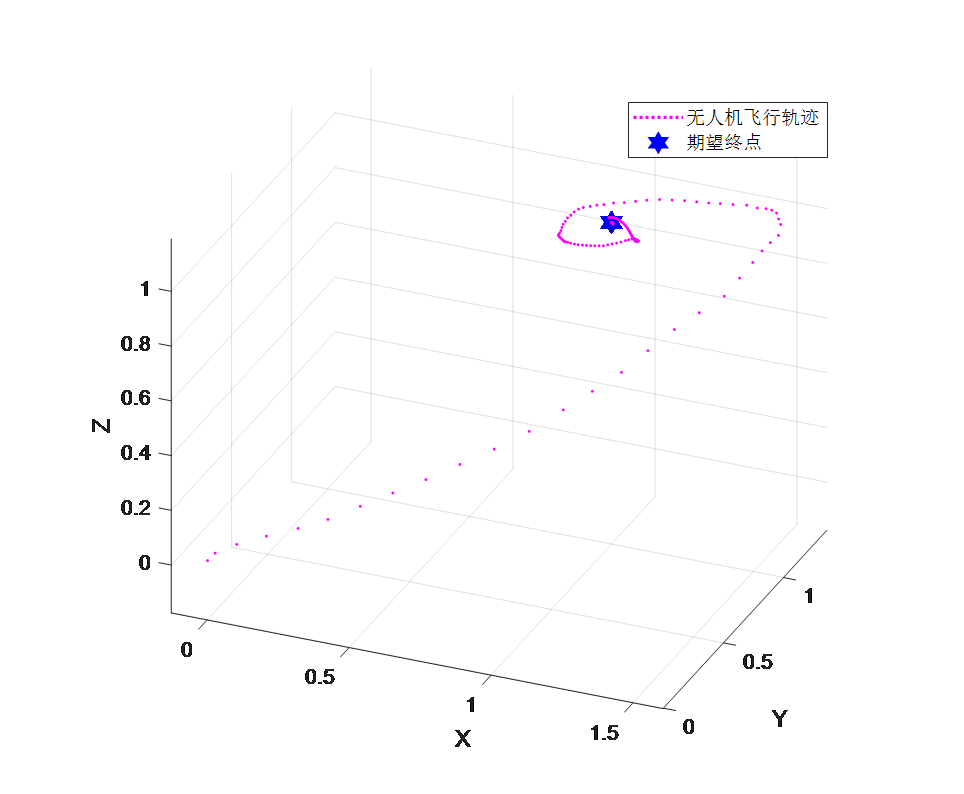
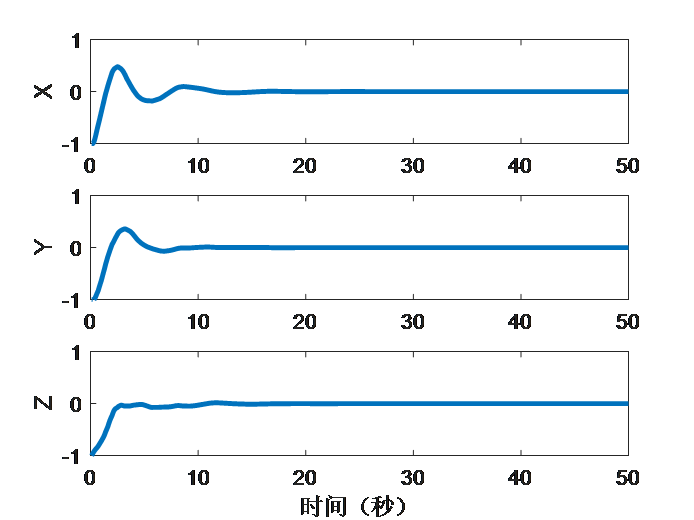
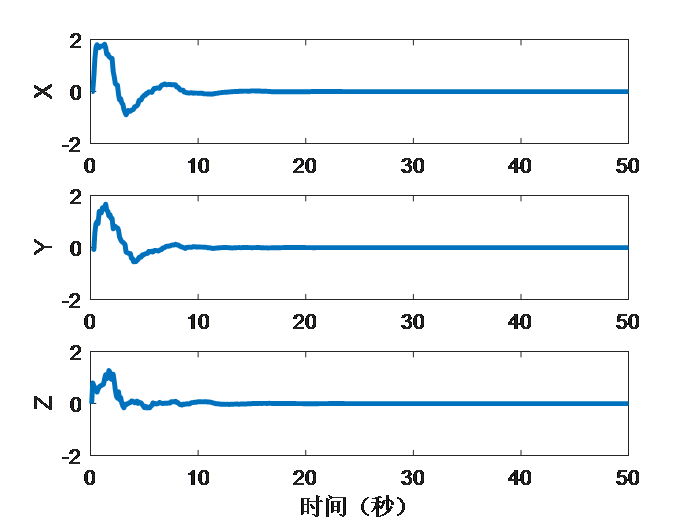
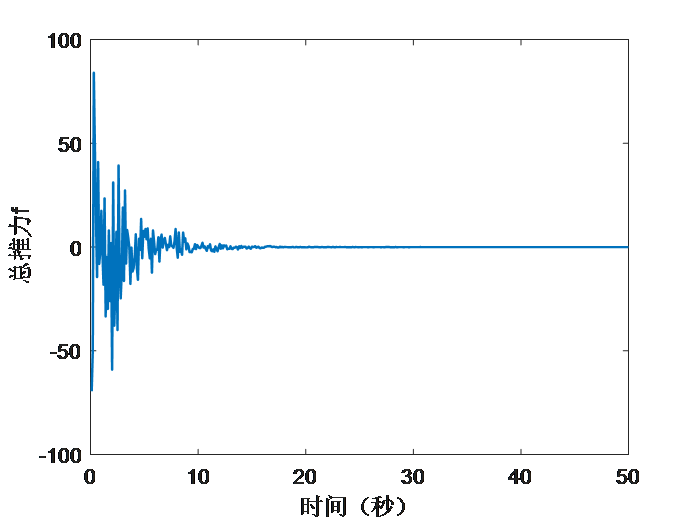
静态靶单点定位仿真实验的仿真结果如图3.4和图3.5所示。由图3.4可以看出,四旋翼无人机从原点起飞,最终以螺旋形的轨迹接近期望的终点(蓝色星星)。由图3.5(a)可以看出,x,y轴向的位置误差经过了超调,而z轴向则没有超调,在10秒左右时,三个轴向的误差大致为0,后续波动较小,此时四旋翼无人机接近指定位置,说明了单点定位的响应快速性;由图3.5(b)可以看出,在初始阶段,总推力的波动较大,当10秒后四旋翼无人机接近指定位置后,基本不变,接近四旋翼无人机的重力大小,此时四旋翼无人机进行空中定点悬停;图3.5(c)中,速度误差与位置误差相似,在10秒后达到稳态;由图3.5(d)中可以看出,在仿真过程中,力矩一直处于抖动状态,说明四旋翼无人机在不断地调整姿态。
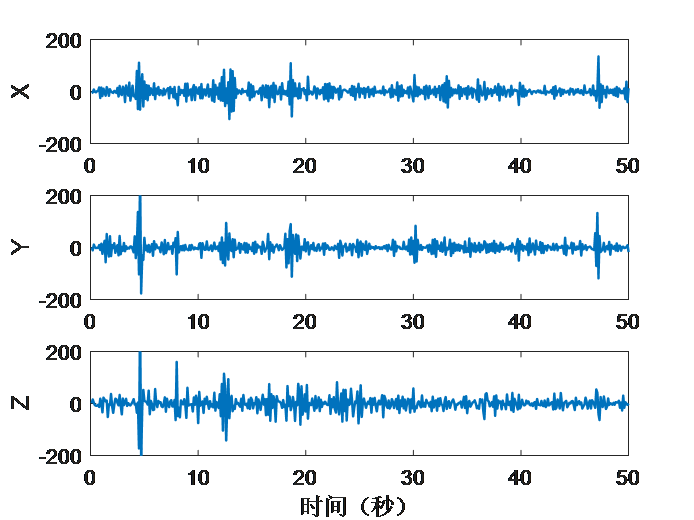
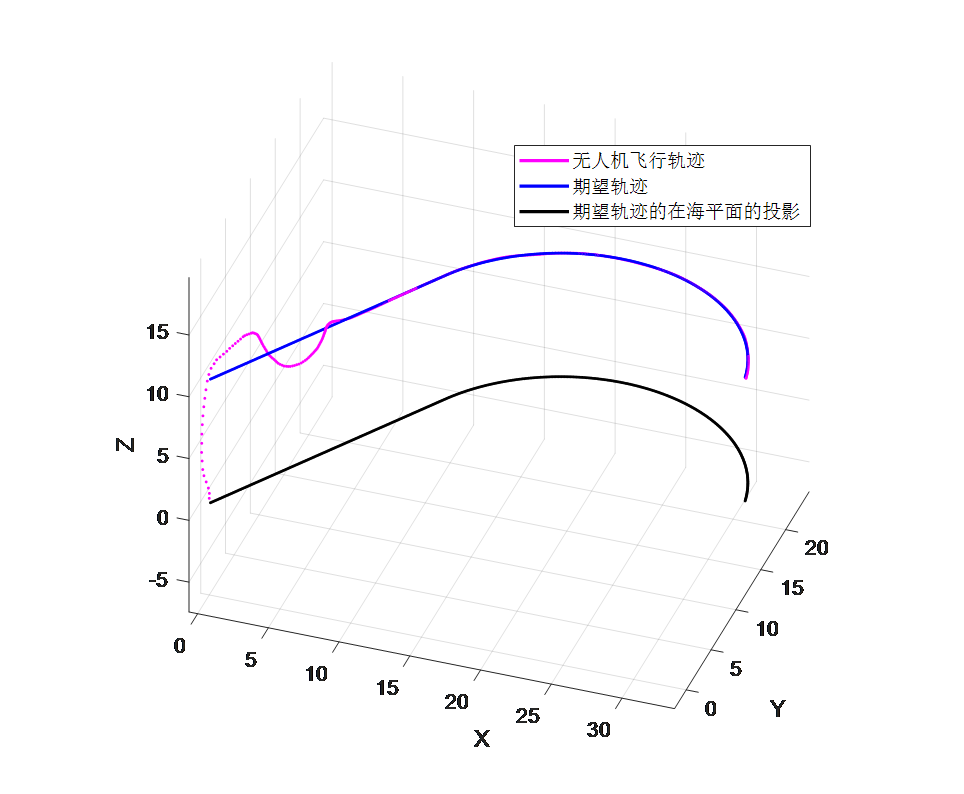
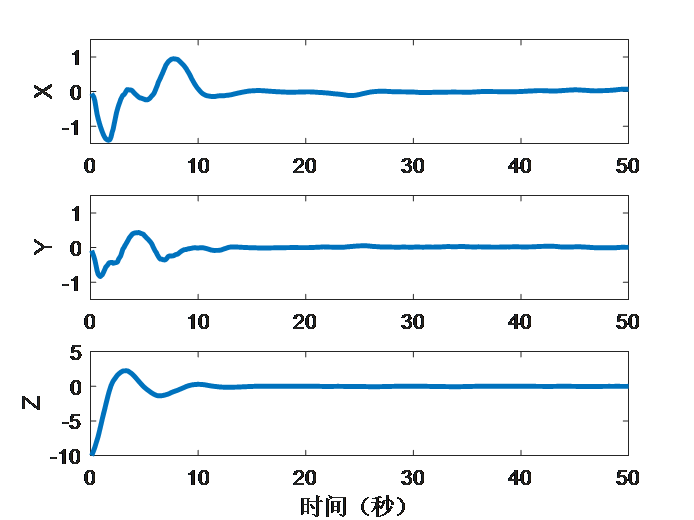
动态靶路径跟踪仿真实验的仿真结果如图3.6和图3.7所示。由图3.6可以看出,四旋翼无人机从原点起飞,在经历了两次超调之后,追踪上移动轨迹,其后四旋翼无人机的飞行轨迹(粉红线)与期望的轨迹(蓝色线)基本重合,跟踪误差较小,证明了该控制器优异的跟踪性能。由图3.7(a)可以看出,x,y,z轴向的位置误差均经历了超调,在15秒左右时,三个轴向的误差大致为0,后续波动较小,此时四旋翼无人机跟踪上指定路径轨迹,说明了路径跟踪的响应快速性;由图3.7(b)可以看出,在初始阶段,总推力的波动较大,当15秒后四旋翼无人机跟踪上指定路径轨迹后,由于给指定路径在z轴上无变化,所以基本不变,接近四旋翼无人机的重力大小,以保证四旋翼无人机飞行高度维持不变;图3.7(c)中,速度误差与位置误差相似,在15秒后基本达到稳态;由图3.7(d)中可以看出,在仿真过程中,力矩一直处于抖动状态,说明四旋翼无人机在不断地调整姿态。
通过上述的静态靶单点定位和动态靶路径跟踪仿真实验,验证了四旋翼无人机的动力学方程的可行性和路径跟踪算法的快速响应性及优异的跟踪性能。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: