一类椭圆辛映射的规范型毕业论文
2020-07-08 21:48:06
摘 要
本文讨论了辛映射这一作为哈密顿系统的离散形式,继承了哈密顿系统的一些性质。同时因为辛映射没有固定的规范型,因而在处理小分母问题时,会有很多困难。因此为了解决辛映射的小分母问题,我们针对椭圆构造了相应的非共振条件,并在此基础上进行迭代,来寻找在Russmann非退化条件下近似可积辛映射低维椭圆的规范型。
关键词:KAM定理;小分母问题;低维椭圆;规范型
Abstract
In this paper, we consider the symplectic mapping as a discrete form of Hamiltonian system and inherit some properties of Hamiltonian system. At the same time, because the symplectic map has no fixed norms, there are many difficulties in dealing with the problem of small denominator. Therefore, in order to understand the problem of the small denominator of the symplectic mapping, we construct the corresponding non resonance conditions for different cases and iterate on this basis to find the normal form of the approximate integrable symplectic mappings for the low dimensional ellipse under the Russmann non degenerate condition.
Keywords: KAM theorem; small denominator problem; low dimensional ellipse; normal form
目 录
摘 要 I
Abstract I
第一章 引言和研究背景 1
1.1 KAM理论 1
1.2 辛矩阵 2
1.3 辛同胚 2
1.4 生成函数 3
1.5 哈密顿系统 3
1.6 KAM迭代引理 3
1.7 小分母问题背景及由来 6
1.8 高维小分母问题的研究 8
第二章 问题的研究与解决 10
2.1 KAM迭代引理的证明 10
2.2低维椭圆的研究 11
2.3迭代的收敛 17
2.4具体椭圆规范型的求解示例 22
参考文献 24
致谢 27
第一章 引言和研究背景
1.1 KAM理论
1950至1960年,科尔莫哥洛夫(Kolmogorov)、阿诺德(Arnold),莫塞尔(Moser)(K.A.M)开发了一套研究近可积分哈密顿系统动态稳定性的理论——古典KAM理论。从那以后,哈密顿系统和映射的动力学高速发展。KAM理论处理的是近可积哈密顿系统的不变环面存在性和运动稳定性问题,近可积分哈密顿系统是由干扰项与可积哈密顿两个部分组成的, 近扭转映射是与近可积哈密顿系统相对应的映射。1962年,莫塞尔(Moser)建立了扭转定理,奠定了辛映射KAM理论的研究基础。。从那以后,哈密顿动力学系统和映射的动力学快速地发展。
在近代,在研究哈密顿系统的时候,KAM理论也逐步开始应用于其中,KAM理论的发展也愈发广泛。在不同非退化条件[1,2,6]下的研究产生了各种KAM定理,其中Russmann[22,23]提出的非退化条件是最弱的。在KAM理论中,KAM不变圆环的规律性是一个需要考虑的重要问题,因为小的除数总会造成光滑度的损失。Pöoschel[18]证明了持续不变的环面在频率参数中是C∞平滑的。之后Popov[20]在科尔莫哥洛夫(Kolmogorov)非简并度条件下,在其频率中得到了不变圆环量的Gevrey光滑性。然后Xu和You [29]将结果扩展到Russmann非简并条件的情况[30,31]。中的研究产生了低维不变圆环的结果。除了哈密尔顿系统外,从莫塞尔(Moser)的关于区域保存映射的著作[14,15]来看,已经证明映射的KAM定理[3-5,7-10,22,27]。
哈密顿函数具有形式
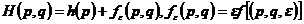
其中£非常小,作用变量p=(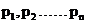 )
)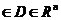 ,q=(
,q=(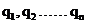 )
)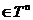 ,其中
,其中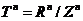 通常是n维环面。
通常是n维环面。
相应的运动方程是
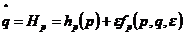 ,
,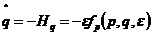
它的相空间是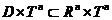 .这里假设自由度n不会低于2。
.这里假设自由度n不会低于2。
非退化条件的研究成为KAM理论的重要内容和创新。
1954年科尔莫哥洛夫(Kolmogorov)在非退化条件下给出了一个定理:
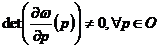
在1971,Bruno提出了一个较弱的方法:
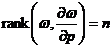
这就是所谓的Bruno非退化条件。在1990,Rüssmann在弱非退化条件下给出了解析哈密顿系统的KAM定理:
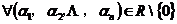
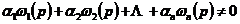
1.2 辛矩阵
定于一个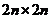 矩阵
矩阵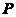 有
有
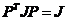 , (1.1)
, (1.1)
您可能感兴趣的文章
- 腐败与美国各州收入不平等之间的关系:来自专家小组的协整和误差修正模型的证据外文翻译资料
- 内蒙古1962 – 2016年时间序列气候变量的变化特征外文翻译资料
- 残差修正法在季节性ARIMA电力需求预测中的应用:以中国为例外文翻译资料
- 净工资与居民消费价格指数的关系分析外文翻译资料
- 我国鸡蛋价格波动的深入研究与预测外文翻译资料
- 信赖域与线搜索技术的结合外文翻译资料
- 求解奇异非线性方程组的多点LM方法外文翻译资料
- 具有双线性和非单调发病率的关于两个菌株的流行病模型的全局稳定性分析外文翻译资料
- 寻找可伸缩的区块链结构: 工作证明与BFT复制外文翻译资料
- 网络营销中潜在成功人士的结构方程建模外文翻译资料




