参数未知时带链规则控制图对生产质量过程控制毕业论文
2020-02-15 23:37:49
摘 要
本文主要对休哈特控制图和2-of-3带链规则控制图在参数已知和参数未知情况下的ARL(Average Run Length,平均运行长度)和SDRL(Standard Deviation Run Length,运行长度的标准差)分析建模,并用MATLAB软件对模型进行了编程求解。然后分析了每个控制图在过程参数已知和未知情况下的性能,并将两种控制图性能进行了比较分析。
研究结果表明:当过程参数已知和过程参数未知时,除非样本数m很大,否则属性(c.d.f,p.d.f,ARL,SDRL)是完全不同的。由于实际上和经济上都不可能获得大量的阶段一样本,所以在参数未知的情况下,不能使用参数已知情况下的常数K值。而无论是参数已知情况下还是参数未知情况下,在生产质量控制过程中,2-of-3带链规则控制图的性能要优于休哈特控制图的性能,其能更好地监测平均偏移,及时告警。
关键词:控制图;马尔科夫链;链规则;链长属性
Abstract
In this paper, the ARL and SDRL models of Shewhart control chart and 2-of-3 Run Rules control chart with known and unknown parameters are analyzed and solved with Matlab software. Then the performance of each control chart is analyzed when process parameters are known and unknown, and the performance of the two control charts is compared and analyzed.
The results show that the attributes (c.d.f, p.d.f, ARL, SDRL) are completely different when the process parameters are known and unknown, unless the sample number m is very large. Since it is practically and economically impossible to obtain a large number of stage samples, the constant K with known parameters can not be used when the parameters are unknown. In the process of production quality control, the performance of 2-of-3 Run Rules control chart is better than that of Shewhart control chart, which can monitor the average deviation better and warn in time, whether the parameters are known or not.
Key Words: control chart; Markov chain; Run Rules; run length
目录
第1章 绪论 1
1.1 背景 1
1.2 论文研究的意义 1
1.3 国内外研究现状 2
1.3.1 国内研究现状 2
1.3.2 国外研究现状 3
1.4 论文的研究内容 3
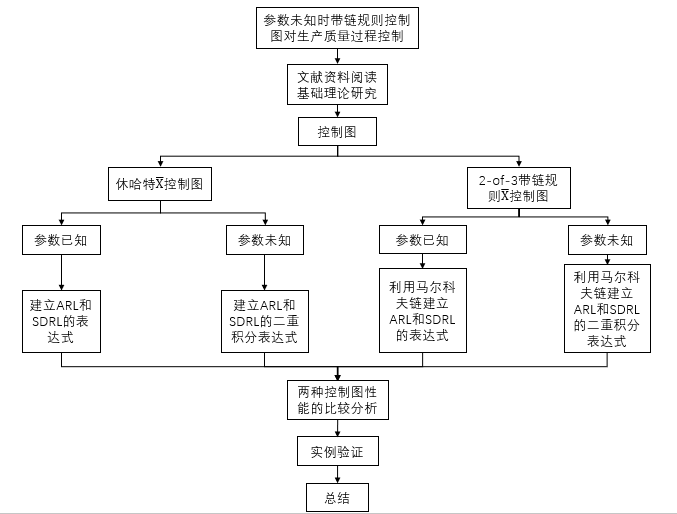
1.5 论文的研究方法及技术路线图 4
1.5.1 论文的研究方法 4
1.5.2 技术路线图 5
1.6 小结 5
第2章 休哈特控制图 6
2.1 具有已知参数的休哈特控制图的属性 7
2.2 具有未知参数的休哈特控制图的属性 10
2.3 小结 15
第3章 2-of-3带链规则控制图 17
3.1 具有已知参数的2-of-3带链规则控制图的链长属性 17
3.2 具有未知参数的2-of-3带链规则控制图的链长属性 20
3.3 小结 23
第4章 实例验证 25
4.1 休哈特控制图 25
4.1.1 参数已知 25
4.1.2 参数未知 25
4.2 2-of-3带链规则控制图 25
4.2.1 参数已知 25
4.2.2 参数未知 26
4.3 小结 27
第5章 总结 28
5.1 经济性分析 28
5.2 环保性分析 28
5.3 总结 28
5.4 展望 29
参考文献 30
附录A 32
附录B 33
附录C 35
附录D 37
附录E 39
致 谢 40
第1章 绪论
1.1 背景
目前,质量不仅是企业发展的重点,而且也是企业在变化迅速的市场中生存下来的决定性因素之一。在以前的生产过程中,一般采用的是加强检验的方法来保证产品的质量,但这种措施只是在发生异常后进行补救的一种措施,仍然会有不合格品的产生。因为质量是在生产过程中产生的而不是检验出来的,所以提高生产过程的质量,实现对生产过程的监控,及时告警以预防不合格品的发生,已经变成质量管理中一个特别重要的课题。
在工业迅速发展的今天,由于信息技术的日益成熟,其已充分应用到制造业中。目前的生产制造企业将统计过程控制(Statistical Process Control,SPC)作为质量管理的主要方法[1]。统计过程控制就是利用统计数据监控过程中的各个阶段并利用控制图对质量进行管理以控制和提高产品质量。其目的是通过对生产过程的实时监控,科学地识别产品质量的随机和异常波动并对异常状态进行预警以及时采取措施来消除异常和恢复生产过程的稳定性,从而提高产品质量和工作效率。
SPC的本质是利用样本信息来判定生产过程是否受控并采取相应措施来减少异常因素对生产过程的影响,从而降低质量成本和提高产品质量。当只有随机因素影响时生产过程处于受控状态;当生产过程受系统因素影响时则处于失控状态。SPC是利用过程波动的规律对生产过程质量进行分析和控制的。其利用图表等分析工具将产品的特征转化为数据,再利用计算方法对产品特征进行统计分析以变成对提高产品质量有帮助的信息,然后通过分析这些得到的信息来做出相应的决策以提高产品质量和降低生产成本。统计过程控制强调的是对整个过程的预防和控制,其最初用于生产管理,后来扩展到其他方面。
20世纪20年代,美国的休哈特(W.A.Shewhart)提出了统计过程控制理论和统计控制过程的重要工具即控制图以控制产品的生产过程。而控制图既可以显示出质量波动状态又能监测和指导过程,在生产质量过程控制中起到很大的作用。因此,了解各种控制图的性能,并将其应用到合适的生产过程中可以大大提高生产质量。如休哈特控制图就可以很快地发现生产过程中的大偏移。同时还可以对控制图进行优化使其具有很好的性能,比如将链规则应用到休哈特控制图中可以提高其对生产过程的小、中偏移的敏感性,可以更及时地发现生产过程中的失控状态,以采取措施减少损失,提高生产质量。故控制图对生产质量控制有很大的作用。
1.2 论文研究的意义
质量管理的主要任务之一是找出过程的波动的规律并且将正常的波动控制到最小以消除因为系统因素引起的异常波动。而质量控制可以将实际测得的质量特性值与相应标准进行比较并采取相应措施来改正差异或者消除异常情况,从而使过程保持受控状态。因此,一个好的质量控制标准是很重要的,并且好的质量管理可以为企业创造很多价值。
利用统计方法对过程中的各个阶段进行监控的目的是及时发现问题并及时采取措施以保证过程质量,即进行统计过程控制的过程中需要贯彻预防的原则。因此合适且高效的统计过程控制方法不仅可以为质量管理提供强有力的理论依据还可以发现生产过程中的薄弱环节,及时告警以对生产过程进行控制。
控制图是具有控制和分析功能的判断生产过程是否处于受控状态的一种方式。它不仅可以对过程进行评估以确定过程是否能够顺利进行而且还可以监控生产过程并及时预警以防止出现不合格品。使用控制图是为了通过产品质量特性值在图上的分布情况来判定生产过程是否受控,如果发现异常则要及时采取相应措施使生产过程回到受控状态。所以控制图是进行生产质量过程控制的非常有效的工具,对控制图的深入研究和优化对生产质量控制是非常有意义的。
标准休哈特控制图的样本容量和抽样区间是固定的,即每隔固定的时间段从过程中抽取固定容量的样本,如果样本均值超过了控制界限则判断过程失控。休哈特控制图不仅操作简单,还可以更快检测过程的大偏移。休哈特控制图对过程中、小偏移检测能力较弱,而链规则的使用可以增加休哈特控制图对过程偏移的敏感性。
为了提高休哈特控制图对小到中度变化的敏感性,进而提高企业的生产质量,降低质量成本,适当将链规则与休哈特控制图结合可以获得更好的监控效果。一般控制图的性能是通过平均链长(Average Run Length,ARL)来评价的。然而实际上,数据和过程参数很少为人所知,且参数通常是从可控历史数据集中估计出来的,在这种情况下控制图的性能与参数已知情况下不同[2]。因此,本设计将研究参数未知时带链规则控制图对生产质量过程的影响。
1.3 国内外研究现状
1.3.1 国内研究现状
国内对控制图的优化研究比较多,如郭宝才,孙立荣将一种链规则和可变样本容量的思想一起并入休哈特控制图让其对过程均值的小偏移更敏感并利用马尔科夫链方法计算了控制图稳态下的平均链长[3]。张宇波等改进了传统休哈特控制图的算法,在预测模型的基础上将以前和当前的观测值关联来获得更多信息,以便能较好地反映较小偏移的变化[4]。针对过程数据存在异常值的问题,胡雪龙等采用中位数统计量代替了均值统计量,提出了一种新的带链规则的控制图(Run Rules ,RR—)来监控过程均值偏移[5]。
而参数未知情况下,对于过程方差估计不准确的情况,胡雪龙等用t统计量代替了均值统计量,提出一种链长t控制图来监控过程均值偏移并使用马尔科夫链方法构建了该控制图的状态转移矩阵,推导出了平均运行链长指标[6]。
1.3.2 国外研究现状
国外对马尔科夫链以及带链规则控制图的研究较多,如Champ,Woodall推导出了带链规则控制图的链长分布特性[7]。Palm等使用了马尔科夫链计算出了链长的指标[8]。Koo通过画图表示出了带有几种链规则的控制图的控制界限,并得出2-of-3带链规则控制图对中等规模偏移的检测效果较好而3-of-4带链规则控制图则对小规模的偏移更敏感 [9]。Castagliola等针对过程受控且均值和方差成比例变化的情况提出了带链规则的变差系数控制图[10]。考虑到偏移大小的不确定性,Tran等研究了带链规则控制图的性能以监控两个正态变量的比值[11]。
当参数未知时,Castagliola等研究了控制图的性能并推导了参数未知情况下的控制图的链长指标 [12]。Castagliola等推导了参数未知情况下的EWMA控制图的链长指标,研究了参数未知情况下的EWMA控制图的性能 [13]。Hu等在过程参数未知情况下,采用Bootstrap方法调整了控制图的控制界限,极大改善了其受控状态下的性能[14]。Celano等将变样本容量、变抽样区间和链规则一起并入了休哈特控制图[15]。
1.4 论文的研究内容
本文将深入分析2-of-3带链规则控制图的原理和特点,分析其在参数已知和未知情况下的性能,并与休哈特控制图进行比较,建立优化模型,提出过程参数未知情况下抽样大小和控制图参数的计算方法。同时熟悉和掌握MATLAB的编程语言和方法,并学会使用MATLAB对参数进行建模求解。
(1)休哈特控制图在过程参数已知和未知情况下的性能:
定义m组抽样大小为n的样本,建立模型表达参数已知情况下失控状态的值,建立方程求出不同的n值对应的不同K值,进而计算ARL和SDRL来分析均值控制图的性能;
在上一步的基础上建立模型表达出参数未知情况下的失控概率,定义U,V分别服从正太分布和伽马分布。将化简为关于U,V的式子,和上一步相同,建立方程求出不同m,n值对应的不同的K值,进而计算ARL和SDRL的值。当m,n取不同的值,分析不同情况下的参数已知和参数未知时的控制图的性能并进行对比分析。
(2)2-of-3带链规则控制图在过程参数已知和未知情况下的性能:
定义m组抽样大小为n的样本,熟悉2-of-3链规则的各个状态,用马尔可夫链矩阵P来定义2-of-3链规则的各个状态。定义2-of-3链规则均值控制图的概率密度函数和累计分布函数,可得带链规则均值控制图的、、。进而可得ARL和SDRL;当参数未知时,和休哈特控制图的方法类似,建立模型表达出、、。经过公式变换得到处于控制状态下的最终、、。由随机变量U、V的概率密度函数及以上可得参数未知时的概率密度函数、累计分布函数、ARL、SDRL。分析当样本大小n一定时,不同数值组合的平均偏量和样本组数m下的ARL1和SDRL1,进而对参数已知和未知情况下的性能进行比较分析。
(3) 用生产过程实例验证参数未知时带链规则控制图的性能:
找生产实例的数据,分别用休哈特控制图和2-of-3带链规则控制图在参数已知和参数未知情况下来进行计算和比较分析,以证明休哈特控制图检测过程中、小偏移的能力较弱,链规则的使用可以增加休哈特控制图对过程偏移的敏感性。
1.5 论文的研究方法及技术路线图
1.5.1 论文的研究方法
(1)查阅文献,学习马尔科夫链,具体了解休哈特控制图和2-of-3带链规则控制图的特性和属性计算方法以及这两种控制图在生产质量过程控制中的优缺点和适用情况。
(2)用马尔科夫链建立对2-of-3带链规则控制图的属性的计算方法。
(3)用MATLAB完成对这两种控制图的属性值的编程计算和结果汇总。
(4)用实例比较分析两种控制图的性能和对生产质量过程控制的影响。
1.5.2 技术路线图
1.6 小结
本章对论文的研究背景和意义进行了叙述,介绍了国内外关于课题的研究现状,对论文的研究内容和方法进行了简单介绍并画出了具体的技术路线图。
第2章 休哈特控制图
控制图是用于测定、记录选定的过程质量特性以便进行控制管理的用统计方法设计的图。如图2.1上有上控制界限(Upper Control Limit,UCL)、中心线(Central Line,CL)和下控制界限(Lower Control Limit ,LCL),样本点是按时间次序抽取并进行描点。控制图基于3准则,其功能在于通过图上的点子分布来及时告警过程中出现的问题。
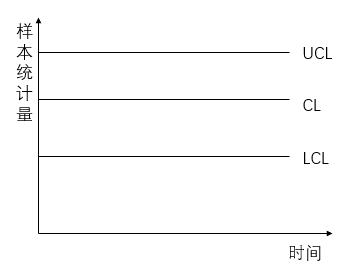 图2.1控制图
图2.1控制图
控制图的应用步骤:
(1)选定质量特性及控制图,对生产过程进行分析并确定合理的分组原则。
(2)收集预备数据画出分析用控制图,分析过程是否处于受控状态。
(3)和质量标准进行比较,画出控制用控制图来对生产过程进行监控。
 (4)修正中心线和控制界限。
(4)修正中心线和控制界限。
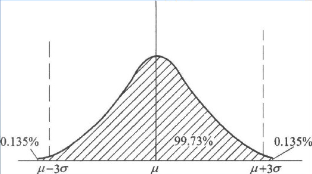
图2.2正态分布密度函数曲线
休哈特控制图的3原理:在图2.2正态分布密度函数曲线中可以看到,正态分布X~N()由两个参数,即总体均值和总体标准差来决定的。如果质量特性值X服从X~N(),当生产过程中仅有偶然性原因存在时可得测得的产品质量特性值X有99.27%的概率落在的范围内;而落在之外的概率为0.27%;超过一侧,即落在大于或小于的概率为0.135%。也可以说如果抽取少量产品,测得的产品的质量特性值都应该落在范围内,如果有特性值落在的界限外就可以认为过程出现系统性原因时X的分布发生了偏离。
控制图是一种用统计方法设计的被用于测量、记录、评价和监测过程是否处于控制状态的图表。其显示质量特性值随时间的波动曲线,并对质量波动是偶然原因还是系统原因造成的进行了分析和判断,从而给出预警以便及时对这种情况做出准确判断并采取有效的措施,消除了由于系统原因产生的影响,使生产过程得到稳定的控制。控制图是通过判别和区分正常质量波动和异常质量波动来调查、分析过程是否处于统计控制状态,以及保持过程处于通知控制状态的有效工具。其在生产过程中既可以显示出质量波动情况又可以调控过程,可以起到事先预防作用。
常规休哈特控制图分四种计量型控制图和四种计数型控制图。其中最常用、最重要的是适用于具有一定批量的连续生产过程的—R控制图。它可以同时控制质量特性值的集中趋势,即平均值的变化和极差的变化。它适用范围广,灵敏度高,可以提供较多的质量情报。
在生产过程中产品的质量受随机和系统这两种因素的影响。随机因素是由许多微小的偶然因素累加造成的,而系统因素是由可辨识的和明显的原因造成的,这两种因素都可以通过采取适当措施来发现和消除。控制状态是指当生产过程只受随机因素的影响,从而使产品质量特征的平均值和方差基本稳定的状态。在这种情况下,产品的质量特征的分布可以用统计方法根据较长时期在稳定状态下获得的观测数据估计。当分布确定后就可以确定质量特征的数学模型。为了检验后续的生产过程是否受控则需要检验上述质量特征是否符合这个数学模型。为此,每隔一定的时间就在生产线上取大小一定的样本并计算其质量特征,如果其数值符合这个数学模型,则认为生产过程处于控制状态,否则认为生产过程失控。这时需要考虑采取各种措施,包括停产检查,以查明并消除原因,从而恢复正常生产,不让失控状态继续下去。
2.1 具有已知参数的休哈特控制图的属性
阶段一是收集组数、大小一定的样本数据并以此样本平均值及方差作为参数未知情况下的均值和方差来使用。




