摘 要

纳什均衡问题是经济学中的基本问题，也是一个非常特殊的优化问题。本文考虑了信赖域方法在纳什均衡中的应用。本文提出了一种Jacobi型信赖域方法。该方法包括每个博弈玩家的不同信赖域，每个玩家控制的策略变量的试探步长根据各自的效用函数被计算，并且选择接受或者拒绝。然后，定义了一个基于所有个体效用函数的整体评价函数，用于更新信赖域。并提出了一种新的更新信赖域边界的非标准技术。并从理论层面证明此方法的全局收敛性并建立局部收敛的结果。通过数值模拟，对三种松弛算法和本文提出的信赖域算法进行比较，从算法的迭代次数和迭代时间方面详细分析了四个算法的效率。所得结果对于纳什均衡解的算法改进与创新具有重要的指导意义。

论文主要研究：求解标准纳什均衡问题的Jacobi型信赖域方法。

研究结果表明：此算法的高效性和对纳什均衡问题的适用性。

本文的特色：将Jacobi思想和信任域相结合来解决纳什均衡问题，提出了一种新的更新信赖域边界的非标准技术。并通过数值模拟进行算法比较。

关键词：纳什均衡；信赖域算法；收敛性分析；数值模拟

Abstract

The Nash equilibrium problem is a basic problem in economics and a very special optimization problem. This paper considers the application of the trust region method in Nash equilibrium. This paper proposes a Jacobi-type trust region method. The method includes different trust fields for each player, and the heuristic step size of each player-controlled strategy variable is calculated according to the respective utility function and is selected to accept or reject. Then, an overall evaluation function based on all individual utility functions is defined for updating the trust region. A new non-standard technology for updating the trust domain boundary is proposed. The global convergence of this method is proved from the theoretical level and the result of local convergence is established. Through numerical simulation, the three relaxation algorithms are compared with the trust region algorithm proposed in this paper. The efficiency of the four algorithms is analyzed in detail from the iteration number and iteration time of the algorithm. The obtained results have important guiding significance for the algorithm improvement and innovation of Nash equilibrium solution.

The main research of the thesis is the Jacobi-type trust region method for solving the standard Nash equilibrium problem.The results show that the algorithm is efficient and applicable to the Nash equilibrium problem.The characteristics of this paper: Combining Jacobi thought and trust domain to solve the Nash equilibrium problem, a new non-standard technology for updating the trust domain boundary is proposed. The algorithm is compared by numerical simulation.

Key Words：Nash equilibrium problem；trust region method；Convergence analysis；Numerical Simulation

目录

第一章 绪论 1

1.1 非合作合作博弈理论的发展 1

1.2 纳什均衡问题（NEP）模型介绍 3

1.3 纳什均衡问题的常见算法 4

1.4 相关研究与本文内容 6

第二章 信赖域方法 7

2.1 信赖域方法概述 7

2.2 求解纳什均衡问题的Jacobi类型的信赖域算法 9

2.3 算法流程 12

第三章 信赖域算法收敛性分析 14

3.1 收敛性分析 14

3.2 算法讨论 22

第四章 数值模拟 24

4.1 相同效用函数的二人博弈 24

4.2 不同效用函数的示例 26

第五章 工作总结与展望 29

参考文献 31

致 谢 32

附录 33

绪论

1.1 非合作合作博弈理论的发展

纳什均衡，即非合作博弈均衡，因著名数学家、经济学家约翰.纳什而得名。在纳什均衡理论中，假设存在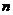个博弈玩家，每个博弈者根据其他玩家的策略方案来选择自己的最优策略，目的是让自己的利益最大化，所有玩家的策略选择构成一个策略组合。若在某个策略组合下任何一个玩家都不能只通过改变自身行为来提高个人利益，则把该策略组合称之为纳什均衡点。然而纳什均衡点不一定是全局最优的状态，引入上文经典的“囚徒困境”的示例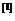：现有两名犯罪嫌疑人（用甲和乙分别代指）被捕后，进行隔离审讯，但由于证据不足，警察计划使用特殊的鼓励坦白的审讯策略—如果甲和乙都选择坦白则各判八年；如果一人坦白而另一人抵赖，则坦白者被释放，抵赖者将被判10年；如果都选择抵赖，由于证据不足只能各判一年。那么二人的所有可能选择的策略组合可以构建一个支付矩阵如下所示：

由上可见，如果二人均选择坦白，则任何一个人都没有动力单方面改变选择，因为不会获得更少的刑期。该策略组合即是一个纳什均衡点，但是我们可以发现如果二人均选择抵赖，他们将只会被各自判刑一年，达到整体利益最大化。这个经典的例子提醒我们，纳什均衡问题并不等同于整体最优化问题，而是寻找经过博弈之后各方达到的一种平衡状态：在该状态下的策略组合中，每个玩家都无法只通过单方面改变策略来获得更大的自身利益。

奥斯卡获奖电影《美丽心灵》讲述一位来自普林斯顿大学的杰出数学家，在与自身的精神疾病作斗争的同时，不断在博弈论和偏微分方程等多个领域做出卓越贡献，并最终获得诺贝尔经济学奖的故事。该片主角的原型即是约翰.纳什，由于在博弈论上令人惊叹的开创性成就，他与约翰.海萨尼和莱茵哈德.泽尔腾一起获得了1994年诺贝尔经济学奖。通过电影戏剧性的演绎，更多人开始走近并了解纳什均衡和博弈论。

早在纳什和博弈论的提出者冯.诺依曼之前，博弈论的思想已经开始在学术界萌芽。数学家波雷尔和梅洛，经济学家古诺、斯坦伯格、埃奇沃思等，都曾探索过博弈论的理论体系。博弈论起源于探究人们玩扑克牌、国际象棋等室内智力游戏时的相关行为决策。从体育竞赛到战争决策的所有关于策略的情景理论上都与博弈论有关，该理论创造性地提供了一个可以计算并比较各种可能决策所产生效益并由此做出决策的数学方法，为人们在各种相互竞争的情况下做出最优决策建立了一套具体可行的数学公式。

具体而言，1928年冯.诺依曼创立了二人零和博弈理论，但冯.诺依曼逐渐意识到：博弈论必须基于他的最大最小定理（该定理说明每个二人零和博弈均有一个解），。直到摩根斯滕与冯.诺依曼二人合著《博弈论与经济行为》一书，该书出版于1944年，并随即在学术界引起了强烈的反响，人们觉得通过博弈理论把经济学塑造成像自然科学一样可预测的学科满怀憧憬。《博弈论与经济行为》中的非合作博弈部分主要处理一类特殊的博弈—二人零和博弈。对于此类博弈。其结果是双方的支付之和均为0。冯.诺依曼和摩根斯滕认为这类博弈的合理解一般要求双方使用混合策略，即为了使对方无法知晓自己究竟采用那种策略，每个玩家会随机地选择自己的纯策略。至于各种纯策略将以怎样的概率来进行选择，冯.诺依曼和摩根斯滕在《博弈论与经济行为》一书的非合作部分指出：不管对方采用何种策略，他应该选择混合策略以保证期望支付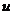不少于他的保障支付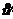的水平。他的保障支付水平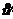是指能够得到保证的最大支付。一个玩家在计算其保障支付水平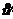时，率先计算运用每一个混合策略将得到的最小支付。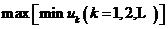所有这些最小支付的最大值即为保障支付水平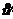。冯.诺依曼和摩根斯滕用于解释二人零和博弈的方法因此被称为“最大最小准则”，由于冯.诺依曼著名的最大最小定理断言博弈双方的保障支付水平之和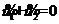，所以在二人零和博弈中运用最大最小准则是恰当的。与此同时冯.诺依曼提出二人零和博弈的均衡结果，是每一方应该恰好得到他的保障支付水平。

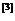但是，在经济学中人们并不太关心二人零和博弈，因为适用于这种理论的现实情景较少且不难分析，经济学家们着眼于如何把最大最小准则进一步推广到更为广泛的非零博弈之中。如果玩家I判断玩家II是理性经济人，并且知道理性人会使用最大最小准则，那么他自己会避免使用最大最小准则，而是采用作为相对于对方最大最小策略的最优反应的策略以此实现自身利益最大化。除非类似于在二人零和博弈，这个最优反应恰好是最大最小策略，否则当玩家II知道理性的玩家I知道玩家II是理性的，我们就会得到一种矛盾的结果。

纳什领先他人的贡献在于提出对冯.诺依曼最大最小定理推广的基础是这类最优反应的分析。一个策略组合要成为二人博弈的均衡解的基本条件是：其中每个策略必须是其他策略的最优反应。这样的策略组合，我们称之为纳什均衡，它是非合作博弈理论毫无争议的基础。纳什认为：如果一个非合作博弈有一个解，那么该解必是博弈的纳什均衡。

上世纪50年代，纳什开创性地完整阐述了“纳什均衡”的思想。与此同时，他的导师Tucker给出了著名的“囚徒困境”的问题。他们二人的研究工作为现代非合作博弈论的发展奠定了坚实的基础，随后越来越多的学者开始研究非合作博弈论。上世纪60至80年代是博弈论理论体系的快速发展阶段。1965年，Reinhard Selten论述了完美纳什均衡概念（subgame perfect Nash Equilibrium）。1967~1968年，John C Harsanyi阐述了贝叶斯纳什均衡概念（Beyesian Nash Equilibrium）。1982年，Wilson和Kreps共同创立了关于动态不完全信息博弈的相关理论。另外，Kreps，Milgrom，Roberts和Wilson于1982年一起建立“KMRW声誉模型”。

而在应用层面，博弈论已经被应用于许多领域之中。经济学家利用博弈论分析人们在商业行为中如何做出决策；生命科学家用它来探究物种进化的本质；历史学家使用它来研究几千年前的原始文化，从而说明人性的同一和差异；神经科学的学者们通过研究博弈者的脑神经，人们的情绪波动如何影响他们的决策。综上所述，科学家们在研究许多与人类行为相关问题时纳什的数学理论与在其基础上建立起来的现代博弈论往往能扮演重要角色。

1.2 纳什均衡问题（NEP）模型介绍

冯.诺依曼和摩根斯滕给出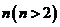人在串谋基础上进行的博弈的解的定义，但是该定义在预测玩家行为或者描述博弈值时的作用很弱。适用于博弈（或者经济情形）的适合的定义应该要求玩家可以自由提供或者接受作为对合作回报的转移支付（博弈规则之外）。智力游戏的传统理论道德告诉我们，非合作解概念（不考虑转移支付及博弈前的协商）更接近我们的现实目的，因此纳什均衡理论提出以下n人博弈模型。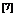

假设现有N个博弈玩家，玩家v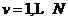（ ）通过控制策略变量 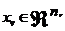来最小化其自身的效用函数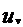（对应自身利益最大化）。令 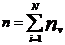为所有策略变量的总和，而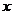可定义为一个策略组合

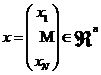
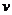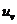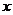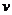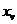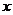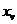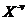第个玩家的效用函数 取决于整体策略组合。由于第个玩家可以控制自身的策略集，我们可以自然地将整体策略组合分成两个子部分：和，其中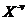是整体策略组合除去策略集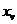后剩下的所有策略集。那么第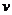个玩家的效用函数 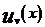可以表示为：

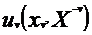
对于第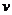个玩家而言，其目标是控制自身的策略集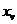使得效用函数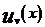最小化，记为：

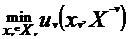
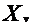其中 是玩家所有可能的策略集。通常 是一个紧凸集，并且被给定为

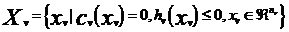
其中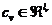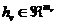，是定义于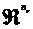的连续向量函数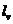（和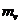是正整数）。此时一个策略组合点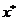是一个纳什均衡点，若该点满足