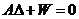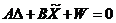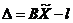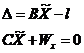水准网平差程序设计与实现毕业论文
2020-04-15 20:29:14
摘 要
近些年随着工程项目的不断增多,现代工程测量要求的精度不断提高,使得测量数据的处理非常关键,因此数据必须要经过精密平差,从而保证精度,才能为后续的工程项目开展打下厚实的根基。本文首先对编程语言和平差方法进行了分析,然后对所选取的平差模型原理与方法进行了介绍,并论述了水准网平差程序设计流程。基于C 语言,在Visual C 6.0环境下编写了一个平差程序,实现水准测量观测数据手动输入和平差结果以文本形式输出,最后依据实例对程序的可行性与正确性进行了验证。
关键词:水准网平差 平差模型 程序设计 C
.
Design and implementation of the Leveling network Adjustment program
Abstract
In recent years, with the continuous increase of engineering projects, the accuracy of modern engineering measurement requirements has been continuously improved, making the processing of measurement data particularly important.Therefore, the data must be strictly adjusted to ensure the accuracy, so as to lay a solid foundation for subsequent engineering projects.This paper first analyzes the programming language and the method of adjustment, then introduces the principle and method of the selected adjustment model, and discusses the programming flow of leveling net adjustment. Based on C language, a adjustment program was programmed in Visual C 6.0 environment, which realizes manual input and output of leveling observation data and difference results in text form. Finally, we verified the feasibility and correctness of the program by an example.
Keywords:Leveling network adjustment;Adjustment model;programming;C
目录
摘 要 I
Abstract II
第一章 绪论 1
1.1 研究背景 1
1.2 研究方法 1
1.2.1 编程语言分析 1
1.2.2 平差模型分析 2
第二章 间接平差模型 5
2.1 间接平差的原理 5
2.2 水准测量的权 7
2.3 精度评定 9
第三章 平差程序设计 11
3.1 原始数据文件格式设计 11
3.2 观测数据存储 12
3.3 近似高程的计算 13
3.4 法方程计算 16
3.5 残差计算 17
3.6 精度估计 18
3.7 平差结果输出 18
第四章 实例验证 20
第五章 结语 24
参考文献 25
致谢 27
绪论
1.1 研究背景
随着科学技术水平和社会需求的提高,国家全力推展各种基础性设施建设,随之应运而生了许多的工程项目,而且现代工程的需求持续上升,各种工程当中所要求的精度越来越高,为了满足基础设施工程建设的需求,工程项目当中数据的处理就显现得非常重要,所以在计算当中必须要对测量数据进行严谨的平差,保证精度要求[1],但是测绘工作的内业数据处理因为其数据量庞大、计算繁琐复杂、耗时比较长并且容易出现错误,所以一直以来给测量人员带来很多不便。随着计算机技术的不断发展和测绘行业对计算机辅助作业的需求越来越大,在取得了达到要求的观测数据之后就要对高精度水准测量中布设的水准网进行数据处理,在平差时人工手算耗时耗力、效率低下、精度不高且容易出错,所以各种各样的现代平差软件就随之出现。与传统的测量人员手工平差计算相比,平差程序对数据进行处理的优点主要表现在计算速度快、结果精度高、数据处理可实现自动化,能够将内业处理人员从繁琐复杂的平差计算工作中解放出来,所以在工程测量当中能够被广泛使用。本文以观测高差值作为起算数据,已知点的高程为基准,采取间接平差法,基于C 程序语言编写一个平差程序能够实现对外业测量数据进行处理、精度评定和结果输出。
1.2 研究方法
1.2.1 编程语言分析
测绘学是一门有着悠久历史的古老学科,近年来随着科学技术的不断进步,测量技术正向着自动化的方向不断发展,使得测绘行业对计算机辅助作业的需求越来越大,对于平差程序来说,选择一个合适的语言编写是非常重要的。
C语言作为一个传统的面向过程的通用程序设计语言,具有功能全面、表达能力强、应用广泛、可移植性好等特点,适合编写一些底层驱动程序和内嵌应用程序,但对于处理复杂的问题,需要高度的抽象和建模时,C语言其实不合适。因此在C语言的基础上,通过面向对象的这一思维方式扩展了C语言,逐渐完善形成了C 语言。但C语言和C 有着很大的不同,在面对问题的处理思维方式上C语言是面向过程的语言,而C 却没有面向过程这一特点,它是一门通过面向对象来处理问题的语言。对于平差程序来说,其程序设计与其它程序设计思路相同,应该有着程序结构化设计流程,具有很好的延展性可以完善程序功能需求和适应性强,便于移植的要求。
对于面向过程的C语言来说,其程序本质就是通过一个或几个函数的调用了来实现一个功能,程序的结构为程序=算法 数据结构,算法和数据节后两者相互独立,这种特性不适合平差程序。C 语言是面向对象的语言,其基本特征中的封装、继承特点非常适合编写平差程序,封装能够将程序的具体实现环节给封闭掩盖起来,使得程序代码一体化;继承则可以扩充已存在的类,它们的目的都是可以多次调用代码,通过将程序算法和相关数据封装在一个对象中,然后程序设计出所需要的各种类和对象,在向有关对象发送操作指令,就可以完成程序所需要执行的任务。概括来说就是 对象=算法 数据结构;程序=对象 指令。由于C 的封装特性非常适合平差程序的编写,并且C 语言本身具有具有良好的扩展性和移植性,所以设计思路是将平差程序设计成一个C 类,考虑到代码的重复利用和功能划分,将C 类的成员函数设计成两类,一类是可以被重复利用、功能单一的函数,一类是能够完成计算功能的函数,程序通过调用两类函数来实现平差计算[8]。
1.2.2 平差模型分析
水准网是为了确定地面点的高程而布设的控制网,高程控制网是大地控制网的一部分,高程控制网用水准测量方法建立,一般采用从整体到局部,逐级建立控制的原则,按次序与精度可以分为一、二、三、四等水准测量[3]。在进行内业处理时,人工希望能够尽量减少计算工作量从而会选择不同的平差方法来应对不同的水准网,但计算机程序的快速高效性可以不考虑计算量这个问题,而把主要的焦点放在方法的规律性上面。
平差的方法有很多种,比如说条件平差、附有参数的条件平差、间接平差、附有限制条件的间接平差、序贯平差、秩亏自由网平差等[1]。不同的水准网网形和条件有着不同的平差方法,一个平差问题,无论采用条件平差还是间接平差,其最小二乘解是唯一的和一致的,即它与采用的具体平差方法无关[4]。虽然说不同的平差方法所得到的最终结果应当是相同的,但对于程序编写来说,形式统一且规律性强的方法则更加适合。下面对不同的平差方法进行了对比结果见下表1-1:
表1-1 4种平差模型比较
因素 平差模型 | 条件平差 | 附有参数的条件平差 | 间接平差 | 附有限制条件的间接平差 |
观测数 | n | n | n | n |
必要观测数 | t | t | t | t |
多余观测数 | r=n-t | r=n-t | r=n-t | r=n-t |
所设参数 | 0 | 0lt;ult;t且独立 | u=t且独立 | ugt;t且包含t个独立 |
方程数 | r | c=r u | r u=n | r u=n s |
待求量数 | n | n u | n u | n u |
方程形式 |
|
|
|
|
条件平差是依据多余观测数r列出r个条件方程,在列立方程时要遵循足数,即条件方程个数=多余观测数;独立,即条件方程之间必须相互独立;最简,即在选择方程时必须优先选则形式较为简单、容易列出的条件方程的原则。如果说一个几何模型可以列出多个条件方程,但是在选择方程时,必须要从中选择形式最为简单的并且r个彼此线型无关的条件方程,对于复杂的平差问题就不好确定到底选用哪一个方程,假如一旦选择错了条件方程,那么就会给后面的平差计算带来诸多的麻烦。另外,条件平差在计算时最终所获得的结果是观测值的改正数,并非是观测值的平差值,平差值还需要由观测值加改正数求得,这进一步加大计算工作量。因此这些缺点使得条件平差法不太适合作为平差程序的数学模型。
处理平差问题时,我们在条件平差的条件方程基础上又选择了若干个含参变量,其数量为u来参加平差计算,且变量个数u不超过t个,故一共列立了r u个条件方程,从而建立了有含参变量参加计算的条件方程来作为平差模型,称这样的平差方法叫附有参数的条件平差。在平差程序设计方面,这两个平差方法有着相似的优劣点,它们条件方程的选择多样,误差方程形式规律性不够强,如果一旦选择错了条件方程会给后续的计算增添麻烦,故不宜作为设计的平差模型。