M50NiL钢高温条件下奥氏体晶粒变化研究毕业论文
2020-03-12 10:33:24
摘 要
Abstract IV
1 绪论 1
1.1 引言 1
1.2 关于M50NiL钢的研究 2
1.2.1 M50NiL钢简介 2
1.2.2 国内外研究现状 2
2 奥氏体晶粒生长理论及模型 3
2.1 晶粒长大原理 3
2.2 奥氏体晶粒生长动力学模型 5
2.2.1 Beck模型简介 5
2.2.2 Hillert模型简介 6
2.2.3 Sellars模型简介 7
3 实验材料及实验方案 10
3.1 实验材料 10
3.2 实验方案 10
3.3 M50NiL钢显微组织观察 10
4 M50NiL钢奥氏体晶粒生长行为研究 11
4.1 引言 11
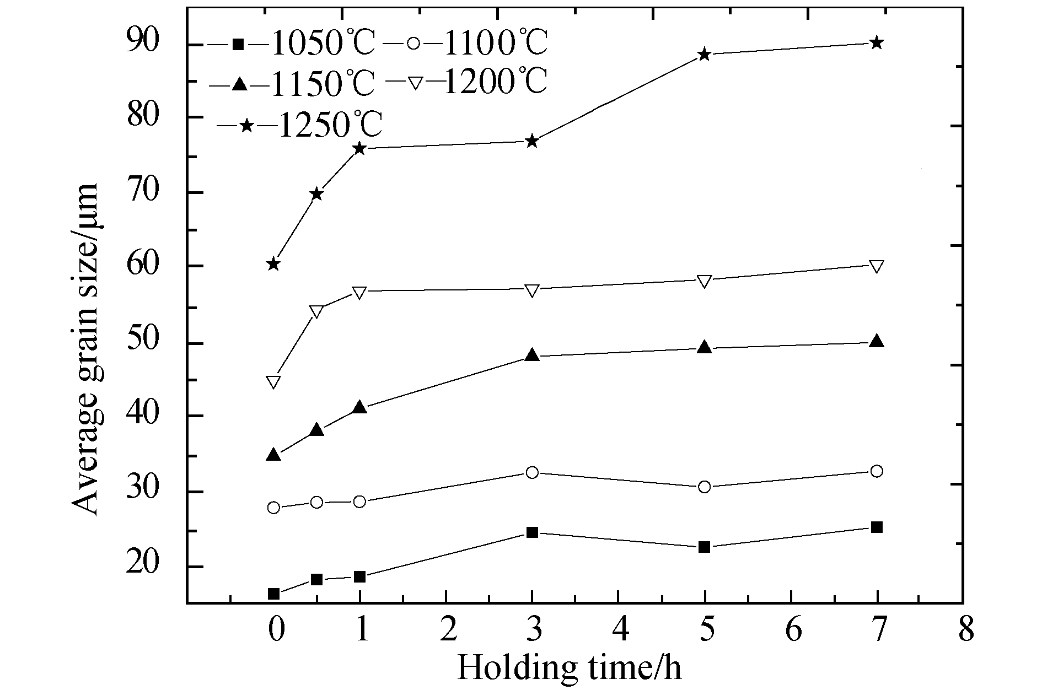
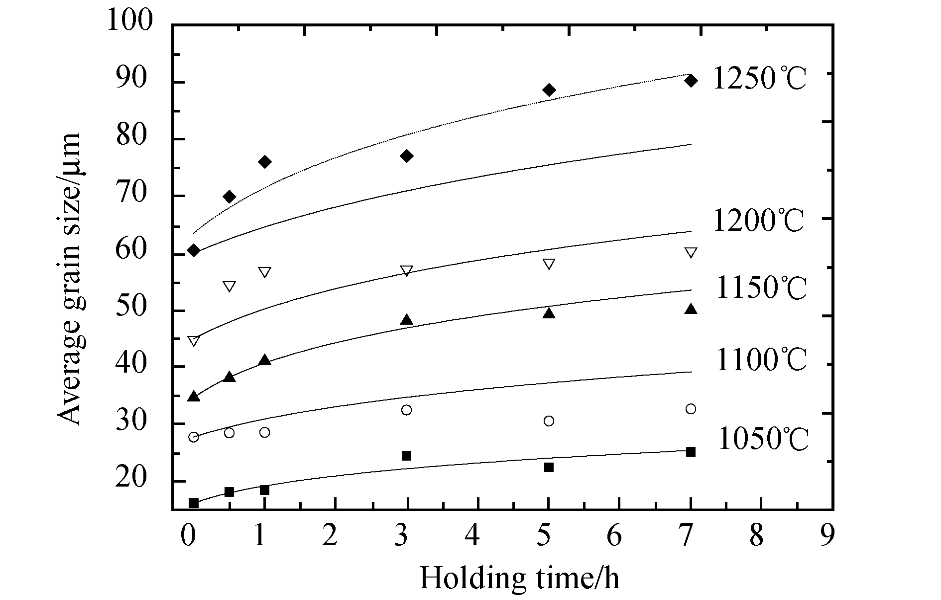
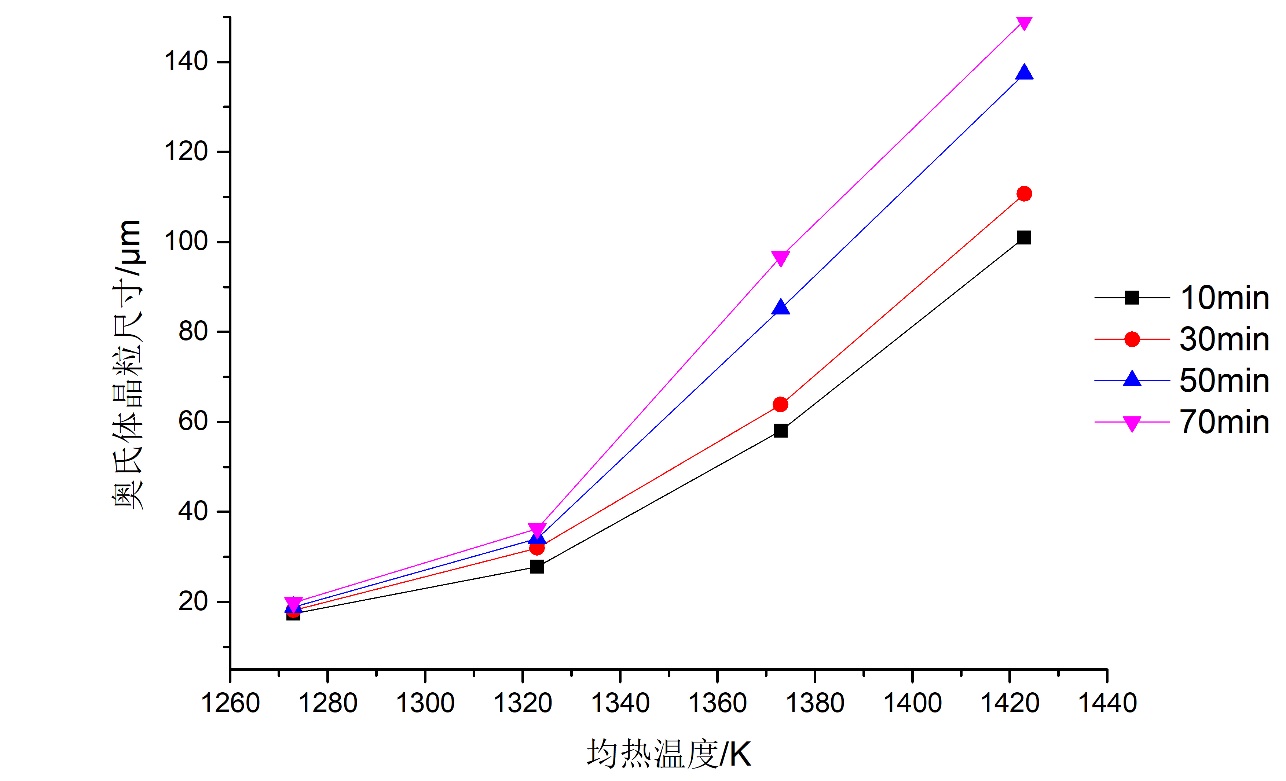
4.2 加热保温后的奥氏体晶粒尺寸 11
4.3 回火温度与M50NiL钢奥氏体晶粒直径的关系 12
4.4 恒温时间与M50NiL钢奥氏体晶粒直径的关系 14
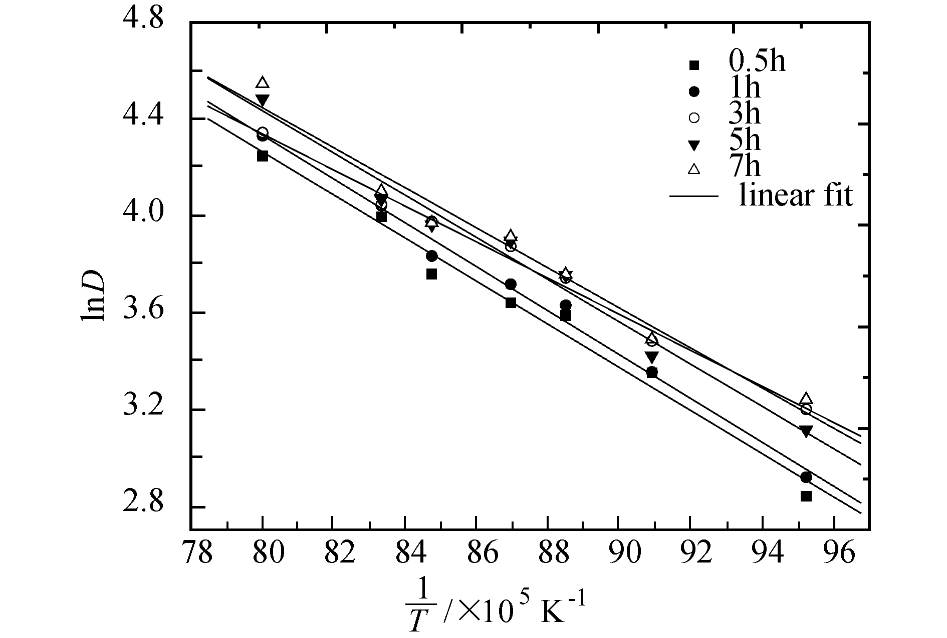
4.5 M50NiL钢奥氏体晶粒生长模型 15
4.5.1 Beck模型及其应用 15
4.5.2 Hillert模型及其应用 18
4.5.3 Sellars模型及其应用 20
4.5.4 分析与讨论 23
5 论文总结 24
参考文献 25
致 谢 27
摘 要
M50NiL钢是在M50轴承钢的基础上研制的第二代高温高合金低碳轴承钢,同时也是一种易于渗碳、渗氮的合金钢,经过复合化学热处理工艺后可以得到“外硬内韧”的特性,另外由于在复合化学热处理后表层产生了残余应力,大幅提高了该钢种作为轴承套圈的寿命,所以在航空航天上应用十分广泛。作为航空航天部件,对其晶粒细化程度有着严格的要求。然而,M50NiL钢的热锻工艺区间较窄,锻件的晶粒度不易控制,给实际生产带来了许多困难。本文通过加热保温实验研究了M50NiL钢的奥氏体晶粒生长模型,并使用不同的模型对数据进行回归运算。
本文首先根据与Beck、Hillert和Sellars模型相关的文献,分别说明了各个模型的原理,使用方法以及精确度分析过程。随后结合原理分析了影响M50NiL钢奥氏体晶粒生长的影响因素及其原理,据此制定了详细的实验方案。利用金相实验的方法得到在不同工艺条件下的M50NiL钢奥氏体晶粒的平均晶粒尺寸,使用三种模型研究其在回火温度为1000℃~1150℃、恒温时间为10分钟~70分钟下的奥氏体长大动力学模型,并研究了各个模型的优势与缺点。最后决定使用Sellars模型来描述M50NiL钢奥氏体晶粒的长大行为,得到M50NiL钢奥氏体晶粒生长动力学模型为:。
关键词:晶粒生长机制;M50NiL钢; 奥氏体; 晶粒长大模型
Abstract
M50NiL steel is the second generation of high-temperature, high-alloy and low-carbon bearing steel which developed on the basis of M50 bearing steel. It is also an alloy steel that is easy to carburize and nitriding. The characteristics of “external hard internal toughness” feature can be obtained through the composite chemical heat treatment process. In addition, due to the residual stress generated in the surface layer after the composite chemical heat treatment, the life of the steel ring as the bearing ring is greatly improved, so it is widely used in aerospace applications. As aerospace components, there are strict requirements on the degree of grain refinement. However, the range of hot forging process of M50NiL steel is narrow, and the grain size of forgings is not easy to control, which may bring many difficulties to actual production. In this paper, the austenite grain growth model of M50NiL steel was studied by heating amp; thermal insulation experiments, and the data was regressed with different models.
Firstly, according to the literatures related to Beck, Hillert and Sellars models, the paper explains the principle of each model, the method of use, and its accuracy analysis process. On this basis, we analyzed the influencing factors and principles that affect the growth of austenite grains in M50NiL steel, and developed a detailed test plan. Then we use the metallographic method to obtain the average grain size of austenite grains of M50NiL steel under different process conditions. We used these three models to study the austenite growth kinetics model with Tempering temperature of 1000℃~1150℃ and holding time of 10min~70min, and studied the advantages and disadvantages of each model. Finally, it was decided to use Sellars model to describe the growth behavior of austenite grains in M50NiL steel. The austenite grain growth kinetic model of M50NiL steel is .
Key Words:Grain growth mechanism;M50NiL steel;Austenite grain;Kinetics models of Grain growth
1 绪论
引言
轴承是支承轴的部件,是现代机器中最广泛应用的部件。航空发动机主轴轴承是发动机中最重要的零部件之一,它的性能好坏对航空发动机的寿命起着决定性的影响。
发动机轴承中的轴承套圈以及滚动体都是由各种轴承钢制得的。因为轴承经常应用在高载荷、高温的工作场合,因此它的性能必须满足这些要求。在生产实际使用中的轴承时,常使用专用的轴承钢,与一般钢种相比,加工后轴承钢的芯部具有较高的塑性和韧性,其表面也需要有高硬度、高耐磨性的特点,这样才能满足日益严苛的工作环境。
现代航空发动机要求有更低的成本、油耗率,更高的耐久性、可靠性,更大的推重比的要求[1,2],这对航空发动机的轴承提出了更高的要求,主要体现在发动机轴承d.n (轴承内径(mm)×转速(r/min))的值变得更大,一般认为d.n值超过的轴承就已经算是高速轴承,而当前服役中的发动机轴承d.n值已经达到了了,在未来的发展目标中,更是要求达到更高的[3]。过高的d.n值将会给轴承的工作带来更大的不利影响,在高速球轴承当中,当d.n值超过一定值时,滚动体不仅将会产生非常大的离心力压向轴承外圈,而且会使外圈应力变化得更加频繁;另外,高d.n值带来的轴承外圈的离心力与滚动体离心力造成的压力甚至有可能使轴承产生破碎性断裂。
在航空航天上,由于更高的d.n值、高的涡轮进口温度和增压比以及更高的飞行器飞行速度,航空发动机中的轴承将会处在长时间较高温度下工作的状态[4]。普通的轴承钢种例如高碳铬轴承钢、渗碳轴承钢、中碳轴承钢以及不锈轴承钢都已经无法满足长时间高温下工作的要求,因为它们在高温下无法保持较高的硬度、较稳定的尺寸、较高的耐高温氧化性和较低的热膨胀性,非常容易在航空发动机中复杂的工况条件下出现失效。
经过大量的试验,一种能在高d.n值、高温下稳定工作的高温轴承钢——M50钢应运而生。此前,M50钢一直是制造航空发动机轴承的专用钢种,然而其疲劳韧性较低、易断裂。在此之后,在M50钢的基础上研究得到了M50NiL钢,较前者而言,M50NiL钢在降低含C量的同时提高了Ni元素的含量,使它的断裂韧性提高了两倍,同时利用表层渗碳工艺,该工艺在提高M50NiL钢的表层硬度、耐磨性之外,还使得材料产生一种从外到内的梯度结构,大大提高了整体的韧性。当前,M50NiL钢是制造航空发动机的主流材料。
关于M50NiL钢的研究
M50NiL钢简介
随着近些年来航空工业的发展,不论是新型战斗机的迭代,还是国产大飞机的研发,都要求航空发动机能在更高的温度和速度下稳定服役更长的时间,发动机主轴轴承在连续工作较长时间的情况下,温度将会超过300℃,而作为M50NiL钢前身的M50钢在这种温度条件下断裂韧性有限,成为了制约航空发动机轴承技术发展的巨大阻碍。上个世纪80年代,在美国海军的支持下,瑞典的SKF公司成功研制了新一代的高温合金轴承钢——M50NiL钢(国内牌号为G13Cr4Mo4Ni4V),与M50钢相比,利用该钢制造的轴承会有更高的断裂韧性。此外,由于其渗碳性能良好,在渗碳工艺处理之后,芯部的强度可以达到M50钢的水平,非常适合在高温、高速的极端条件下工作。
因为M50钢的C含量较高(0.8%),基体组织主要为珠光体,强度硬度高,但是韧性较差。相比之下M50NiL钢中的C含量仅为0.12%,并且加入了3.5%的Ni元素,提高了材料的韧性和强度,而且可以通过复合化学热处理工艺——即在渗碳工艺的基础上进行渗氮处理[5,6],其复合化学热处理过程主要包括以下的工步:工步Ⅰ:真空渗碳,950℃缓冷;工步Ⅱ:真空退火;工步Ⅲ:1100℃真空气淬;工步Ⅳ:-73℃冷处理;540℃回火三次;工步Ⅴ:复合硬化,480℃~500℃气体渗氮。该轴承钢在只经过渗碳工艺处理后,材料的表层会出现高碳马氏体以及弥散分布的合金碳化物,大大提高了表层的耐磨性;在后续的渗碳/渗氮处理过程中,材料在完成渗碳工艺后并不立即进行淬火,而是先进行渗氮处理,最后进行淬火。在M50NiL钢复合化学热处理过程中,因为C、N原子的吸收和扩散导致表层的C、N原子浓度呈现梯度分布,从而产生由表层到芯部组织性能的梯度结构,承载能力更强[7]。另外,在复合化学热处理后表层出现残余应力,该残余应力可以抵消在高d.n值下的圆周力,这也大幅度提高了M50NiL钢轴承的疲劳寿命。
国内外研究现状
伴随航空工业的发展,学者们对M50NiL钢的研究一直都在进行着,也提出了许多能够进一步提高其性能的工艺方法。江志华[7]等人通过研究经过复合化学热处理过程中的M50NiL钢的碳/氮渗层组织性能演变,碳氮原子的吸收和扩散效应使表层的碳氮原子摩尔浓度呈现有层次的梯度分布的状态, 由此得到从表面层到心部组织性能梯度变化,呈现出不同微观结构的界面层;在不同的热处理阶段,不同的界面层由于热处理的响应不同,导致不同的渗层有着不同的演变规律、组织微观结构和硬度性能分布。夏云彤与傅永庆[8]依据一种新的渗层断裂韧性评估方法,分析了氮碳共渗M50NiL钢在不同的回火温度下工件断裂韧性的变化趋势,得出了回火温度越高,M50NiL钢总体的断裂韧性越高的结论;渗氮/碳层残余应力和微观组织组分的梯度变化是造成从表层到芯部断裂韧性升高,断裂机制转变和局部裂纹失稳扩张“Pop-in”形成的主要原因。
P.R. Rios [9]等人利用不可逆热力学(即熵增定理)通过理论计算的方法得到了有钉扎力情况下的正常晶粒生长模型,验证了关于弥散粒子对晶界的作用的齐纳表达式和布鲁克定律都有着良好的热力学基础。S.S.Zhang[10]等人通过实验得到不同工艺(不同加热温度和恒温时间)下的奥氏体平均晶粒尺寸并利用阿伦尼乌斯经验公式得到300M钢的奥氏体晶粒生长模型,其模型的精确度较高,有着良好的预测效果。Kelly[11]研究了M50NiL钢中的M2C碳化物和铁素体之间晶格取向的关系。哈尔滨工业大学的孙湛[12]同学研究了等离子体稀土渗氮和氮碳共渗层组织结构和性能,即稀土元素对复合化学热处理的影响。李红斌[13]等人基于Johnson-Cook模型构建了M50NiL钢的流变应力本构方程。娄艳芝[14]等人应用高分辨电子显微镜(HREM)观察了M50NiL高温渗碳轴承钢中的马氏体和强化相形貌、结构及其与马氏体的取向关系。
奥氏体晶粒生长理论及模型
奥氏体晶粒生长是指材料在尚未产生应力应变时,退火过程中产生的晶粒直径增大的现象[15]。
2.1 晶粒长大原理
参照反应速度动力学的基本原理,纯金属中的晶粒长大可以表示成如下的表达式:
其中,是晶界迁移率,是晶界能,是摩尔体积,是既不长大也不缩小的临界晶粒半径,近似地等于平均晶粒半径[16]。该表达式的实际物理意义是:当第i个晶粒的半径时,,这个晶粒将长大;相反地,时,,这样的晶粒将缩小。式(1)准确地反映了晶粒的长大情况,即大的晶粒通过蚕食周围的晶粒而长大,小的晶粒缩小直至消失,但是这只能反映微观的情况,而求解晶粒半径的统计性分布规律是十分困难的,所以常用简化的波尔克模型[17]:
在这个模型中,我们并不考虑一个个晶粒的长大或缩小,而要关注平均晶粒。根据吉布斯-汤姆逊效应,多晶组织相比单晶组织要多出数量的自由能,而晶粒的长大正是以这部分自由能为驱动力而进行的晶界迁移现象。式中,是多晶组织中晶界的表观迁移率,不同于式(2-1)中的,在一个迁移中的多晶系统中,任何晶粒都与相邻晶粒的公用一部分的晶界,如下图:
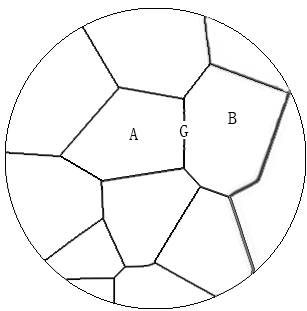
图2-1 晶粒长大机制
上图中A晶粒与B晶粒公用晶界G,若,则在晶粒长大竞争的过程中,B晶粒的长大速率大于A晶粒,晶界G向左侧迁移。这意味着B晶粒的G晶界在迁移过程中受到了来自A晶粒的阻力,因此表观晶界迁移率要小于式 (2-1)中的。Hillert在分析多晶组织的稳态长大时提出了如下的关系式:
在S.Arrhennius和H.Eyring等人倡导的反应动力学中,界面迁移率M有如下的形式:
式中,为适应系数,与激活熵相关;是一个被爱因斯坦称作“原子移动度”的参数;是在晶界迁移过程中原子的跳跃距离。应用到晶粒长大过程中,可以得到晶界迁移率:
式中,是晶界扩散系数,在统计热力学中,它的形式是某一常数与玻尔兹曼因子的乘积;是晶界厚度(对于随机晶界而言可以认为是3个原子间距)。将上面的(2-2)、(2-3)、(2-5)方程整理,可以得到晶粒的平均半径与加热时间t之间的关系式:
式中的是加热之前的的初始值。在实际的钢铁材料中,晶粒的长大速率要比方程(2-6)所描述的慢得多,因为这一长大的过程受到了固溶原子的拖拽作用和弥散粒子的晶界钉扎作用两种阻碍。
因此在实际的生产过程中,Hillert使用了如下的模型来描述晶粒的生长:
我们可以看到,等式(2-6)与等式(2-7)在形式上有着高度的一致性,这从侧面说明了Hillert模型有着严谨的理论基础,等式(2-7)也是我们接下来要使用的模型之一。
2.2 奥氏体晶粒生长动力学模型
预测回火中的奥氏体晶粒生长的动力学模型主要有Beck模型[18]、Hillert模型[19]和Sellars模型[20]。
2.2.1 Beck模型简介
Beck模型最早在研究高纯度金属铝和镁铝合金中的晶粒生长问题时由Beck等人提出,其研究小组在对高纯度金属铝进行了在350℃、400℃、450℃、500℃、550℃、600℃、650℃温度下的退火处理,退火处理的持续时间分别是1分钟、5分钟、25分钟、125分钟、625分钟、3125分钟、15625分钟。将得到的不同热处理条件下的晶粒平均尺寸填入坐标轴对数化的图中,如下图:
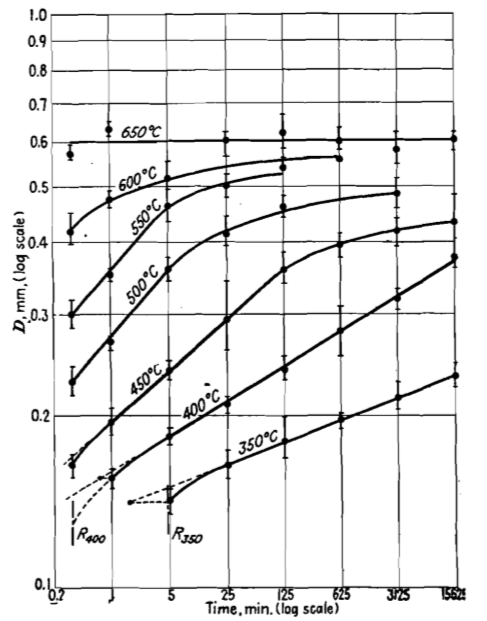
图2-2 Beck实验中高纯度金属铝晶粒生长实验中的对数数据图
上图中,退火温度达到650℃时的D与Time关系是一条水平直线,这意味着在650℃下,晶粒基本上停止了生长。退火温度为600、550、500和450℃的曲线在恒温时间较长时也趋于一条直线,且越来越靠近恒温时间为650℃时的平均晶粒尺寸。他们发现,在热处理工艺过程的前一阶段中,图2-2中在退火温度低于550℃时的直线均存在一定长度的直线部分,说明这一阶段的晶粒生长过程是可以通过一定的关系式来说明的,针对某一温度下的高纯度金属铝的晶粒生长,他们提出了如下的关系式:
式中的D(mm)是经过一定时间t(min)的退火工艺处理后得到的平均晶粒尺寸;K和n在等温过程中是保持不变的常数,不过在不同的温度下会有不同的K和n值。根据图2-2和等式(2-8),显然可以得到如下面的等式:
这个等式是本文线性回归运算的重要基础。
在工件的实际工艺生产过程中,往往没有只存在一个等温过程的工艺,这时我们需要全面地衡量退火工艺中的温度与时间对晶粒生长带来的影响。参数K与温度T符合Arrhenius关系:
对上式两边取对数即可得到用于拟合的线性关系式:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: