摘 要

由于在游戏、建模、VR、电影特效等各种领域中对于计算机真实感渲染需求的不断增加，光线跟踪算法作为一种效果极佳且符合真实物理规律的绘制技术被计算机相关研究人员投入了大量精力进行研究。由于光线追踪算法在真实感模拟的方向具有极高的优越性，因此本文将光线追踪算法与SPH流体模拟方法结合，得到真实的流体模拟效果。基于拉格朗日描述的光滑粒子动力学方法(SPH)擅长于处理自由面剧烈变化的流体现象，因此对于小规模的流体模拟具有极高的真实性。结果表明:该算法可以计算出逼真的流体模拟效果,通过光线追踪算法可以提供场景中物体的深度信息,实现2D图像的三维效果，而SPH方法又可以得到每一帧粒子的准确物理属性与空间位置。这些方法的结合可以在仿真模拟、空气动力模拟、指挥控制及科学计算的可视化等领域都得到广泛应用。

关键词：光线追踪 光滑粒子流体动力学 流体模拟 真实感渲染

Fluid Solver and Renderer Based on SPH

Abstract

Driven by many applications such as games, CAD, virtual reality, and film and television special effects, ray tracing algorithm has been extensively studied as an important realistic rendering technology and vigorously developed. As the ray tracing algorithm has a very high superiority in the field of realistic simulation, this paper combines the ray tracing algorithm with the SPH fluid simulation method to obtain the real fluid simulation effect. The Smooth Particle Dynamics Method (SPH) based on the Lagrange description has its advantage at dealing with fluid phenomena with sharp changes in the free surface, so it is extremely realistic for small-scale fluid simulations. The results show that the algorithm can calculate the realistic fluid simulation effect, and the ray tracing algorithm can provide the depth information of the object in the scene to realize the three-dimensional effect of the 2D image, and the SPH method can obtain the accurate physical properties and space of each frame particle. position. The combination of these methods can be widely used in the fields of simulation, aerodynamic simulation, command and control, and visualization of scientific calculations.

Key Words: Ray tracing; Smoothed particle hydrodynamics; Fluid simulation; Realistic rendering

目录

摘 要 I

Abstract II

第一章 绪论 3

1.1 课题研究背景及意义 3

1.2国内外研究现状 3

第二章 SPH原理 4

2.1 纳维-斯托克斯方程 4

2.1.1 基本方程 4

2.1.2 基本定义介绍 5

2.2 光滑粒子流体动力学 5

2.2.1 SPH基本方法概述 5

2.2.2 流体粒子的物理模型 7

2.2.3压力 8

2.2.4 粘滞力 9

2.2.5 表面张力 10

2.2.6 外力 12

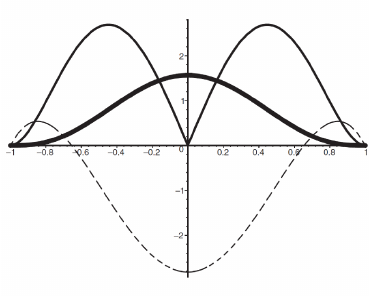
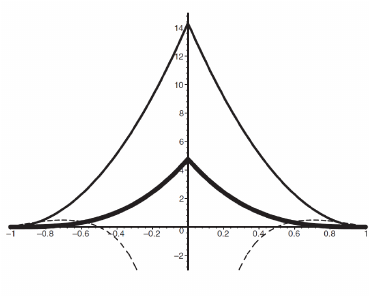
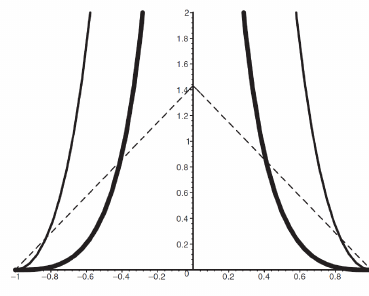
2.3 光滑核函数分析 12

2.4 模拟方式 17

第三章 SPH的实现 18

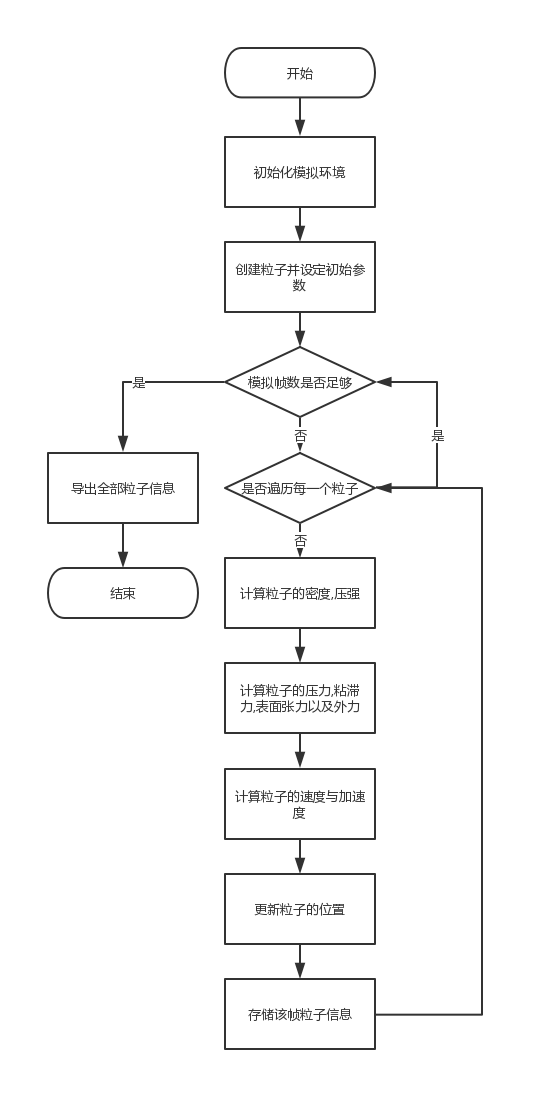
3.1 算法流程 18

3.2 临近粒子搜索 19

3.2.1 全局搜索法 19

3.2.2 空间网格搜索法 20

3.3 粒子内存存储优化 21

第四章 光线追踪算法 21

4.1 光线追踪算法简介 21

4.3 光线追踪算法流程 25

第五章 总结 28

5.1 光线追踪算法 28

5.2 SPH流体模拟 28

参考文献 31

第一章 绪论

1.1 课题研究背景及意义

随着数十年间计算机硬件技术的持续发展以及计算机图形学多个方向中各种算法的不断进步，通过计算机进行各个领域的模拟仿真技术也迅速发展。在电子游戏，影视特效，模拟仿真等各个方面，在图形学技术中出现的各种算法通过不断的相互合作,融合,在各领域得到了日益广泛的运用。但随着技术的发展，各领域对计算机仿真中物体的运动模拟与实时交互效果的真实性提出了更高的要求。由于真实世界的物体运动常常难以严谨描述，因此通过借助真实世界的物理规律进行实现变成了一个简单有效的方法。由于流体模拟作为计算流体力学与计算机图形学交叉的研究热点，在近年出现了许多的进步与改进，因此在电影动画，电子游戏与特效等方面有着吩咐的运用。由于真实世界中水流规律的复杂性，运用物理规律进行流体模拟是一项艰难的工作。当前主流的流体模拟有多种方式，但在目前主流研究中的存在两种主要的模拟方法：欧拉法和拉格朗日(粒子)法。欧拉方法使用空间域的细分来控制问题，并控制每个网格中的流体流动。这些技术已经能够实现最简单的液体类型模拟，从简单流动到高粘性流体，以及具有塑性和弹性行为的液体。通过这种方法模拟能够方便的执行强制执行不可压缩条件，但不能保证质量守恒。拉格朗日方法将研究的流体模型离散化为单个粒子，通过跟踪研究粒子在系统中运动时从头到尾空间位置的变化，直接追踪每一个单个粒子，该法可以简单地保证质量守恒并提供简单和通用的模拟框架。拉格朗日粒子法还减轻了对特定参考系的依赖性。在欧拉方法中，流体特征在模拟期间可以改变的距离受到网格细化程度的限制。因此，对于非常快速和微观的流动，追踪在空间中的固定点处发生的变化似乎不如直接沿着粒子轨迹发生的变化进行观察。粒子模拟的一个重要缺点是难以用粒子表示光滑表面。稳定地处理少量液体形成的小特征的表面张力效应也是一项艰巨的任务。表面张力是小范围液体最为明显且常见的物理特性。表面张力只存在于流体表面的液体分子间，其力的大小取决于不同液体表面的曲率。从微观的角度来看，流体中各个粒子受到其他周围粒子来自不同方向的作用力，这些作用力根据液体间不同的。

1.2国内外研究现状

由于现代GPU的快速发展，借助GPU的硬件特效来进行并行计算逐渐在各个领域得到发挥出了其独特的优势。在计算机图形领域，对于流体的模拟与真实感渲染的越来越高的需求，使用GPU并行算法已经成为一种主流的加速方式。而现阶段的流体模拟主要方向为使用光滑流体粒子动力学的算法，将流体粒子化，从而以拉格朗日视角对微观流体进行模拟。该方法将流体离散为具有多种物理属性的单独粒子来研究，结合不同的时间迭代算法，求解N-S方程，得到下一个时间点所有粒子的位置，密度等状态。再通过卷积的思想，使用不同的光滑和函数对核半径内所有粒子的属性进行加权得到自生的属性。光滑流体力学方法首先被用于模拟大范围的星际间气体的运动。再2013年首先由Muller等人第一次将该方法引入计算机图形学领域用于流体模拟。但是由于Muller等人的方法未对流体的体积守恒进行约束，因此在流体模拟时的不可压缩性问题并没有得到解决。由于光滑流体力学的方法在模拟流体时，每一个粒子的质量较低，在模拟时难以保证数值的稳定性。为了解决该问题，Becker等人在2007年使用Tait方程对该方法进行优化，实现了弱可压SPH。但是该方法为了维持流体的稳定性，在模拟时的时间步长必须缩短到微秒级别，使得需要模拟的时间非常长，模拟的进程十分缓慢。为了结局该问题，Soolenthaler与Pajarola两人于2009年提出了预测矫正不可压缩性SPH(PCISPH)，该方法有效的解决了在均匀密度流体模拟中，不可压缩的约束并且将模拟的步长提升到毫秒级别。在本文中运用的流体模拟方法为Muller等人提出的SPH算法，并且使用GPU并行计算的方式将串行算法迁移为并行算法，并提出了多种并行算法的实现。

第二章 SPH原理

本章描述了基于流体动力学原理中光滑粒子流体动力学算法的基本原理与核心思想。并给出了该算法中设计的多个物理公式以及相关算子的推导公式。该章阐述的物理原理为后续的代码实现提供了理论基础，使模型的实现更贴近真实效果。

2.1 纳维-斯托克斯方程

2.1.1 基本方程

本文在计算流体粒子属性时基于纳维-斯托克斯方程(N-S方程)的基本物理原理。该方程在18世纪由纳维与欧拉提出，最初被称为欧拉方程，后经过柯西，泊松等人的修改与优化得到了现在的最终的形式。

2.1.2 基本定义介绍

本节对该文章公式推导过程中所用到的一些多元微分知识进行简单的说明与介绍，包括标量场，矢量场，Hamiltonian算子，Laplace算子，散度，旋度。

标量场 标量场(Scalar Field)是数学定义中的场。假设在某个空间中的某一点可以采用一个标量来表示其某种属性，则该场被称为标量场。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：