空心矩形截面高墩承载力分析毕业论文
2020-02-19 16:29:18
摘 要
随着社会的不断发展,我国的道路桥梁建设事业不断的发展,规模日渐增大,桥梁的研究水平也在不断提高。高墩桥梁由于自身的独特优势,在国内被广泛的应用。为了节约材料的用量并减轻桥梁的自重,许多高墩通常被设计成空心墩,这就体现了对于空心截面桥墩的承载能力的研究的重要性。
本文首先根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》中给出的方法来分析空心矩形截面高墩的承载力,然后以长虫沟大桥P7桥墩的左幅桥墩为工程实例背景,基于OpenSees软件,对该桥墩进行了有限元分析,得到该结构的极限承载能力,然后改变不同的参数,做出P-M曲线并进行分析。分析表明,混凝土强度等级以及纵筋的配筋率是影响空心矩形截面高墩的承载能力的重要因素。
之后使用图算法,根据不同的配筋率和混凝土的强度等级,确定不同的强度配筋率,根据不同的组合,画出m-n曲线,完成了量纲为1的轴力-弯矩曲线诺模图,该图计算简单快捷,大大方便了工程设计中的计算,通过查图的方式便可以进行设计。
关键词:空心矩形截面;极限承载力;OpenSees;P-M曲线分析;图算法
Abstract
With the continuous development of society, China's road and bridge construction industry continues to develop and its scale is increasing, the research level of bridges is also constantly improving. Due to its unique advantages, the high pier bridge is widely used in China. In order to save material usage and reduce the weight of the bridge, many high piers are usually designed as hollow piers. This embodies the importance of the study of the bearing capacity of hollow section piers.
This paper first analyzes the bearing capacity of hollow rectangular section high piers according to the method given in "Design Specification for Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts". Then take the left span of the P7 pier of Changchonggou Bridge as the engineering example background. Based on OpenSees software, the finite element analysis of the pier is carried out, and the ultimate bearing capacity of the structure is obtained. Then change the different parameters, make a P-M curve and analyze it. The analysis shows that the concrete strength grade and the reinforcement ratio of the longitudinal reinforcement are important factors affecting the bearing capacity of the hollow rectangular section high pier.
Then use the graph algorithm, according to different reinforcement ratios and concrete strength grades, different strength reinforcement ratios are determined. According to different combinations, draw the m-n curve and complete the axial force-moment curve with dimension 1 of Nomogram. The calculation of the figure is simple and fast, which greatly facilitates the calculation in the engineering design, and can be designed by means of the inspection.
Key words: hollow rectangular section; ultimate bearing capacity;OpenSees; P-M curve analysis; graph algorithm
目录
第一章 绪论 1
1.1课题的研究背景及意义 1
1.2 RC空心矩形截面桥墩的研究现状及应用 2
1.2.1 RC空心矩形桥墩的应用 2
1.2.2 RC空心矩形截面桥墩研究现状 2
1.3本文的主要研究内容 4
第二章 空心矩形截面承载力计算理论 7
2.1基本假定 7
2.2计算公式及其使用情况 8
2.3等效钢带法 12
第三章 基于OpenSees软件建立桥墩有限元分析模型 14
3.1有限元分析程序OpenSees简介 14
3.2实例简介 15
3.3参数取值 16
3.4模型建立 17
3.4.1纤维模型简介 17
3.4.2 材料的本构关系 17
3.4.3节点与截面的建立 18
第四章 桥墩承载能力分析 22
4.1相同材料和截面尺寸以及配筋的偏压构件P-M关系曲线分析 22
4.1.1大偏心受压情况 22
4.1.2 小偏心受压情况 23
4.1.3通过模型分析P-M曲线 24
4.2相同截面尺寸,材料,不同配筋的关系曲线 26
4.2.1 P-M曲线绘制 27
4.3 P-M关系曲线分析 29
第五章 图算法分析承载力 31
5.1 图形的绘制 31
5.1.1 强度配筋率不变的m-n曲线 31
5.2实例应用 35
5.2.1算例 37
5.2.2 结果分析 39
5.3 小结 39
第六章 结语 40
6.1主要完成的工作 40
6.2主要结论 40
6.3展望 41
参考文献 42
附录:OpenSees命令流 44
致谢 48
第一章 绪论
1.1课题的研究背景及意义
桥梁在社会经济中拥有着十分重要的作用,桥梁也是陆路运输的必要节点。此外,桥梁不仅在交通网络中占有非常重要的作用和地位;另外,在特殊时期,对于解放军部队的流动有着重要作用。自近代以来,中国桥梁建设的发展实现了跨越式发展。截至2012年,我国已经分别建成了71.3万座公路桥梁以及5.8万座的城市桥梁,如此多的桥梁使中国成功进入世界桥梁大国的行列。
近年来,我国的桥梁建设事业大规模发展,对桥梁的各个方面的研究不断提高。高墩桥梁由于其自身的适应地形等独特的优势,在国内被广泛应用。我国西部地区已经建成了大量的高墩大跨径连续桥梁,而且同类的桥梁数量愈来愈多,而且由于我国地形复杂多变,同时也为了节约材料和减轻自重,许多高墩常常被设计成空心墩。目前我国高墩桥梁愈来愈多,因为施工等因素的影响,它的稳定就变得十分重要,国内外曾经发生过不少因为失稳而导致的事故。这就体现了空心墩承载能力的研究的重要性。
空心矩形截面钢筋混凝土桥墩有着较高的强度质量比以及相当的刚度质量比,还有这良好的延性能力,这种桥墩不仅减小了桥墩的质量,而且使结构发挥了其自身的最大效益。因此空心矩形截面的桥墩在中国的高墩桥梁种的到广泛的应用。而且高墩桥梁的施工安全和其极限承载能力已经引起了广大桥梁工作者的重视。因此对该种桥墩的极限承载能力的研究,对于保证同类的高墩桥梁的结构安全以及使用安全、完善桥梁设计施工技术都具有重要的显示意义和工程使用意义。
1.2 RC空心矩形截面桥墩的研究现状及应用
1.2.1 RC空心矩形桥墩的应用
空心矩形截面桥墩具有较大的刚度质量比以及强度质量比,可以较大的减小此种桥墩的钢筋混凝土的用量,而且该种桥梁较为经济还能发挥桥墩的最大效益,因此在高墩桥梁中,RC空心截面桥墩所占比重很大,尤其是我国西部的高地震烈度区域,空心矩形截面高墩桥梁在该地区有着广泛的应用。例如:王俊杰等人[1]对1960年至1980年之间建设的155000个桥墩进行了研究,得出以下结论:随着墩高的增大,空心矩形截面桥墩应用越多,而且墩高在100米以上的桥墩,大部分使用空心截面形式。贵州省打见河大桥的桥墩结构形式为箱形截面薄壁桥墩;罗甸县境内的八来河茂井大桥,该桥的1、2号桥墩均为 6.5米×6.5m米的混凝土薄壁空心墩。孙治国等人[2],研究并统计了国内的已建的铁路桥梁中的35个铁路桥梁的空心桥墩,还有大型公路桥梁中的97个空心截面桥墩的建设情况,通过他的研究可以知道,其中公路桥梁空心桥墩均为空心矩形截面,我国的公路桥梁所有桥墩一般都为空心桥墩,而且在横桥方向剪跨比都大于10,而且都是空心矩形截面形式的高墩。
1.2.2 RC空心矩形截面桥墩研究现状
我国山河众多,各地的地理环境较为复杂,改革开放以来公路桥梁以及铁路桥梁的建设突飞猛进。因此提高桥梁的承载能力安全以及研究桥梁的抗震性能十分重要。由于空心矩形截面桥墩不仅拥有良好的受力性能以及抗震性能,所以空心矩形截面桥墩在道路桥梁建设中得到广泛的应用。
崔海琴等[3][4],采用低周反复荷载试验方法,设计了4个空心矩形薄壁桥墩和5个在塑性铰区域加碳纤维约束的空心矩形薄壁桥墩模型,使用该种模型研究影响空心矩形截面薄壁桥墩的抗震性能的因素。试验表明:影响桥墩延性性能的主要因素是结构的体积配箍率,箍筋不仅可以显著提高试件的延性能力还可以提高试件的耗能能力,随着配箍率的增加,试件的位移延性系数渐渐开始增大;增大轴压比,构件的承载能力有所降低,进入屈服阶段后,变形能力逐渐减小,抗震性能越来越差。
孙治国和王东升等人[5]对矩形空心墩的变形能力进行了研究,通过在塑性铰区域配置不同数量的约束箍筋和纵筋,发现影响矩形空心墩变形能力的主要因素是塑性铰区配筋率,以及纵向配筋率,壁厚和轴压比,研究发现矩形空心墩变形能力随着体积配筋率、纵向配筋率和壁厚的增加而增加,随着轴压比的增加而减小。
Yasuyuki等[6],对空心矩形截面高墩进行了研究,通过设计15个比例为1:10,且纵筋布置与真是桥墩相似的桥墩模型,并且用其进行了低周反复荷载试验。通过上述试验对箍筋率、墩底截面形式、剪跨比以及扭转效应等因素对抗震性能的影响进行了大量研究,研究结果表明,箍筋是影响抗震性能的主要因素,可以通过改变横向箍筋的不知来提高桥墩的延性性能,合理的布置对延性性能的影响比较大,并且提出了箍筋布置与延性性能之间的关系。
Paolino Cassese等人[7],对不同长宽比的空心矩形RC墩进行了研究,针对四个试样,在具有恒定轴向荷载的位移控制下进行循环测试。考虑到横截面和加固的细节,根据试样的高度和加载方向考虑不同的长宽比。根据长宽比,预计会出现不同的失效模式,即弯曲高墩失效和短墩弯矩屈服后出现剪切破坏。
Nahid Attarchian等人[8],通过对6个 不同的方形和矩形空心截面的RC悬臂柱进行了研究。考虑到了形状,长宽比,尺寸,轴向压力,混凝土特征强度和纵向配筋率的变化。然后开发出一种新的方法来评估双轴压弯下的空心矩形截面桥墩的延性能力。
Fatemeh Shirmohammadi等人[9],通过建立基于光纤的模型来进行模拟RC柱的变形,考虑了弯曲强度、延性、能量消耗、以及加载路径等因素,然后研究轴向荷载对柱的单轴和双轴性能的影响。证明了在单轴横向位移下,增加轴向力会导致柱的单个循环和累计消耗能量的增加。在双轴横向位移下,该柱没有这种趋势。
国内外对RC矩形截面问题进行了较多研究,研究方法主要为拟静力试验或试验与数值模拟相结合,也有少量文献采用了纯数值模拟的方法。
试验和数值模拟结果表明,在轴心压力的作用下,RC矩形空心截面桥墩在侧向力的作用下的破坏过程如下:桥墩的保护层混凝土产生裂缝,接着桥墩底部附近混凝土开裂,纵向钢筋屈服;桥墩底部4个角位置处的混凝土剥落,核心区混凝土在外力的作用下被压碎;最后桥墩混凝土被压碎,内部纵向受力钢筋发生屈服。对于RC空心矩形截面桥墩的破坏形式,试件的长细比对破坏影响较大:空心矩形截面的高墩的破坏形式均为破坏;若降低试件的长细比,则剪切效应的影响将会变大。
研究显示,影响RC空心矩形截面桥墩的承载性能的因素有:(1)轴压比;(2)长细比;(3)纵向率;(4)横向率;(5)钢筋强度。
此外,在单轴压弯和双轴作用下,RC矩形空心截面墩的抗震性能不同[10]。许紫刚等人对于实际桥墩在和双向下的曲线进行的计算是按照《公路桥梁抗震设计细则》来进行计算的,计算结果表明:截面设计时,如果只考虑单轴压弯的情况,那么截面的设计偏于不安全,除此之外当在试件截面上施加双轴压弯时会降低截面的承载力。
1.3本文的主要研究内容
第一,介绍有关空心矩形截面高墩承载力理论,并讨论其优缺点。根据规范按照要求进行各种情况的计算。
第二,说明模型的基本概念以及建立方法,利用有限元分析软件OpenSEES进行模型的建立,然后根据公式手算验证所建立模型是否正确。
第三,针对一个空心矩形截面高墩承载力计算实例,建模完成后,针对不同的配筋情况,做出不同情况情况下的P-M曲线如图,然后利用P-M曲线进行承载力分析。
第四,通过图算法,根据不同的配筋和不同强度等级的混凝土,得到不同的强度配筋率,然后通过OpenSees软件电算,画出量纲为1的m-n曲线诺模图,为简化工程设计中的计算,提出一种简单快捷的设计方法。以该量纲为1的m-n曲线诺模图,在进行工程设计时,通过查图即可进行简单的设计。
以下以一个简单的图示来介绍本文的研究路线:
极限压应变理论
计算方法
空心矩形截面高墩承载能力分析
模型简介
模型建立
桥墩实例
验算模型正确性
OpenSees电算
做出P-M曲线
承载能力分析
不同等级混凝土
不同强度配筋率
不同配筋
m-n诺模图
图算法
第二章 空心矩形截面承载力计算理论
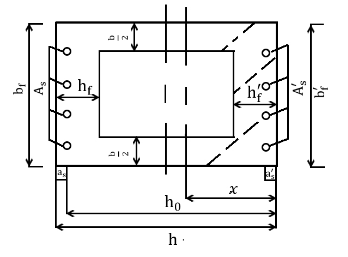
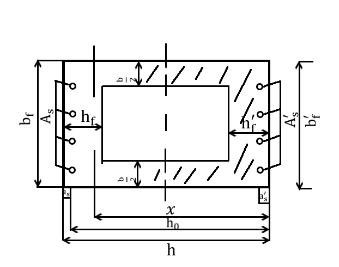
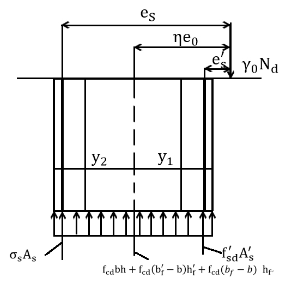
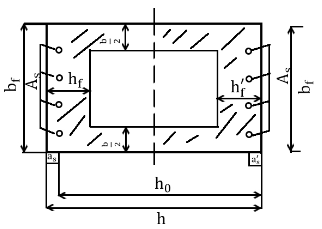
本文根据《公路及预应力设计规范》(JTG D62 - 2018)[13](以下简称 《公路桥规》),以及《结构设计原理》[14]中所给出的正截面的计算公式进行计算。通过对空心矩形截面受力分析可以得知,偏心受压情况下的空心矩形截面的计算与T形截面构件较为相似,所以根据等效原则,将空心矩形截面换算成T形截面,以下给出该T形截面的正截面的承载力计算公式以及使用情况。
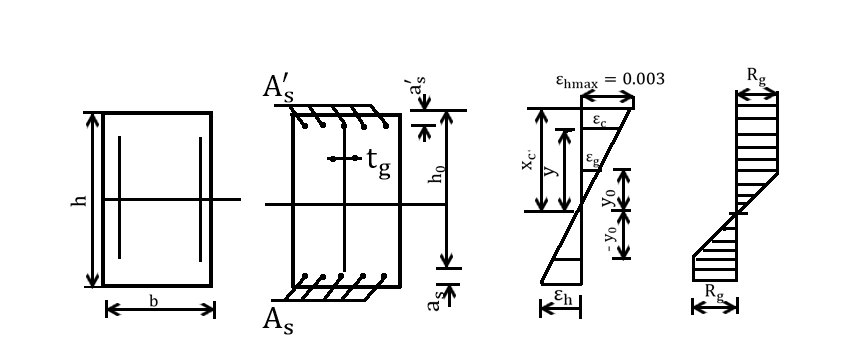
2.1基本假定
在的基础上,根据《公路桥规》的规定,根据以下假定来进行RC矩形空心截面的正承载力:
- 构件截面的弯曲变化情况应该符合平截面假设;
- 对于构件截面的受拉区域的混凝土不考虑其抗拉强度,所有拉力全部由混凝土内的纵向受力钢筋承担;
- 在混凝土达到承载能力极限时,受压区混凝土达到抗压强度设计值矩形应力图计算,应力图的高度为x;在受压较大边钢筋的应力取钢筋抗压强度的值。
- ,,在屈服之后钢筋应理想的;
- 截面受拉边缘或者受压较小边缘的钢筋的应力取值方法,应该按照《公路桥规》的规定取值:
当构件属于大偏心受压时,即时,;
当构件属于小偏心受压情况时,即时,按照以下公式进行计算:
,
式中的——为第i层纵向钢筋受力,为拉应力时计算结果为正,否则为负;
——混凝土的极限压应变,  ,取=0.0033;
,取=0.0033; 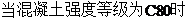 ,取=0.003;C50-C80之间用直线插入法计算;
,取=0.003;C50-C80之间用直线插入法计算;
——钢筋的杨氏模量;
——截面受压区应力图高度系数,混凝土等级C50及以下时,取=0.8;C80时,取=0.74,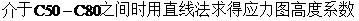 ;
;
——第i层纵向钢筋重心到受压区边缘距离;
X——截面受压区高度。
2.2计算公式及其使用情况
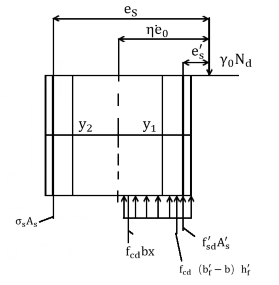
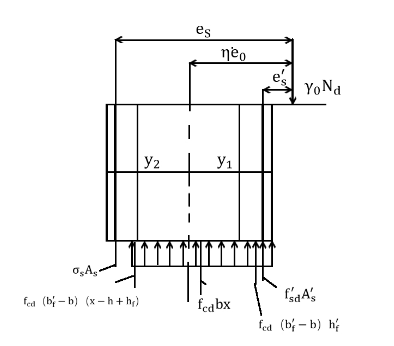
根据截面中性轴的所处的不同位置,划分为以下情况:
(1)当中性轴在截面的受压翼缘内时,即,如图2.2.1所示。此时混凝土正力算方法同宽度为的矩形偏心受压构件。公式即以下所示:
由得: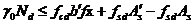 (2.1)
(2.1)
由=0得: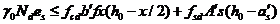 (2.2)
(2.2)
由得: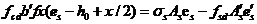 (2.3)
(2.3)
此时为大偏心受压构件,取。公式需要满足条件:。
若不满足上述条件,则取,又因为,所以正截面承载力计算公式为: 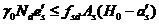 (2.4)
(2.4)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: