基于熵理论的轴承振动信号故障诊断毕业论文
2020-02-17 22:26:17
摘 要
轴承是转动机械中一类常用零器件,在工业生产生活中有至关重要的作用。轴承作为一类精密零器件,其损伤会带来更严重的机械生产事故。对轴承的故障检测能有效避免损失。本文主要对轴承数据进行分析,运用信号处理的手段进行故障识别,确定故障发生位置。
针对轴承早期故障较难排除的问题,本文在熵理论的基础上对轴承进行故障识别。在标准轴承数据库中提取数据,将整理的数据分类为训练组及测试组。针对轴承振动信号不规则的特点,对各组数据进行变分模态分解得到若干模式。为得到的每个模式计算其排列熵值。将训练组排列熵值作为特征向量输入支持向量机训练器中进行训练,将测试组排列熵值输入分类器进行分类,检验轴承故障识别效果。
通过MATLAB对轴承数据库数据的仿真处理表明,该方案具有较高的准确度,有较大的实用性及可行性,对噪声的鲁棒性较好。
关键词:排列熵;变分模态分解;故障识别,支持向量机。
Abstract
Bearing is a kind of common parts in rotating machinery, which plays a vital role in industrial production and life. Bearing is a kind of precision parts, its damage will bring more serious mechanical production accidents. The bearing fault detection can effectively avoid the loss. In this paper, bearing data are analyzed, fault identification is carried out by means of signal processing, and fault location is determined.
In view of the difficulty of eliminating the early fault of bearing, this paper identifies the fault of bearing based on the entropy theory. Data are extracted from standard bearing database and classified into training group and testing group. In view of the irregular characteristics of bearing vibration signals, several modes are obtained by variational mode decomposition of each group of data. The permutation entropy of each pattern is calculated. The training group permutation entropy values are input of the support vector machine trainer as eigenvectors for training, and the test group permutation entropy values are input of the classifier for classification to verify the bearing fault recognition effect.
The simulation processing of bearing database data by MATLAB shows that the scheme has higher accuracy, greater practicability and feasibility, and better robustness to noise.
Keywords: permutation entropy; variational mode decomposition; fault identification; support vector machine.
目 录
第一章 绪论 1
1.1 研究背景及意义 1
1.2 滚动轴承故障识别方法概述及国内外研究现状 1
1.2.1 发展历程 1
1.2.2 滚动轴承故障识别方法 2
1.2.3 滚动轴承故障识别国内外研究现状 2
1.3 论文组织结构 3
第二章 轴承信号处理方法 4
2.1 信号分解的基本方法 4
2.2 变分模态分解的理论基础 5
2.2.1 维纳滤波器 5
2.2.2 希尔伯特变换 5
2.2.3 混频原理 6
2.3 变分模态分解的实现 6
2.3.1 变分模态分解的数学原理 6
2.3.2 变分模态分解流程 7
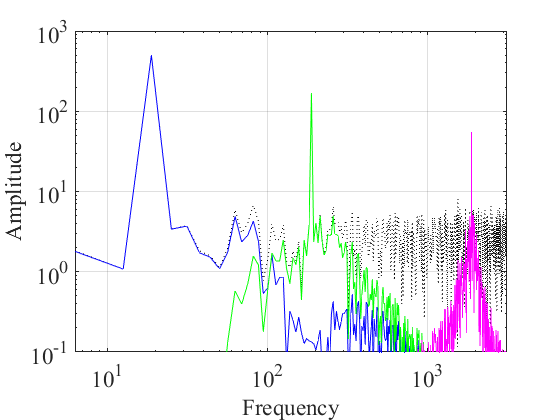
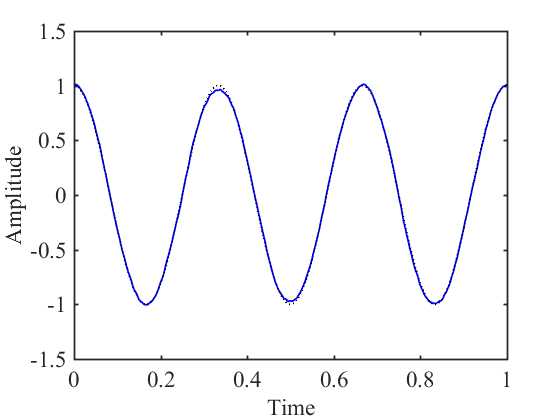
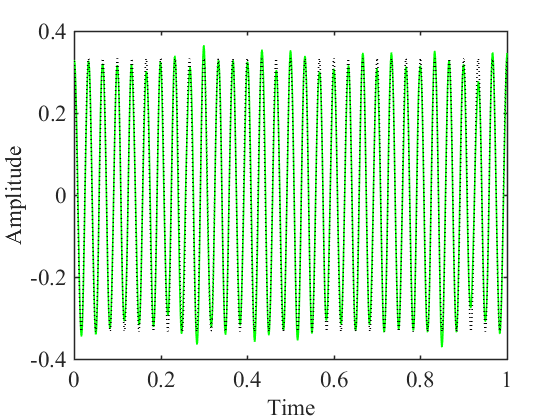
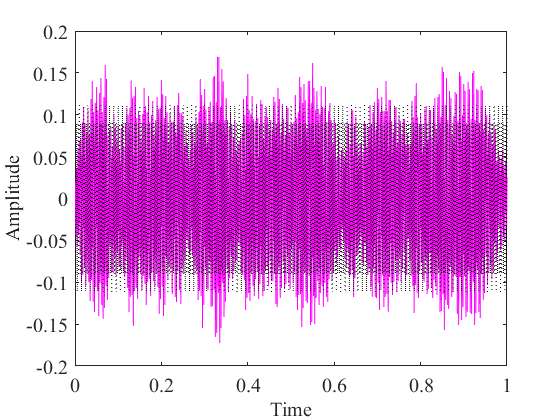
2.4 变分模态分解仿真 8
2.5 时间序列复杂度表征 10
2.5.1 时间序列复杂度表征方法 10
2.5.2 排列熵数学原理 11
2.6 支持向量机 12
2.6.1 支持向量机基本原理 12
2.6.2 SVM的核函数 12
2.6.3 软间隔支持向量机 13
2.6.4 多分类问题上的扩展 13
第三章 轴承故障识别 15
3.1 信号模式分解 15
3.1.1 模式数的确定 15
3.1.2 惩罚参数α的选取 19
3.2 排列熵参数 19
3.2.1 阶数 19
3.2.2 延时 20
3.2.3 数据长度 20
3.3 故障特征提取流程 21
3.4 故障识别测试 22
3.4.1 测试前准备工作 22
3.4.2 无噪声下轴承故障识别测试 22
3.4.3 有噪环境下轴承故障识别 24
3.4.4 训练样本与测试样本比例对识别的影响 27
3.4.5 训练与测试组数对识别的影响 28
第四章 总结与展望 30
4.1 全文工作总结 30
4.2 尚待优化的目标 30
4.3 研究展望 30
第一章 绪论
研究背景及意义
轴承是机械设备中一类应用十分广泛的零器件,能起到支撑转动部件以及减少摩擦等关键作用。滚动轴承具有对润滑剂黏度不敏感,可替代,易于批量生产等优良特性。然而,滚动轴承却也容易损坏。常见的滚动轴承故障包括疲劳剥落,塑性变形,裂纹或断裂,保持架损伤,磨损,锈蚀或电蚀,烧伤及胶合等[1]。
由轴承故障可以引发相关次生反应,致使机械设备损坏或停止运转,造成更大的经济损失及安全事故。可以想象,如果在生产生活中可以实时监测评估轴承工作状态,识别轴承是否发生机械故障,进一步确定故障发生位置及故障损伤程度,将为生产维修提供明确的工作方向,极大地降低二次事故的发生率,从源头减少经济损失。
随着信号处理技术的发展,各种对复杂信号的分析也日益完善。虽然国内外专家学者在机械故障识别这一块已做过大量研究,取得了很多不错的成果,但受复杂生产环境及各种不确定生产因素的影响,在实际的故障检测及识别中往往没有一个固定且可靠的模式。本文依此提出一种基于熵处理的识别方法,该方法适用范围较广,实施相对简捷,识别正确率较高。经测试,该方法对滚动轴承内圈,外圈及滚动体的故障判断准确度很高,有一定的应用及推广价值。
滚动轴承故障识别方法概述及国内外研究现状
发展历程
滚动轴承故障检测与识别的技术由来已久。概括来说,可将其分为四个阶段[2]:
第一阶段始于1960年,随着快速傅里叶变换技术的产生与推广,频谱分析开始在信号分析中扮演重要角色。这一阶段主要将滚动轴承的故障识别与频谱分析仪结合起来,通过频域分析来识别区别正常信号与故障信号。可是受限于环境噪声及高昂的设备价格,该阶段的试验并没能取得很好的效果。
第二阶段发生在1970年左右,与冲击脉冲计的发明息息相关。运用冲击脉冲技术进行的故障识别效果要比频谱仪好,随着这一技术的不断更新完善,其应用领域也不断扩展。
第三阶段可以认为始于1974年共振解调分析系统的问世,这一系统既有对冲击脉冲的幅值检测,又包含信号的频谱分析,对轴承的故障识别颇有效果。
第四阶段在1980年以后,以微机系统为处理中心来进行滚动轴承的状态监测与故障识别,随着算法的改进及机器运算速度的提升,滚动轴承故障识别的收效越来越好。
滚动轴承故障识别方法
故障识别是机械生产中一个重要课题,其方法也多种多样,这里列出几种常用的故障识别方法[3][4]。
- 油液检测法:这种方法对轴承损坏的识别是通过对油样成分的光谱/铁谱分析或油液的黏度变化来实现的。但该方法不适用于脂润滑轴承。
- 温度监测法:温度监测法主要针对轴承座处的温度进行实时监测,然而一些轻微故障并不能造成温度的明显变化,因而其适用范围较窄。
- 声发射法:声发射法利用超声波信号产生声发射现象,依据周期判断故障发生位置,效果不错,但其设备造价较高。
- 振动分析法:振动分析法应用最多。它通过安装在轴承适当位置的传感器采集轴承振动信号,通过对其分析处理识别轴承故障。本文即采用此方法。
滚动轴承故障识别国内外研究现状
现如今轴承振动信号的故障识别方法已经由一开始的时域分析,频域分析转为时频域分析。
经验模式分解(Empirical Mode Decomposition,EMD)是自适应分解信号的常用方法[5]。赵志宏等人在此基础上提出了一种基于样本熵的轴承故障诊断方法[6],张淑清等则提出一种基于互近似熵和掩蔽经验模式分解的轴承故障诊断方法[7]。这些方法的共同点是,在对信号做进一步的处理前,先对信号进行基于EMD或改进EMD的分解。在郑小霞等人的研究中,提出了基于变分模态分解的识别方式[8]。郑小霞认为,变分模态分解在处理这一问题上是优于经验模式分解的。在郑近德等人的研究中,指出可以使用改进的多尺度模糊熵来对故障信号进行诊断[9],识别方法采用支持向量机(Support Vector Machine,SVM)。
国外方面,Juhamatti Saari等提出了用支持向量机检测和诊断风车轴承故障的方法[10],Gustavo等提出了基于熵理论的早期轴承故障诊断方法[11],在这一领域,国内外研究差距不大。
关于轴承故障检测及识别,国内外研究已趋于成熟。在关于轴承振动信号的检测方法中,提取信息阶段中大多使用EMD及其改进方法,以及功能更为完善的LMD(Local Mean Decomposition,局部均值分解)和VMD(Variational Mode Decomposition,变分模态分解)方法。在熵的选择上则更为广泛,包括近似熵,模糊熵,排列熵,样本熵,能量熵,尺度熵,各类谱熵等均可使用。在信号的识别辨别方面,则可使用SVM,FCM(Fuzzy C-means Algorithm,模糊C均值聚类),K-均值聚类等多种方法。
论文组织结构
本文通过变分模态分解滚动轴承振动信号。得到的本征模态分量计算其排列熵值,最后用支持向量机帮助识别故障位置,有一定的实用价值。本文组织结构如下。
第一章主要介绍了设计的背景及意义,描述了课题发展历程,常用方法及国内外研究现状。
第二章讲解了变分模态分解的基本理论及仿真分析,描述了变分模态分解的一些基本特性。介绍了排列熵的基本理论,展示了其在信号处理复杂度表征方面的作用。描述了支持向量机的有关知识。
第三章在MATLAB下仿真模拟了轴承振动信号数据的VMD及排列熵处理,确定了模式个数,计算了各模式的排列熵值,观察其基本特征。实现了支持向量机对轴承故障的识别及分类工作,得出实验的准确率,验证算法效果及可行性,着重探讨了噪声对识别的影响。
第四章主要对本课题进行了总结和展望,提出一些尚待优化的问题。
第二章 轴承信号处理方法
对滚动轴承振动信号这一类复杂信号而言,需用相应的非平稳信号处理办法进行处理。为了从复杂的信号中提取能够表现信号特征,且方便进行数学计算的成分,需要对信号进行分解。信号分解的目标是得到一系列含有信号特征且相对独立的子信号。在得到子信号后,为了方便进行数学处理,为每个子信号序列计算其时间复杂度。如此,便可将一复杂信号用简单的几个数学量来表征。将信号的表征量输入SVM进行训练学习,最后完成轴承状态的识别工作。
2.1 信号分解的基本方法
对复杂信号的分解问题由来已久。最开始人们在时域对信号进行分析,对于连续或离散的平稳线性信号取得了一些成果。在傅里叶变换提出之后,人们开始着眼于在频域对信号进行更好的解析,由此衍生出连续域的拉普拉斯变换和离散域的Z变换,大大提升了信号处理的能力。后来人们发现在单一时域或频域分析可能还是不能解决问题,因而提出时频域分析方法。
对于轴承振动信号而言,其本身的信号特征决定了常规的时域或频域方法均不适用。常用的信号分析方法,往往不具备自适应的特性,在求解相关问题可能会遇到麻烦。具体来说,短时傅里叶变换无法兼顾时间分辨率与频率分辨率;Winger-Ville分布则对固有交叉干扰项较为敏感;小波变换有着预先确定小波基函数的限制[7]。
一种有效的解决方法是采用Huang等人提出的EMD[5]方法。EMD能将信号分解为若干本征模式函数(Intrinsic Mode Function,IMF)。EMD着眼于瞬时频率,以其来作为信号交变成分的表征。往往研究者只关心那些可以表征信号的几个IMF分量而忽视其它分量。在EMD中定义的IMF是其原始定义,即IMF信号必须满足:
- 在整个定义范围内,函数(时间序列)的极值点与零点数量之差不大于1。
- 函数(局部序列)上的任意一点,其局部极大值与极小值所确立的上下包络的均值为0。
之所以说EMD可用于分解任意信号,是因为Huang等假设信号都可以看成是一系列IMF的组合。EMD通过反复在原信号中去除上下包络均值,直到得到IMF。在得到一个IMF分量后,就将其从原信号中抽离出来,再对剩下的信号重复上述步骤。这样,直到最后所余分量对研究问题影响不大或变成单调函数,这时便停止迭代。
但这样定义的EMD其缺点也是明显的。由于EMD的分解与极值点分布相关,且极值点可能存在于信号端点处,在拟合时难以确定包络线的走势,因而可能会存在端点效应。同时,EMD在分解时可能会出现其中若干个时间尺度的IMF不连续,导致一个IMF由多个不同信号组成,抑或是同一尺度信号存在于不同的IMF分量中,产生模态混叠。
与上述方法不同,Dragomiretskiy K等提出的变分模态分解[12]方法,重新定义了本征模式函数,将其用调幅调频信号表示。VMD方法提出每个IMF分量均具有有限带宽,且中心频率各不相同的假设。基于此,VMD尝试找出这样一种分解方式,使得各本征模式函数的估计带宽之和最小。相比于EMD方法而言,VMD方法在信号分离方面往往效果更佳,由于更改了IMF的定义,因而也有效的处理了模态混叠和端点效应的问题。本设计即采用这种方法。
2.2 变分模态分解的理论基础
VMD旨在找出一种模式组合和它们相对的中心频率。VMD与维纳窗滤波降噪有强烈的相关性。事实上,该模型是传统维纳滤波在多频带,自适应频带方面的延伸拓展,为分解问题提供了一种有着坚实理论基础且易于理解的解决方法。该变分模型通过使用多路径的交替方向法来有效的找出最优化解。
变分模态分解主要基于维纳滤波器,希尔伯特变换和混频原理[12]。
2.2.1 维纳滤波器
维纳滤波器是线性滤波器的一种。它基于最小均方误差准则,即要求滤波器的输出与期望输出之间的均方误差为最小。它也是一个最佳滤波系统。维纳滤波器可以有效的恢复被平稳噪声干扰的信号。
举例来说,对于观测信号f0(t):
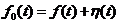 (2.1)
(2.1)
其中f(t)是我们期望恢复的信号,η(t)是噪声。这是一个典型的病态求逆问题,可以通过吉洪诺夫正则化来解决:
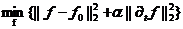 (2.2)
(2.2)
从(2.2)式可得到欧拉-拉格朗日方程,将其在频域进行处理,可以得到如下的频域关系:
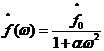 (2.3)
(2.3)
其中,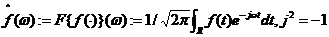 ,表示信号f(t)的傅里叶变换。显然,恢复的信号f是输入信号f0(t)在ω=0附近的一个低通窄带选择。事实上,这个解决方案对应于包含维纳滤波器的卷积,而α代表了白噪声的方差[13]。
,表示信号f(t)的傅里叶变换。显然,恢复的信号f是输入信号f0(t)在ω=0附近的一个低通窄带选择。事实上,这个解决方案对应于包含维纳滤波器的卷积,而α代表了白噪声的方差[13]。
2.2.2 希尔伯特变换
一个实值函数的希尔伯特变换可以简单的定义为原信号f(t)与1/πt的卷积结果。希尔伯特变换的重要用途便是从实值函数中构造出解析信号,从而将一维信号转变到二维复平面研究,使信号的幅度和相位有了更具体的表征[14]。
2.2.3 混频原理
混频是将两个信号非线性地组合在一起,从而在输出中引入交叉频率项的过程。最简单的混频器是乘法器。将两个真实信号与频率ω1和ω2相乘,分别在输出中创建混合频率ω1-ω2,ω1 ω2,这很容易用以下三角恒等式表示:
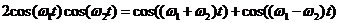 (2.4)
(2.4)
混合这两个独立解析信号:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: