摘 要

智能设备内嵌的加速度传感器，不仅能够通过感知加速度方向的变化来识别设备运动方式的改变，而且可以在语音信号作为激励时输出一个非线性的信号。本文首先利用FNN和Cao方法对加速度传感器输出的非线性信号进行了最小嵌入维数的求解。并根据两种方法在求解出的嵌入维数时的不同，比较了两算法的优劣性。又在此基础上，对李亚普诺夫指数（Lyapunov）进行了计算，验证了输出信号所具有的混沌特性。

本文又选用MFCC梅尔系数作为特征值，提取了加速度传感器输出的不同信号之间的梅尔系数并比较了不同信号之间MFCC梅尔系数之间的欧式距离。因不同信号梅尔系数之间距离差值较大，于是又以梅尔系数为特征值，利用支持向量机（Support Vector Machine，SVM）对此信号进行识别。这种方法在双人语音识别方面取得了较好的准确率。

关键词：Cao方法；FNN；相空间重构；Lyapunov；MFCC特征值；SVM

Abstract

The acceleration sensor embedded in the smart device can not only recognize the change of the motion mode of the device by sensing the change of the acceleration direction, but also output a nonlinear signal when the voice signal is used as an excitation. In this paper, the FNN and Cao methods are used to solve the minimum embedded dimension of the nonlinear signal output by the acceleration sensor. According to the difference between the two methods in solving the embedded dimension, the advantages and disadvantages of the two algorithms are compared. On this basis, the Lyapunov index is calculated to verify the chaotic characteristics of the output signal.

In this paper, the MFCC Mel coefficient is selected as the eigenvalue, and the Mel coefficient between different signals output by the acceleration sensor is extracted and the Euclidean distance between the MFCC Mel coefficients between different signals is compared. Because the difference between the different coefficients of the Mel coefficients is large, the Mel coefficient is used as the characteristic value, and the signal is identified by Support Vector Machine (SVM). This method has achieved good accuracy in double speech recognition.

Key words: Cao method; FNN; phase space reconstruction; Lyapunov; MFCC eigenvalue; SVM

目录

摘要 I

Abstract II

1.绪论 1

1.1研究意义和研究目的 1

1.2国内外研究现状 2

1.3论文实现流程及章节安排 2

2.加速度传感器输出信号的非线性研究 3

2.1 加速度传感器内部结构 3

2.2 相空间重构 3

2.2.1 FNN 3

2.2.2 Cao方法 4

2.3李亚普诺夫（Lyapunov）指数 5

3.梅尔系数 7

3.1声谱图 7

3.2同态信号处理 8

3.3 Mel频率分析 8

3.4 MFCC特征值提取流程 9

4.SVM双人语音识别 11

4.1原理 11

4.2函数间隔与几何间隔 11

4.3间隔最大化 13

4.4学习的对偶算法 14

4.5 线性支持向量机学习算法 15

5.实验结果展示 16

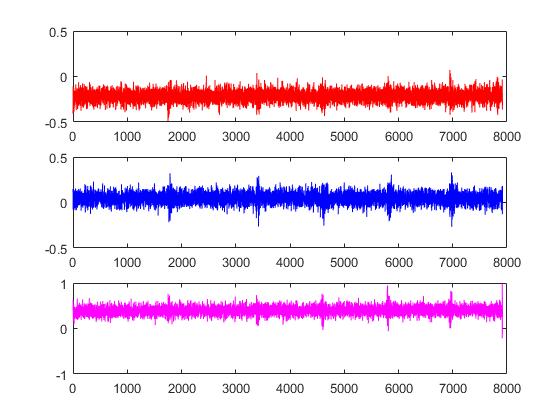
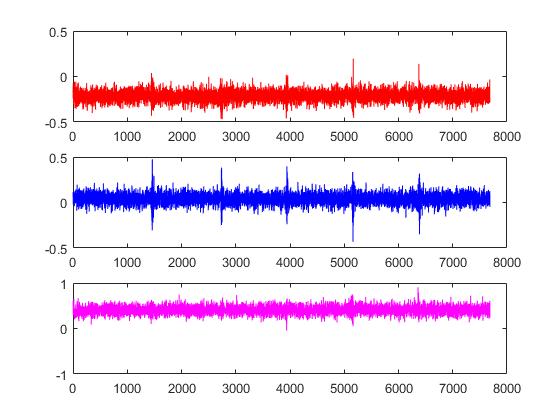
5.1 加速度传感器的输出信号 16

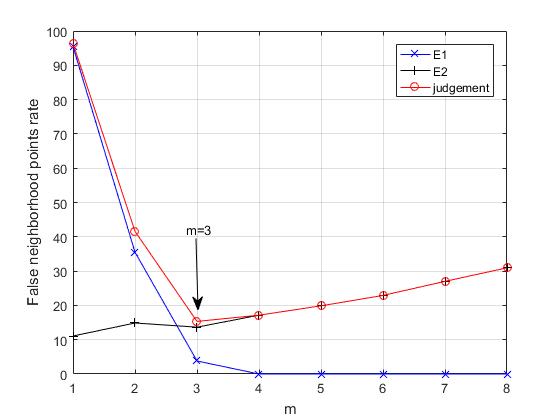
5.2 FNN求解嵌入维数 17

5.3 Cao方法求解嵌入维数 18

5.4 Lypunov指数的计算 19

5.5 Mel系数的提取及距离的比较 20

5.6 SVM对传感器输出信号的分类 21

5.6.1 设计思路 21

5.6.2 SVM分类结果 22

总结 24

致谢 25

参考文献： 26

1.绪论

1.1研究意义和研究目的

随着现代科技的发展，智能设备蓬勃兴起。作为智能设备“感知”外界的手段，嵌入在智能设备内部的智能传感器发挥着重要的作用。

相比于传统的电子设备，智能设备已经在我们生活个各个方面发挥着强大的功能，为我们的生活提供便利。例如智能手机和智能手表所具备的传统手机和手表所没有的附加属性。这其中的原因很大取决于移动芯片的强大性能和整合性，这在很大程度上增强了智能设备的实时运算能力，而嵌入在设备中的多种微型传感器则在扩展了智能设备的功能范围的同时，也为用户提供了良好的交互体验。

为了提高交互性能，手机等智能设备中会内嵌传感器。这些传感器从本质上来说是一种通过探测外界的光、热量、温度、信号等环境参数的物理装置。例如，本文所重点研究的加速度传感器，它能够探测到设备在其三个坐标轴上瞬时加速度变化值。人们最开始正是利用这些瞬时加速度的变化值来计算出运动速率和运动的方向，从而实现对携带智能设备的人体目标诸如走路、跑步等运动状态模式的识别。而又有研究者发现，对于一些满足特定条件的激励信号，一些内嵌的传感器也会产生响应。本文所研究的是在语音信号作为激励条件下，加速度传感器的非线性响应^[1]。

对于不同的场景，加速度传感器这种对语音信号产生响应的特性有多种意义。例如，在今天，利用语音来控制智能设备已经成为了一个新的人机交互方式。比如iOS中的Siri以及Android中的GoogleNow 作为语音交互平台，已经取得了很大的成功^[2]。但是在语音交互功能实现的过程中，为了能够实现随时对用户特定语音的唤醒的功能，作为采集语音信号的麦克风要保持工作的状态。这对智能手机中电量的消耗不可忽视，并且随着智能设备向着便携化的发展，人们对智能设备的体积大小不断有着新的要求，而质量优良的麦克风的体积时不可忽略的。如果利用类似加速度传感器的传感器来采集特定的语音，无疑对解决上述问题提供了新的方法。

在语音信号作为激励时，受到传感器硬件结构的限制^[3]，其输出的信号会体现出比较强的非线性特征，因此，本文首先以混沌理论为基础，从非线性动力学角度出发，以混沌理论为基础，通过信号相空间重构的方法揭示语音信号通过智能设备内置运动传感器后响应信号的混沌特征。在这之后，本文又通过梅尔系数（MFCC）作为特征值，利用SVM对传感器输出的信号进行分类，对加速度传感器输出的信号实现了较为准确的预测。

1.2国内外研究现状

本文首先对加速度传感器输出的信号求解了最小嵌入维数并进行了相空间重构。在相空间重构的问题上，自从塔肯斯（Takens）提出计算嵌入相空间维数大小是相空间技术的一个基本命题后^[4]，研究者便将其运用于各个领域。总的来说，这是一种可以将一维的系统非线性响应扩展到多维进行的方法。例如，同济大学的易攀科硕士，通过利用相空间重构技术来寻找心磁和心电信号的混沌特性，计算了吸引子的关联维和最大Lyapunov指数，最终重构了这两种信号的吸引子。这无疑对心类疾病的发现与诊断有着重要意义^[5]。又比如，暨南大学的聂振华博士通过相空间重构技术为结构损伤检测和健康监测，这对长期使用中的现代工程结构的安全检测有重要意义^[6]。

本文对加速度传感器输出的信号通过求解最小嵌入维数并计算lyapunov指数来进行相空间重构。并且又在此基础上又对加速度传感其输出的信号提取了特征值参数，实现了双人语音识别。

在语音识别的过程中，特征值的选定对训练和识别的环节有着重用的影响。感性预测系数（PLP）和线性预测系数（LPCC）以及梅尔导频系数（MFCC）是现在常用的特征值。由于MFCC抗噪能力强且对环境的依赖程度低^[7]。因此本文选用MFCC为特征值来进行语音识别。

1.3论文实现流程及章节安排

本文所用实验的数据来源于语音信号作为激励，选用智能手机内嵌加速度传感器作为系统得到所输出的非线性信号。在本文的第二部分，将介绍加速度传感器的内部结构并介绍相空间重构中的一些重要指标的求解方法。本还还比较了求解相空间重构参数时不同算法的优劣性。其次，在文章的第三和第四部分，本文分别介绍了MFCC参数和支持向量机（support vector machine, SVM）这一分类器。利用MFCC梅尔系数作为特征值，利用SVM这一分类模型进行分类是本文实现双人语音识别的主要手段。文章的第五部分为实验结果展示部分，论文总体的框图如图1.1所示。

图1.1 论文结构框图

2.加速度传感器输出信号的非线性研究

2.1 加速度传感器内部结构

如今大多数智能设备内置的加速度传感器主要由三个部分组成——弹簧腿（spring legs）、惯性质量(inertial mass)和固定指状物(stationary fingers)。当语音信号作为激励时，此时加速度传感器内部的惯性质量将会振动，从而导致固定指状物之间电容的变化，加速度传感器就会产生相对应的响应^[1]。因为智能设备内嵌的传感器的主要任务并不是采集语音信号，因此受到硬件的限制，输出的信号将产生非线性的变化。该响应信号是离散信号，可以表示为：

(2.1)

其中n为离散采样的点的序号，τ和m分别为时间间隔和嵌入维数。时间间隔τ可以根据大量实验来估计，嵌入维数m求解的主要途径为FNN（False nearest neighbors）和Cao方法。在文章的2.2.1和2.2.2小节，这两种方法将本介绍。求解的结果和优劣性的比较将在5.2和5.3小节展示和分析。

2.2 相空间重构

当语音信号作为激励时，智能设备内嵌的加速度传感器将输出一个非线性信号。相空间重构法自提出以来，在构建非线性信号模型的过程中就起到了很大的作用。总体来说，决定相空间重构质量好坏的参数为时间间隔τ和最小嵌入维数m。时间间隔τ可以通过大量的实验来测的，而最小嵌入维数求解的方法有很多。常用的方法时FNN假邻域法和Cao方法。在下面的章节中，本文将介绍这两种方法的基本原理并比较两者的优劣性。

2.2.1 FNN

FNN（False nearest neighbors），又称伪邻域法，是一种获得相空间重构最佳嵌入维数的一种常用方法。改方法基于一种假设：在一个合理嵌入维数m的条件下，两个彼此相邻的点会继续保持相邻，即使嵌入维数增加。

伪邻域法（FNN）的主要思想是检查沿着信号轨迹的点的邻近点的数量是否随着嵌入维度的增加而变化。 即，在嵌入维度太低的情况下，许多邻近点将是假的，但是在适当的嵌入维度或更高的维度中，邻近点则是真实的。 因此随着维度的增加，假临近点将不再是临近。 因此，通过检查邻居的数量如何随维度而变化，可以确定适当的嵌入^[8]。

因此，伪邻域法（FNN）通过判断某个嵌入维度下的假邻居点数是否为零来计算最小嵌入维数。根据所选择的时间延迟τ，在m维空间中，每个相位点矢量可以显示为：

(2.2)

使用表示的第i个临近点，则它们之间的距离定义为：

(2.3)

如果时间序列被提升到m 1维，则原始两点之间的距离将变为：

(2.4)

将相对差值阈值设置为。如果在将维度从m增加到m 1时距离之间的差异大于此阈值，则这些点将被判断为假邻居点。这可以显示为：

(2.5)

由于本文中使用的实验数据不可避免的混有一定的白噪声，但是对于白噪声，利用上述公式确定的嵌入维数m往往很小。但是事实上，有学者已经证明白噪声的嵌入维数应该为无穷大。其原因是，对于上述讨论的和点，如果是在白噪声时间序列中，即使他们是最邻近点，它们之间的距离也可能会很大^[9]。因此，在有白噪声影响的序列中，还需要添加另一个阈值来判断错误的邻居点：

(2.6)

在上述等式中：

(2.7)

(2.8)

如果建立了不等式，则可以判断为假邻居点。

2.2.2 Cao方法

FNN算法在求解嵌入维数时引入了两个阈值，这带有一定的主观性。如果选择不同的阈值，求出的嵌入维数会不同。Cao为了解决两个阈值方面的FNN选择问题，改进了FNN算法，其具体步骤与FNN类似。在FNN算法中，不等式（2.5）是关于时间n的统计量，并且每次使用相同的阈值来判断它是否是假邻居显然是不合理的^[9]。Cao把（2.5）式转换为：

(2.9)

其中和 为m维空间的第i个向量以及与这个向量距离最近的点，即最临近点。

Cao又定义了：

(2.10)

(2.11)

E(m)表示当嵌入维度为m时，时间序列的每个点与其邻居点之间的距离的统计值。而E *（m）表示当嵌入尺寸从m变化到m 1时距离增加的统计平均值^[10]。之后计算：

(2.12)

(2.13)

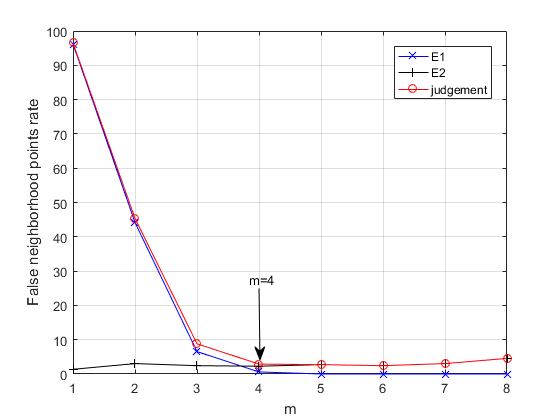
如果在m大于某个值之后E1（m）没有改变，则该序列是确定的序列。

此外，若时间序列是随机序列，即并且序列是不可预测的，则E2（m）的值始终为1。 而对于确定性序列，总有一些m值不能使E2总是等于1。

2.3李亚普诺夫（Lyapunov）指数

验证动力学特征的指标有很多，李亚普诺夫指数（Lyapunov）无疑是其中十分重要且常用的指标。这是因为通过分析李亚普诺夫指数的值，我们可以直观的得到系统是否存在动力学的混沌特性。

其具体的方法为：当李亚普诺夫指数大于零时，系统具有动力学混沌特性；而当李亚普诺夫指数小于零时，系统并不存在动力学混沌^[11]。

其背后的原理可概括为：李亚普诺夫指数实际上代表了相空间中相邻的轨道间收敛或发散的平均指数率。因此如果李亚普诺夫（Lyapunov）指数大于零，那么在相空间中，无论初始的两条轨线的间距有多么小，当时间变化时，轨线之间的间距都会以指数率的速度增加，直至无法预测的结果，这就是混沌现象。

计算李亚普诺夫指数的方法为，如果相空间重构的嵌入维数为m，时间延迟为τ，并且设时间序列为,则重构的相空间可以表示为：

(2.14)

选取作为初始点，设与该点最近的点为,计算这两点的距离。随着时间的变化，不断追踪这两点之间的距离。假设当时间为时，这两点的距离大于某规定值，保留此时的,重复上述的过程，知道达到时间序列的重点，总的迭代次数为M，则最大李亚普诺夫指数为^[12]：

(2.15)

3.梅尔系数

基于人的听觉机理，Davis和Mermelstein在1980提出一种基于人耳听觉特性的特征值参数，叫做Mel频率倒谱系数（Mel Frequency Cepstrum Coefficient, MFCC）。

与普通实际频率倒频分析不同,据史蒂文斯和沃克曼说,在1940年工作中,他们得到的结论是人类的感知频率与实际频率之间的关系满足下式^[13]:

(3.1)

这里，实际频率f的单位是Hz。当f为1000Hz以下时，和f的关系可以表示为线性关系；当f在1000Hz以上，则两者的关系表现为对数的增长。

为了将实际频域转换为Mel频率，需要设计一组滤波器，即Mel滤波器。经过Mel滤波器转换出来的Mel频率倒频系数的分析更加着眼于人耳的听觉特性。因此，在语音识别领域可以充当很好的特征值参数^[13]。

梅尔系数（MFCC）是在语音识别中经常使用的特征值。因为加速度传感器输出的非线性信号是语音信号作为激励的，所以该输出信号也具备一些语音信号的特点。因此，本文讲传感器的输出信号的梅尔系数作为特征值，对该输出信号进行识别。具体的结果将在第5节展示。

3.1声谱图

如果将语音信号进行短时傅里叶变化的处理，我们就可以研究语音信号的短时频谱与时间之间的关系。本文研究的信号是在语音信号激励下，通过加速度传感器输出的信号，具有和语音信号相似的性质，因此也可尝试对该信号用语音信号处理的方法来进行处理。

人们最初对语音信号的短时频谱的研究，是通过频谱仪进行的。将通过频谱仪的语音信号的强弱用记录在纸上的灰度表示：输出的信号强，则记录的灰度身；反之，则灰度浅。具体的操作流程为，首先将分为很多帧的语音的每一帧进行短时FFT计算，获得的频谱表示频率与能量的关系。

然后，将一帧语音的频谱通过坐标表示。频谱图的振幅映射到灰度级。映射的准则为：幅度值越大，灰度级越大（黑）；幅度之小，灰度级越小（白）。

这样做的优点为可以增加时间参量，这样可以同时显示一段语音的频谱，不但可以通过观察每一帧的灰度级大小得到信号动态变化的信息，而且可以通过观察共振峰和它们的转变来更好的识别声音^[14]。

3.2同态信号处理

日常生活中的许多信号，例如语音信号和图像信号，它们并不是加性信号而是乘积性信号或者卷积性信号。如果要对进行研究，就需要用到同态信号处理，又称倒谱分析法，它可以将非线性问题转换为线性问题^[15]。

语音信号的频谱图的主要峰值叫做共振峰，它们携带着这一语音信号的主要频率部分。共振峰携带着语音信号的辨识属性，因此其在语音识别方面有着很重要的作用^[14]。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：