摘 要

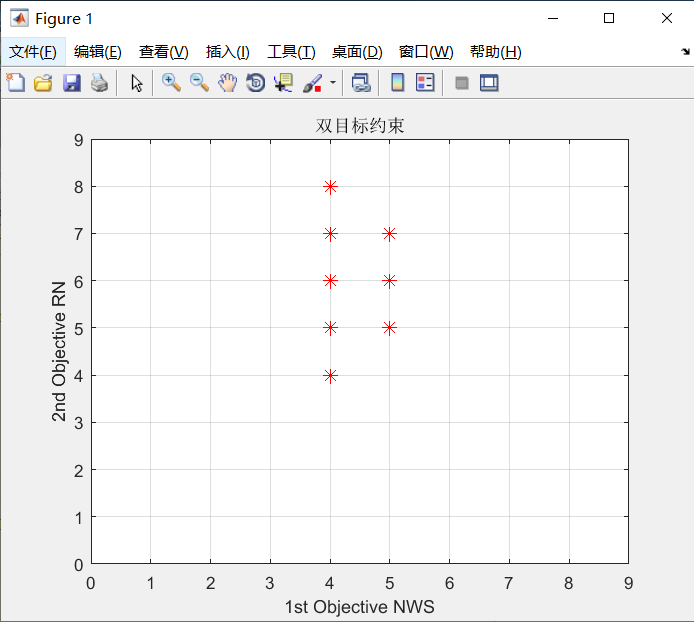
当今世界，资源匮乏和环境变差是人类面临的两大问题，废弃产品对环境的污染也是相当巨大的。对废弃电子产品的回收可以实现对某些资源的重复利用，也可以通过清除有害部件减小其对环境污染。本文研究的是资源约束条件下的拆卸线平衡问题，不同于简单的拆卸，本文考虑到了进行拆卸操作时某些资源（诸如工人，机器人，能源等等）可能会有限，因此就产生了资源约束拆卸线平衡问题。通过自己定义拆卸任务及其任务时间，任务需要资源类型等，建立多目标数学模型，然后通过LINGO优化软件进行模型验证，最后通过NSGA-III算法解决该问题，在MATLAB上进行仿真。

关键词：资源约束 拆卸线平衡 NSGA-III MATLAB

Abstract

In today's world, the lack of resources and environmental change is the two major problems facing mankind, waste products on the environment pollution is also quite huge. Recycling of waste electronic products can achieve the reuse of certain resources, or it can reduce its environmental pollution by removing harmful components. This paper studies the problem of disassembly line balance under the condition of resource constraint, which is different from simple disassembly, this paper takes into account that some resources (such as workers, robots, energy, etc.) may be limited during disassembly operation, so the balance problem of resource constraint disassembly line is created. By defining the disassembly task and its task time, the task needs the resource type and so on, the multi-objective mathematical model is established, then the model is verified by LINGO optimization software, and finally the problem is solved by NSGA-III algorithm, and the simulation is carried out in MATLAB.

Keyword: resource constraint disassembly line balance NSGA-III MATLAB

目录

第1章 绪论 1

1.1研究目的及意义 1

1.2拆卸先平衡问题研究现状 1

1.3研究目标及本文结构 2

第2章 资源约束拆卸线平衡问题的概念和数学模型 4

2.1资源约束拆卸线平衡的相关概念 4

2.2资源约束拆卸线平衡问题的数学模型 4

2.2.1 模型假设 5

2.2.2 符号说明 5

2.2.3 任务说明 6

2.2.4 数学模型 7

2.3小结 8

第3章 LINGO验证数学模型 10

3.1 LINGO简介 10

3.2用LINGO对数学模型求解 10

3.3结果分析 13

3.4小结 13

第4章 NSGA-III算法实现 15

4.1 NSGA-III算法简介 15

4.2 NSGA3算法的基本流程及关键步骤 15

4.2.1 NSGA3算法基本流程 15

4.2.2 NSGA3算法关键步骤 16

4.3 NSGA3算法流程图 16

4.3种群初始化 18

4.4编码与解码 18

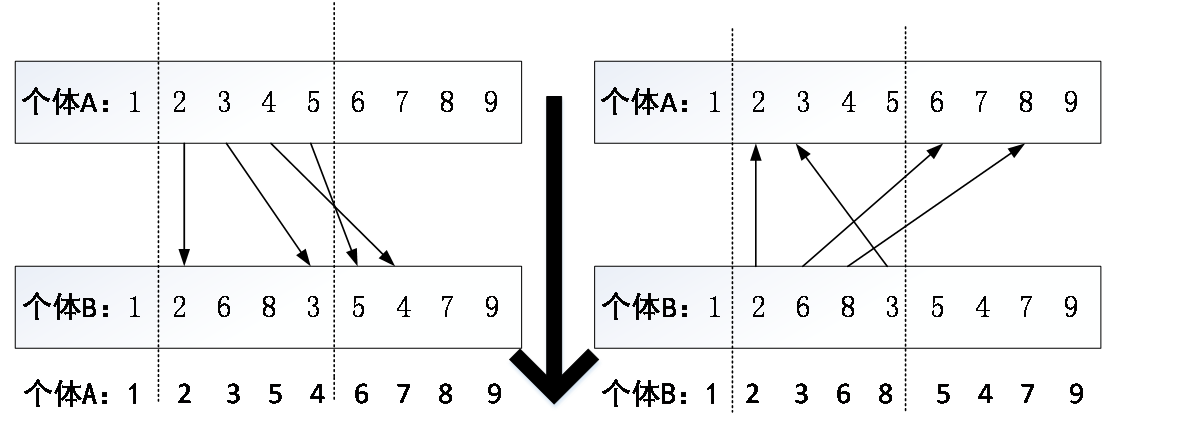
4.5 选择交叉变异 19

4.5.1模拟两点交叉 19

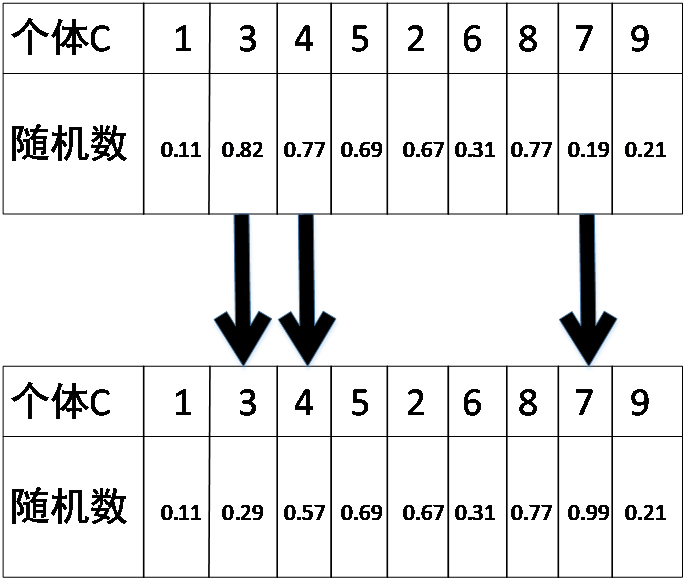
4.5.2多项式变异 20

4.6 NSGA3算法实现 21

4.7小结 26

第5章 总结与展望 27

5.1总结 27

5.2展望 27

致谢 29

参考文献 30

附录 31

第1章 绪论

1.1研究目的及意义

进入21世纪，全球的工业制造业得到了极大的发展，人类的物质文明空前发达。在人类享受这些工业品电子产品带来的便利的同时，也产生了各种各样的废弃产品，加之电子产品的寿命一般较短，报废产品数量也日益增多。据不完全统计，全球每年产生的报废电子产品有2500万吨到5000万吨^[1]。我国人口基数大，每年产生的报废产品数量更是不少。诸如电脑，汽车，手机，冰箱等等废弃产品，如果不及时加以处理，任由其堆积如山，则会对环境产生不可逆转的损害。反之，如果对其加以回收，取其有用部件，则可以实现对资源的循环利用，也可以大幅度减少对环境的损害。再者，地球上的资源并不是取之不尽，用之不竭的，都是用一点少一点，因此对报废产品的回收利用在对于资源的节约上就显得尤为重要了。综上所述，对报废电子产品进行回收不仅仅能大幅度减少对环境的污染，也能很大程度上的节约资源，随着国家对报废产品回收的重视，加之进行废弃产品的回收也有相当可观的利益，废弃产品回收逐渐朝着规范化、产业化的方向发展，对于废弃机电产品的回收，国家也开始通过立法的方式来规范管理，也是响应党的保护环境，节约资源，可持续发张，建立美丽中国的号召。

对废弃产品回收的主要目的是从废弃产品中通过获得可用有益的零部件或材料，通过清洗加工等步骤达到重新投入新产品的使用中，从而达到节约资源的目的。除了回收有用资源外，还要对有害零部件进行处理，防止其对环境造成污染破坏。对废弃产品的回收的主要就是拆卸产品，通过这个阶段，可以将有用可回收零部件与无用以及有害部件进行分离，从而实现对有用零件的回收利用以及对有害部分的处理。这个阶段则是在拆卸线中进行的。作为制造回收业，为了利润最大化，当然要在对废弃产品进行拆卸回收时考虑资源能耗问题。为了要使利益最大化，相对的在对一个废弃产品进行拆卸时就要使工人数量，机器人数量，工作站数，消耗的能源等尽可能的小，因此就有了资源约束下的拆卸线平衡问题，在现实生产中，考虑资源约束是很有必要的。

1.2拆卸先平衡问题研究现状

拆卸线已存在一个多世纪，但是对拆卸线平衡问题（Disassembly line balancing problem,DLBP）的研究于2001 年才被 Gupta,Gunger 等人首先提出，分析了拆卸线平衡问题中的复杂性和其不确定性，同时也指出了拆卸线和装配线的相同处和不同处^{[2 3]}，2002年，Gupta提出了DLBP是一种组合优化问题，并于2006年证明了DLBP是NP-hard问题。

近年来, 拆卸线平衡问题也引起了国内外研究学者们的广泛关注, 并取得了大量研究进展。对DLBP的研究主要是从模型和求解算法两个方向开展研究。模型方面，有Altekin等 在2008; Kocet等在2009;Altekin 和 Akkan在2012年研究的顺序相依型，Avikal 和Mishra,在2012， Avikal 等于2013 提出的U型，Aydemir和Turkber于2013年于2015年提的平行型，还有Agrawal和Tiwari于2008年提出的混合模型。求解算法，有Koc等在2009年，Bentaha等在2015年提的精密解决算法，McGovern和Gupta在2007年提出的遗传算法，Kalayci和Gupta在2014年提出的禁忌搜素算法^[3]。这些问题的相同点是在最有效率的情况下都用了操作人员和机器。但是，由于拆卸线的一些性质如：危险性，有爆炸材料和紧密工具，所以需要特殊的资源。由于这些情况需要使用特殊的装备和专业的工作人员，因此有必要形成一个产业。为了从拆卸线中获得最大效益，这些装备和工人以最高效率添加到产线中，例如最大利用率和最小工作站数。尽管Pinnoi和Wilhelm于1997年，Agpak和Gokcen于2005年，Mete和Agpak于2013年都提出了资源约束下的拆卸线平衡问题，但是这个问题还没有得到完全解决。将DLBP的求解方法总结整理成图^[4]，如图1.1所示：

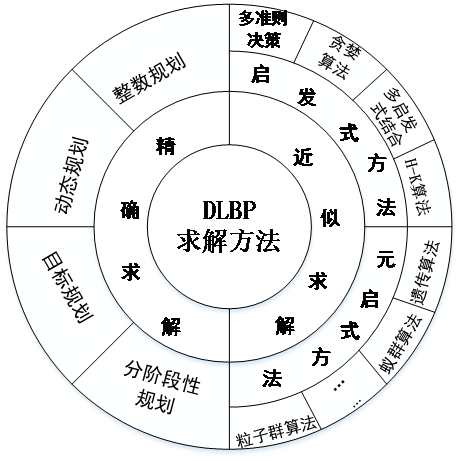
图1.1 DLBP求解方法图

1.3研究目标及本文结构

本文的研究目标是在进行拆卸线平衡处理时，在流水线节拍固定的条件下，最小化工作站数，最小化使用资源数。通过对资源约束拆卸线平衡问题进行多目标数学建模及算法仿真，得到最优化目标。

本文的结构：第一部分时对研究课题背景的介绍以及国内外研究现状的综述；第二部分将对资源约束拆卸线平衡问题进行多目标建模，并通过LINGO等软件验证数学模型的正确性；第三部分则是在给定的条件下的实例进行仿真，对得到的结果进行分析比较说明；第四部分进行总结及展望。

第2章 资源约束拆卸线平衡问题的概念和数学模型

2.1资源约束拆卸线平衡的相关概念

拆卸线平衡问题（Disassembly Line Balancing Problem,简称DLBP）是于2001年才被Gupta等人提出的新概念。拆卸之前被认为是装配的逆过程，直到1994年Brennan等指出拆卸线不仅仅是简单的装配线的逆过程，到了2001年，Gupta和Gungor等指出了拆卸线和装配线的相同点和不同点。

拆卸可以在单个拆卸单元和拆卸线上进行。拆卸单元适合于小型产品的拆卸，使用起来比较灵活，但是具有拆卸效率不高的缺点。拆卸线适合于中型和大型的产品拆卸，能对大规模任务进行拆卸操作，同时也能大大的提高拆卸效率^[4]。

拆卸又分为完全拆卸和不完全拆卸。完全拆卸是指经过拆卸后不能的零部件不能在拆卸；不完全拆卸在拆卸后的零部件还可以继续拆分为更小的零部件不完全拆卸常常在修理升级产品时使用，不完全拆卸又被称为选择性拆卸。

拆卸作业时间指完成一项拆卸任务所需要的标准时间。

循环时间（Cycle Time）指的是，在一条拆卸线中，每个工作站都有自己的工作时间，超过了这个工作间后，工作站就会停止工作，这个工作时间就称为循环时间。分配给每个工作站的任务执行总时间应该小于此工作站的循环时间。

闲置时间（Idle Time）^[5]：表示的是一个工作站的循环时间减去处理任务所用时间剩下的时间。通常来说，需要多个工作站进行拆卸任务时，应该使各个工作站的闲置时间保持相对平衡。

拆卸线平衡（Disassembly Line Balancing Problem,简称DLBP）^[6]的定义是基于生产工作过程，根据拆卸产品作业需求，按照一定的节拍时间分配拆卸工作站和作业人数，获得良好的拆卸线平衡指标如最小化工作站数、最小化工作站空闲时间等）的活动。

资源约束拆卸线平衡问题（Resource Constrained Disassembly Line Balancing Problem,简称RCDLBP）^[7]是指，在实际生产中，当工人或机器人在拆卸流水线上执行拆卸任务时，有时会需要特定的资源，如机器人、特定设备、材料、工具、技能良好的人员等，这些特定的资源是有限的，换言之，每个工作站能同时拥有或使用的数量有限，也就是资源有限（即约束），这就衍生了资源约束的线平衡问题。

2.2资源约束拆卸线平衡问题的数学模型

本文考虑了带资源约束条件的DLB问题。此课题的目标是找到一个能够解决有资源约束的DLB问题的解决方案。在此目标下构建数学模型。本文所建立的假设数学模型集合了Agpak和Gokcen于2005年提出的简单的资源约束装配线平衡问题以及Koc等于2009年提出的DLB整数规划公式^[8]。具体到本文的目的是建立一个能最小化工作站数以及最小化分配给工作站的资源数目。这些资源是工作站在进行拆卸时必需的，往往有机器人，工人，能源或者是特殊的机器等。本文只考虑一种资源—-机器人，约束的是分配给工作站的机器人总数目。机器人有两种，一个R1类型，一个R2类型。一个任务只需用到一种类型的机器人即可完成操作。例如，机器人R1可以用执行任务{1，3，5，7，9}，机器人R2可以用来执行任务{2，4，6，8}。因此各个任务的交集是空集群（Agpak和Gokcen，2005）^[3]。RCDLB问题的相关数学模型和符号说明如下：

2.2.1 模型假设

在本文中，资源约束拆卸线平衡问题需在以下假设条件下进行：

1.每个任务所需要的拆卸时间已经知道；

2.每次拆卸能够提取其中一个或多个部分，即不会对不能在拆卸的任务执行操作；

3.每个任务仅仅被分配到一个工作站上；

4.分配给每个工作站的任务的总处理时间必须小于或等于循环时间；

5.任务之间的拆卸优先关系必须满足；

6.各个任务之间没有相互干扰。

2.2.2 符号说明

本小节对该问题要建立的数学模型中用到的一些符号进行说明解释，如下所示：

i：任务序号, i∈[1,I];

j：工作站序号，j∈[1,J];

r：机器人类型，r∈[1,R];

CT：循环时间；

NWS：工作站数量；

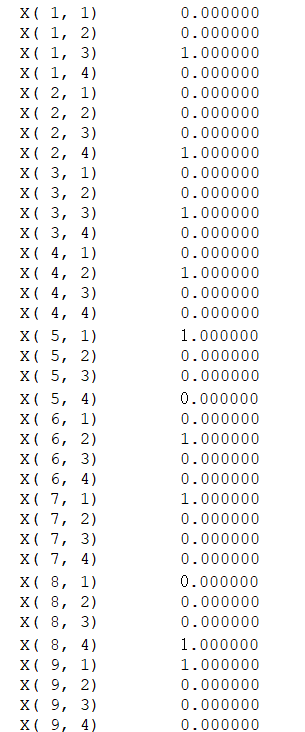
：值为1表示工作站j开启，为0表示不开启；

：值为1表示任务i分配给工作站j，0表示其他；

：表示第i个任务的拆卸时间；

：值为1表示工作站j有机器人r,0表示没有机器人r。

2.2.3 任务说明

本小节给出一个自己假定的拆卸产品，总共9个任务的拆卸任务关系示意图，如图2.1示：

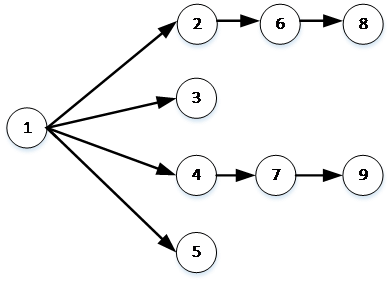
图2.1 任务拆卸优先关系示意图

图中，各个数字即表示各个拆卸任务，有箭头连接的两个任务，表示两者之间有优先约束关系，箭头起始端的任务必须在终端的任务之前完成。根据拆卸任务的优先关系图可以得出产品拆卸的零件优先关系矩阵^[9]，矩阵如下：

1 2 3 4 5 6 7 8 9

1 0 1 1 1 1 0 0 0 0

2 0 0 0 0 0 1 0 0 0

3 0 0 0 0 0 0 0 0 0

4 0 0 0 0 0 0 1 0 0

5 0 0 0 0 0 0 0 0 0

6 0 0 0 0 0 0 0 1 0

7 0 0 0 0 0 0 0 0 1

8 0 0 0 0 0 0 0 0 0

9 0 0 0 0 0 0 0 0 0

该矩阵中，若两个零件A和B存在拆卸的优先关系，如果A必须在B之前拆卸，A对应行，B对应列，则P（A，B）=1;否则P（A，B）=0；例如P（1，2）=1，P（1，3）=1；P（1，1）=0，P（2，1）=0，P（1，6）=0；

下面对各个任务的拆卸时间以及所需要的资源（机器人）类型进行假设说明，设每个工作站的节拍时间CT=25s，具体任务说明如表2.1所示：

表2.1 任务执行时间及所需资源类型表

2.2.4 数学模型

本文要达到的目的是最小化工作站数和最小使用资源（机器人数量）。最小化工作站为第一目标，最小化资源数目为第二部目标。每个拆卸任务都需要通过一种机器人来完成，本文假设机器人的类型一共有两种，且所有的拆卸任务都能通过这两种机器人（R1或R2）完成拆卸，详见表2.1，且假设每个工作站只需装配的某类机器人可以一直使用，不考虑损坏等情况。

根据问题假设说明建立目标函数^[10]为：

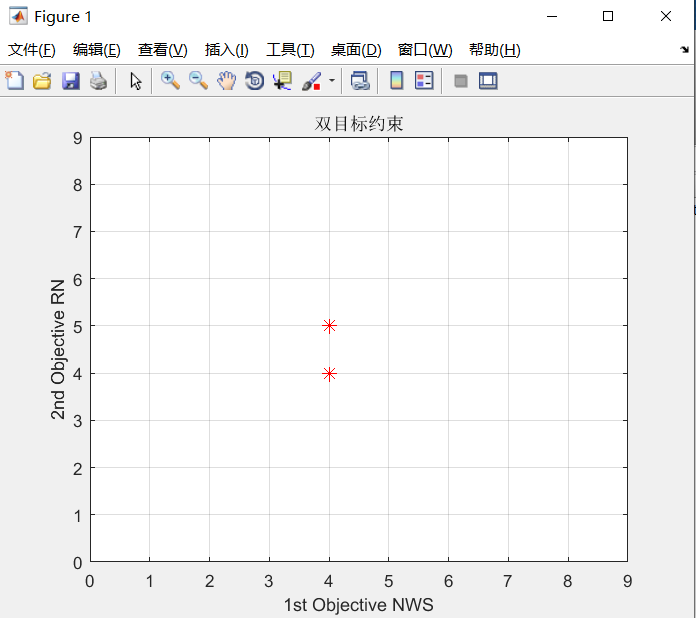
Min F=[NWS,RN]

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：