基于数字图像处理的织物缺陷检测研究毕业论文
2020-02-23 21:53:33
摘 要
本文采用Gabor滤波器来检测常见织物图像中的疵点,目的是分离图像中的缺陷区域,从而实现纺织品缺陷检测的自动化。本研究基于机器视觉在工业检测中的应用,大大提高了生产过程中的检测效率,具有一定的应用价值。
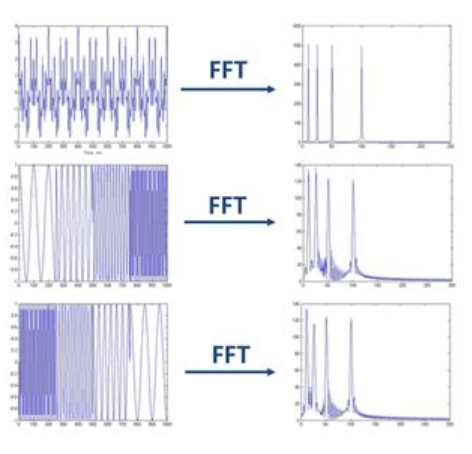
当研究信号的频率特性时,傅里叶变换一直是我们常用的工具,但是傅里叶变换对于频域局部特性的表现能力较差,在纹理图像的解析过程中并没有很好的表现。而Gabor滤波器是一种有效检测织物疵点的工具,完善了傅里叶变换的不足,并且通过对于Gabor滤波器参数的研究,我们可以在时间域和频率域均保持良好的识别精度。
在对织物的图案进行初步研究后,我们可以发现,纺织物图像一般含有一定的纹理特征,而其中的疵点往往聚集在某一区域。对应到频率域,纹理部分对应的是高频部分,而相对集中的疵点则对应的是低频部分,在选取合适的Gabor滤波器参数后,我们可以将图像的纹理部分与缺陷部分分离开来,在经过阈值分割后,将疵点标记出来。
为综合各个方向的纹理特征,本文同时采用了多通道的Gabor滤波器,在此基础上进行图像融合,进一步提高了识别的准确率。
关键字:傅里叶变换;Gabor滤波器;图像融合;阈值分割
Abstract
In this paper, Gabor filter is used to detect the defects of fabric images. The purpose is to separate the defect area in the image, so as to realize the automatic realization of textile defect detection. This study is based on the application of machine vision in industrial inspection, which greatly improves the detection efficiency in the production process and has a certain application value.
When studying the frequency characteristics including the signal, the Fourier transform has always been our helpful tool, but the Fourier transform has poor performance in the local characteristics of the frequency domain, and does not perform well in the process of analyzing the texture image. The Gabor filter is a tool for effectively detecting fabric defects. The Gabor filter has better resolution in the spatial domain and frequency domain. By studying the Gabor filter parameters, we can maintain both the time domain and the frequency domain with good recognition accuracy.
After a preliminary study of the pattern of the fabric, we can find that the textile image generally contains certain texture features, and the defects are often concentrated in a certain area. Corresponding to the frequency domain, the texture part corresponds to the high-frequency part, and the relatively concentrated defect corresponds to the low-frequency part. After selecting the appropriate Gabor filter parameters, we can separate the texture part and the defect part of the image. After the threshold segmentation, the defects are marked.
In order to synthesize the texture features in all directions, a multi-channel Gabor filter is adopted in this paper. Based on this, image fusion is performed to further improve the recognition accuracy.
Key Words:Fourier Transform; Gabor filter; Image fusion; Threshold segmentation
目录
摘要 I
Abstract II
第1章 绪论 1
1.1 课题背景及意义 1
1.2 国内外研究现状 1
1.2.1 统计法 2
1.2.2 频域法 2
1.2.3 模型法 3
1.3 研究内容与预期目标 4
第2章 傅里叶变换 5
2.1 傅里叶变换原理 5
2.1.1 一维傅里叶变换 5
2.1.2 二维傅里叶变换 5
2.2 简单图像滤波 6
2.3 傅里叶变换的意义及不足 7
第3章 Gabor滤波器 9
3.1 一维Gabor滤波器 9
3.2 二维Gabor滤波器 10
3.3 波长λ参数影响 10
3.4 角度θ参数影响 12
3.5 标准差σ参数影响 13
第4章 检测系统设计 16
4.1 OpenCV简介 16
4.2 算法思路综述 16
4.3 获得滤波器参数 17
4.4 多角度滤波与图像融合 18
4.5 阈值分割 19
第5章 实验结果及分析 21
5.1 织物疵点描述 21
5.2 实验环境 21
5.3 实验结果展示 22
5.4 实验结果分析 25
第6章 结论 26
参考文献 27
致谢 29
第1章 绪论
1.1 课题背景及意义
纺织业是我国轻工业的支柱行业之一,在加入WTO组织后,纺织品是我国重要的商品贸易源。在带来巨大贸易契机的同时,纺织品质量控制也成了决定成败的重要关口。在相关的新闻报道中,由于部分织物的质量达不到国际标准,造成纺织业出口损失严重。因此,如何提高纺织物质量检测的效率与准确率,成了提高国计民生的重大课题。
纺织品在生产及进入市场过程中必须经过各种各样的测试及检查,其中织物的疵点检测是当中最为重要的部分。在自动化技术没有普及之前,这个检测的过程还是依靠人力来完成,带来的弊端也是显而易见的:(1)效率不高,人的工作能力及工作时间有限,对于成规模的检测环节需要大量的人力物力。(2)检验的标准与结果受到检测人员主观状态的影响,产生的误差较大。
基于上述原因,依托于近年来在信号处理及模式识别领域相关技术理论的突破,近十年来,织物的疵点检测,以及计算机视觉技术在工业检测领域的应用,成为了国内外学者研究和关注的热门方向。计算机数字图像处理技术很大程度上提高了织物疵点检测的准确性与效率。但同时也有相关研究指出,因为检测物体与缺陷目标在纺织领域均具有相当的复杂性,疵点检测是最难以实现自动化的[1],因此,这个方向仍有巨大的研究潜力。
其中Gabor滤波器因为在时域和频域的均衡表现,被广泛应用在了各种图像处理及模式识别场合,如Gabor滤波器结合LBP方法是一种流行的人脸检测算法[2]。在缺陷检测的场合中,Gabor滤波器同样有优良的表现,克服了傅里叶方法的不足,同时兼顾了在频域和时域的分辨能力[3]。并且可以通过滤波器参数的选择,达到我们想要的检测效果。
本文主要基于Gabor滤波器的理论,设计缺陷的自动化检测系统,并且在采集的织物疵点图像上进行试验,有助于实现自动化检测织物疵点,因此本文的研究有其必要性。
1.2 国内外研究现状
织物的缺陷检测,根据织物有无图案,可以粗略分为有图案的织物表面疵点检测和无图案的织物表面疵点检测。在本次研究中,以无图案织物表面疵点检测为主,选取的图像均是无图案的实验样本。对于国内外研究进展的叙述也局限在无图案织物检测的范围之内。
目前对于织物疵点检测的研究主要有三个方向,分别是统计法、频域法和模型法。我将分别介绍这三个方向的研究进展。
1.2.1 统计法
如果织物表面图案在小部分区域内是不规则的,而在整体上又表现出某种规律性,那么我们可以认为织物表面呈现了一定的纹理性。这样的纹理特征可以运用统计学方法提取,针对图像的灰度属性有较好地表示能力,将图像背景和疵点信息通过统计属性区分开来。常见的方法包括自相关函数、共生矩阵、分形维数与数学形态学等。
自相关函数可以用来描述图像中纹理厚度的变化,并且它通常用于估计织物垂直和水平方向重复单元的长度特性。Wang等人基于自相关函数理论来拟合织物纹理的重复单元,继而计算其大小,并据此来分割图像[4]。文献[5]计算经纬方向的自相关函数来构造基元模板,从而得到每个纹理基元与模板的差值,通过对于疵点区域的增强来实现图像分割。自相关函数对于纹理规律性较强的图像有较好的检测效果,但是如果缺少作为参照的基元模板,或者原始图案中的噪声较大使得纹理的规律性并不突出,那么检测的效果就会大打折扣。
灰度共生矩阵是一种图像的二阶统计特征。文献[6]用GLCM计算图像,提取二阶矩、相关性、对比度等特征向量,并以此作为支持向量机(SVM)的输入,利用机器学习方法完成织物疵点的检测。文献[7]提出的方法结合了灰度共生矩阵和统计直方图,得到了良好的检测结果。灰度共生矩阵在特征提取性能上优于自相关方法,但带来的问题是参与计算的矩阵维度过高,为解决维度爆炸的问题,也有学者提出类别共生矩阵来尝试解决这一问题[8]。
分形维数可以用来描述不规则图像的统计特性,如粗糙程度等。计算的方法是将图像看成是一个基于灰度的曲面,通过一定的统计方法计算得到该曲面的粗糙程度。文献[9]提取了四个分形特征,以此作为支持向量机的输入,从而克服了单一分形易忽略纹理局部信息的问题。文献[10]将二维数据沿纵横方向投影,利用一维分形提取特征,大大提高了分形的计算速度。
数学形态学的主要思路是利用一定形状的结构元素对图像进行变换,从而从图像中提取相应的特征。文献[11]在对图像进行预处理后,利用阈值分割将图像转换为二值图像,并对其进行形态学重建,最后的检测成功率高达92.8%。Celik等学者结合了线性滤波器与数学形态学,并利用神经网络进行识别,取得了一定的成功率[12]。
1.2.2 频域法
将信号变换到频域进行处理是我们在信号处理领域一种常见的思路,疵点图像的背景纹理部分和疵点部分在频域上的能量有所区分,图像可以转换到频域,然后可以处理图像的频域信息。
傅里叶变换是常见的信号从时域向频域转换的工具。Millan等研究者通过傅里叶变换提取图像特征,进而设计用于分离纹理与疵点的带通滤波器参数,仅仅通过设计不同尺度的滤波器就可以把需要的信息凸起出来[13]。傅里叶变换的劣势在于对于局部性并没有很好的支持,因此对缺陷的定位能力较差。
小波变换是另一种流行的时频分析方法,对于不同的要求,可以有效分析图像的纵横和对角信息,利用这一性质,可以用来进行疵点的检测。文献[14]将最大熵理论与小波变换相结合,求出在经过小波变换后的垂直子图与水平子图,并求出其最大熵与平均熵,完成目标检测。文献[15]重复使用小波变换,多重分析图像,分离图像经纬度纹理信息,经过改进后也可应用于经纬变形场景。在使用小波变换的过程中,小波基的选择对最终的检测结果有很大的影响,因此小波基的选择也是研究热点之一。如文献[16]设计了自适应小波特征的提取算法,文献[17]则通过构造新的小波优化目标函数,从而增强系统的鲁棒性。
本文利用的Gabor滤波器也是属于频域法。Gabor滤波器兼顾了时域与频域的选择能力,能提供良好的方向尺度选择特征。Mak提出了一种最佳的Gabor滤波器检测算法,该算法选择基于多通道和多尺度滤波图像的最佳Gabor滤波器[18]。此外,也有学者利用Gabor滤波器作为图像的预处理工具,并通过机器学习方法完成检测。
1.2.3 模型法
上述的统计法和频域法在织物的纹理规律性较强时有比较好的检测表现,但是当表面纹理含有较多随机成分时,这两种方法的应用空间并不大,而模型法则在随机场景下有较好的表现。
马尔科夫随机场模型可以用来描述像素间的相关性,同时考虑了图像的统计信息与结构信息。文献[19]比较了K-L马尔科夫随机场模型法的检测效果,在研究中,马尔科夫随机场模型在检测的实时性上表现更加突出。文献[20]中利用小波域马尔科夫随机场建立织物的纹理模型,模型的参数通过对于无缺陷图像的学习得到。实验对多种疵点图像进行了检测实验,结果验证了算法的可靠性。
从相关的文献中我们可以分析得到,马尔科夫随机场模型对于局部纹理特征具有优良的提取效果,但是易于忽略细小疵点的信息。
自回归模型利用了像素间的线性关系,从而打来线性预测的效果,在图像缺陷检测领域同样有一定应用。文献[21]提出了一种自回归模型来估计图像在频域中的能量密度,以克服传统频域算法检测速度和计算复杂度低的缺点。文献[22]提出的二维AR模型虽然也在检测上有一定的表现,但是比较容易受到噪声干扰,且对于光照条件的要求较为苛刻。文献[23]则进一步分析,认为AR模型仅在疵点表现为线状时有比较理想的检测效果,丰富了理论。
1.3 研究内容与预期目标
本文的研究围绕织物的缺陷检测进行,在纺织工业中,质量控制是其中的把关环节,而织物缺陷检测又是质量控制环节中的主要方面。由于人工检测存在着较大的缺陷,如工作效率低、检测标准受检测主体影响等等,所以用计算系统来代替人工进行工业检测是技术发展不可扭转的趋势。本课题是在对国内外相关领域的研究基础之上,利用数字图像技术,设计合适的算法,对常见的几种织物缺陷进行检测实验,从而达到利用机器视觉完成工业检测的目的。
因能力所限,笔者在研究过程中无法获得商业织物疵点数据集授权,如TILDA数据集的使用授权,本设计所用织物疵点图像均由笔者采集自互联网。设计的预期目标是设计的算法在几种常见的疵点图像上均能完成检测任务,不仅完成对于能否有疵点的判断,并且在图像上要具体定位疵点的位置,达到一定的自动化水平。
第2章 傅里叶变换
2.1 傅里叶变换原理
离散傅里叶变换(DFT)描述了离散信号在时域与频域的对应关系,是信号处于领域与线性系统分析中的一种常用工具,在图像处理领域应用很广。傅里叶变换是最为基础的从时域到频域的变换工具,从理解傅里叶变换的基础原理入手,有利于突出利用Gabor滤波器完成滤波操作的优缺点。
2.1.1 一维傅里叶变换
我们可以借助离散傅里叶级数,来研究一维离散傅里叶变换。
假设f(x)是在时域上采样得到的N点离散序列,F(u)是对应的频域变换结果,参数x是离散实变量,u为离散频率变量,则一维离散傅里叶变换的定义为:
(2.1)
上式为正变换公式,反变换公式同样可以推导如下:
(2.2)
2.1.2 二维傅里叶变换
图像是二维的信号,二维的傅里叶变换并不复杂,在一维傅里叶变换的基础上,如果我们对每一个行扫描线和列扫描线进行傅里叶变换,再依次叠加,就可以得到二维傅里叶变换的结果。
原始图像可以看成在现实空间中经过采样得到的一系列点阵,我们在计算机计算中习惯用矩阵表示图像信息,如z=f(x,y)。从傅里叶变换的直接效果上看,傅里叶变换的正变换是将图像从空间域转换到频域,而逆变换是把图像的频域信息返回到空间域。从数学角度看,正变换是将图像的灰度概率密度函数转换为频率分布函数,逆变换则是将频域分布函数转换为灰度分布函数。
二维傅里叶变换的正变换公式如下:
(2.3)
逆变换变换公式也可以通过推算得到:
(2.4)
其中x和y是离散实变量,u和v为离散频率变量。
另外可以将二维傅里叶变换的频谱(spectrum)和相位角(phase)定义为:
(2.5)
(2.6)
傅里叶变换中主要有三个分量编码,分别为频率,幅值和相位。一般在频域分析中,幅值表示图像明处与暗处的峰值差值,相位表示波形相对于原始波形的偏移量。频率表示图像中灰度变换的快慢程度,当频率很高时直观上表现为信号变化快速,频率较低时说明灰度变换较为缓慢,从观感上来说就是图像较为平滑。
图2.1与图2.2展示了用于演示的Lena图以及傅里叶变换,图2.3是原图在经过傅里叶正变换和逆变换后的结果。



图2.1 Lena图 图2.2 傅里叶变换图 图2.3 反变换图
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: