反常涡旋线偏振光束的紧聚焦特性毕业论文
2020-02-14 11:55:49
摘 要
涡旋光是具有螺旋相位波前和相位奇点的奇异光束,其具有奇特的环状光强分布以及非零的轨道角动量,在对粒子的微操作以及量子通信领域有着重要的应用价值。已得到了广大学者以及科研工作者的重视,成为光学研究领域中的一个重要分支。涡旋光束通过高数值孔径的透镜后有许多优异的性质,例如可以提高成像系统的分辨率,可对微粒进行捕获、加速与传输等。
本文以线偏振反常涡旋光为例,主要研究了其经过高数值孔径的透镜聚焦后,在焦平面处的光强和相位分布特性。理论推导了反常涡旋线偏振光经过高数值孔径的透镜后在深聚焦光场的表达式,分析了不同参数的改变对深聚焦场中光强及相位的影响。
研究结果表明:拓扑荷数对深聚焦场中光强分布的影响要远高于阶数,数值孔径越大的透镜对光束的聚焦作用越明显,在光束经过焦平面时,发生了由会聚波到发散波的转变,从而导致了相位的反转。
本论文的研究成果有助于进一步发现涡旋光束的潜在应用价值。
关键词:光学涡旋;紧聚焦;螺旋相位;光强分布
Abstract
Vortex light is a singular beam with helical phase wave front and phase singularity, which has a peculiar circular distribution of light intensity and non-zero orbital angular momentum. It has important application value in the field of particle micromanipulation and quantum communication. After passing through the lens with high numerical aperture, the vortex beam has many excellent properties, such as improving the resolution of the imaging system, capturing, accelerating and transmitting the particles.
In this paper, the anomalous vortex with linear polarization is taken as an example. Theoretically, the expression of anomalous vortex line polarized light in the deep focusing light field after passing through the lens with high numerical aperture is derived, and the influence of different parameters on the light intensity and phase in the deep focusing field is analyzed by using MATLAB numerical simulation.
The results show that the effect of the topology charge on the intensity distribution in the deep focusing field is much higher than the order. The larger the numerical aperture, the more obvious the focusing effect of the lens is. When the beam passes through the focal plane, the convergence wave becomes a divergent wave, which causes phase inversion.
The research is helpful to further discover the potential application value of vortex beam.
Key Words: Optical vortex; Deep focusing; Spiral phase; Intensity distribution
目 录
第1章 绪论 1
1.1 研究背景 1
1.2 研究目的及应用前景 2
1.3 本论文的研究内容及安排 4
第2章 理论基础 5
2.1 Debye矢量积分 5
2.2 切趾函数 8
2.3 涡旋光的概念及产生方法 11
第3章 反常涡旋线偏振光的紧聚焦特性分析 15
3.1 紧聚焦模型 15
3.2 数值仿真及分析 17
第4章 总结与展望 25
4.1 本文总结 25
4.2 展望 26
参考文献 27
致谢 29
第1章 绪论
1.1 研究背景
光有许多重要的性质,如反射、折射、干涉、衍射、偏振等等。光学已然成为人们生活中密不可分的一部分,学者对光学的研究也在逐日深入。而涡旋也是日常生活中非常普遍的自然现象,小到用勺子搅拌咖啡产生的涡旋,大到台风、龙卷风、飞机飞行时机身周围的大气旋涡。这种存在于自然生活中的现象都属于涡旋,他们的共同点就是都伴有波动现象,而且这种现象在日常生活领域都是可见的。从宏观上分析这种现象,我们所熟知的光波同样具有这样的性质,即涡旋性质。在自然界中,像光波这类属于电磁波的物质绝大多数都会伴有这种涡旋现象。涡旋光束是具有螺旋状等相位面和自身携带轨道角动量的光束,光束中心的相位不确定,存在相位奇异性,也称相位奇点,相位奇点处光强为零。在光学研究上,包括被大家所熟知的量子通信、光学成像都和螺旋相位结构有关,此外,具有涡旋性质的粒子所携带的轨道角动量特征也在光学研究中起着不可或缺的作用,这使涡旋光束在光学领域发挥着重要作用,例如在编码信息传输、图像加密、生物医学等等领域都有着极其重要的应用价值。
最早研究相位奇点并且推测出相位奇异性的是Whewell,这位学者在观潮之时巧妙地发现了这种奇妙现象,他灵敏的发现潮汐峰会存在一种特定的消失的条件,即当且仅当两条同潮线相对出现时[1]。1831年,将光学中的涡旋现象进一步深入研究下去是G.B.Airy,他发现了一个奇妙的现象,即在透镜的焦平面上存在一种特别的物质,该物质是一个奇异的光环,当发现这一现象之后,人们便开始初步研究光学中的涡旋现象[2]。1919年,Ignatovskii研究并分析了这个奇异光环周围的能流分布情况,研究发现该能流在自由空间中是沿着与初始方向相反的方向传播的[3]。1952年,Braunbek和Laukien做了一个实验,在半反射屏上以平面波入射,结果探索到了涡旋的存在,进一步证明,该涡旋是在发生干涉后的一个干涉场中出现的,而这个干涉场即是入射的平面波与其反射光形成[4]。1967年,Boivin、Dow、Wolf在非球面透镜系统中发现了有一个涡旋绕着焦平面旋转,这证明了光波场中也存在着涡旋[5]。20世纪70年代,通过不断的研究,相位奇点这一特征的提出显得尤为重要,随着后期进一步的实践证明,大家越发注重光学涡旋的作用,而相位奇点属于光学涡旋中一个最本质的特征,越来越在光学研究领域中占据重要地位。1974年,两位学者Berry和Nye通过研究进一步证明了产生光学涡旋的原因,这个原因就是存在相位缺陷。一般而言,经过反射后,那些粗糙表面多会出现相位奇点或相位断层的情况,这样就会造成相位缺陷,而这种常见的现象会给光束传播带来一定的负作用[6]。1979年,通过进一步的实验表明,某些光束间的分布结构是极其相似的,尤其是相位分布结构之间。通过分析比对拉盖尔高斯光束(Laguerre-Gaussian, LG)和涡旋光束,Vaughan和Willetts两位学者得出结论,这两种光束的相位分布结构非常相似[7]。1981年,Baranova等人证明了散斑场的作用,即在特定的领域内,能够带来光学涡旋。后续的实验进一步调研散斑场,经证实若想在其中产生具有高拓补荷数的光学涡旋场,几乎是不可能实现的[8]。直到1989年,Coullet等首次把“光学涡旋”这个专业名词引入学术界[9]。1992年,非线性介质的研究进一步推进,Swartzlander在此期间不仅提出涡旋光孤子的概念,而且对其在非线性介质中的传播情况也做了进一步的研究,发现很多奇妙的现象以及特有的性质。研究表明涡旋光孤子在非线性介质中传播时会有不同的性质,深入的研究表明,两者在特定情况下可以相互作用。这一发现也为后来提出新结论作了铺垫,包括光波传输的一些显著特征,其在两种不同条件下,即近轴和非近轴情况下传播时带有角动量这一系列特征等等[10]。1995年,在上述理论基础之上,He等人根据角动量理论的特性,在对光学涡旋的理论研究已经基本完备的条件下,也实现了对对微小粒子的研究,实验操作也证明其可行性以及可靠性,并使光学涡旋具有实际应用价值[11]。1997年,Simpson等人发现光学涡旋的轨道角动量可以传递给粒子,基于这一特性,可以使粒子发生转动,即“光学扳手”[12-13]。2004年,信号传输也极大推动了光学涡旋的研究[14]。2012年,E.Stankevicius等人进一步研究光学涡旋的性质以及将其性质拓展于MEMS领域之中,光学涡旋的研究进一步得到推动[16]。
我国开始关注并着手研究光学涡旋的时间比较晚,研究机构主要是一些高校和研究所,其中包括南开大学、北京理工大学、中国科学技术大学、四川大学、西安光学精密机械研究所等。其中南开大学在实验上实现了利用螺旋相位板来产生涡旋光束。北京理工大学探索并研究了涡旋光束在光学信息传输方向上的应用。中国科学技术大学探索研究了涡旋光束在微操纵以及在生物医学领域的应用。2008年,陈子阳,张国文等人利用平面波通过螺旋相位板产生了涡旋光,并用此涡旋光束做干涉实验,研究了干涉场中干涉条纹的分布情况[17]。2013年,反常涡旋光束被提出,其作为一种新的研究,大大推动了涡旋光束的发展以及后续工作的产生 [18]。2014年10月,Yuan研究了反常涡旋光束通过环形光阑以及在湍流大气中的传输特性[19]。2014年11月,Zhang研究了反常涡旋光在光镊上的应用[20]。
1.2 研究目的及应用前景
涡旋光束是一种具有螺旋相位波前结构和轨道角动量的奇异光束,并且存在相位奇点。尽管很早之前就已经提出光学涡旋,但仅根据当时的条件,人们没有做进一步的研究。直到后来,涡旋光束的理论研究与实际应用才开始重新得到科学家们的重视,尤其是近年来科学家和学者们对涡旋光的广泛关注和研究。由于涡旋光束这些特有的性质,使其具有不可估量的潜在应用价值。涡旋光束特有的拓补荷数为整数阶时,可用于更加稳定地进行信息编码和信息传输,利用涡旋光束,可以实现更高的机密性和更快的传输速度。在通信领域,涡旋电磁波有望为扩大手机、数字电视和互联网通信的可用带宽做出重大的贡献。这将极有力地推动通信技术的未来发展,为进一步拓宽通信市场打下了良好的基础。另一方面,光学涡旋在微操纵领域已有了较为可观的发展,不同于传统的接触式捕获,利用涡旋光束的梯度力和散射力之间的平衡关系,可对微小粒子进行捕获、移动和旋转,不需要直接接触粒子,免除了不必要的物理损伤。在生物医疗领域,这种技术对于操控微小原子、细胞、染色体等的优势极为明显,即无损伤,更精确。在癌细胞研究、细胞新陈代谢及物理学上对粒子的研究等具有极为重要的应用价值。涡旋光束经高数值孔径的透镜聚焦后,在聚焦场能够获得比普通聚焦光斑尺寸更小的光斑,可以有效提高成像系统的空间分辨率。因此,研究涡旋光束深聚焦场的分布特性,可以帮助我们更好的掌握光的偏振,有助于我们进一步深刻地理解光的本质,对光学未来的发展及应用有着极其重要的意义。
利用涡旋光束对微小粒子进行操控是一门新兴技术,这种技术被称为“光镊”或“光学扳手”,有着非常可观的发展前景。根据之前的多项研究,微小的粒子的研究已经成熟,而在这些应用中也能很好的发挥特有的功能,但是面临的难点是,而这些微粒一般是微米或纳米量级,普通的器械难以对其进行捕获或者操控。而“光镊”或“光学扳手”这种现代技术的出现,正好解决了这个难题。不同于以前,这种技术是利用聚焦方法,微粒置于这种聚焦场中,将会受到梯度力与散射力的作用,因此会被束缚于透镜的焦点处。由于涡旋光自身携带的轨道角动量可以传递给被捕获粒子,可以实现对粒子的转动操作。利用涡旋光进行捕获的技术于传统技术而言有着极大的优势,利用力的平衡作用来实现对微粒的控制,这种非接触式的操作方式无机械损伤,能更好地保护如细胞这类的生物活体粒子。不仅如此,光学涡旋还可以筛选不同大小的微粒,能进行微粒的重组。在生物医学领域,光镊技术可以进行染色体的微切割和片段收集,对原生质体的融合等等。总的来说,基于光学涡旋的微操纵技术所具有的零接触、零损伤、灵活性高、可操作性强等优点,具有广阔的应用前景和应用价值。
在通信领域,利用涡旋光束的轨道角动量,可以实现信息编码和信息传输。这种通信技术保密性更强、安全性更高,具有无可比拟的优势。在信息编码与信息传输过程我们一般用到角动量,而这种编码方式会有一定的散射作用,该作用会影响涡旋光束的结构,而且在编码时这种散射作用的出现对其造成的变化也是一个随机过程。因此,对散射光进行分析,并提取出轨道角动量的信息,得到信息编码时正确的排列组合,几乎是不可能的。这就大大增加了窃取信息的难度。其次,轨道角动量的大小与拓补荷数相关,而拓补荷数可以为任意数值,所以拓展了通信系统的容量,使其可以存储更多的信息。另外,研究发现,光学涡旋所具有的量子纠缠效应,在浓缩编码、纠错码、量子计算等量子通信领域也有着极为可观的发展前景。
1.3 本论文的研究内容及安排
本论文对反常涡旋线偏振光束经过高数值孔径的透镜后的紧聚焦特性进行了深入研究,推导出了反常涡旋线偏振光的在紧聚焦场的光场分布函数,对理论研究的成果进行了仿真验证,得出了紧聚焦场的光强及相位分布特征,论文的主要内容如下:
第1章,绪论。结合对相关参考文献的阅读和理解,介绍了涡旋光束的概念以及一些基本特征,了解了涡旋光束在国内外的研究背景以及应用前景,明确了本论文的研究目的及内容。
第2章,基础理论介绍。介绍了本论文需要用到的基础理论,Debye衍射积分与切趾函数,明确深聚焦的含义,讨论分析了在不同的近似条件下,通过高数值孔径的透镜后,反常涡旋线偏振光束在聚焦场中的光强表达式。
第3章,反常涡旋线偏振光的紧聚焦特性的研究。理论推导出线偏振反常涡旋光经过高数值孔径的透镜后在在不同传播方向上的电场分量,利用MATLAB进行数值分析,研究拓扑荷数和阶数的改变对光场以及相位的分布有何影响。改变传输距离z,研究不同的传输距离所在的平面处光强和相位分布有着怎样的不同。再改变透镜数值孔径的大小,讨论不同聚焦能力的透镜对线偏振反常涡旋光深聚焦场的光强分布具有怎样的影响。
第4章,论文的总结与展望。对此次论文的研究内容进行总结以及展望未来工作内容,提出不足之处和可以进一步进行改进的地方,揭示涡旋光束对未来科学技术发展中的巨大潜力,其次,对在完成本篇论文的过程中帮助过我的老师及同学们表达诚恳的感谢。
第2章 理论基础
2.1 Debye矢量积分
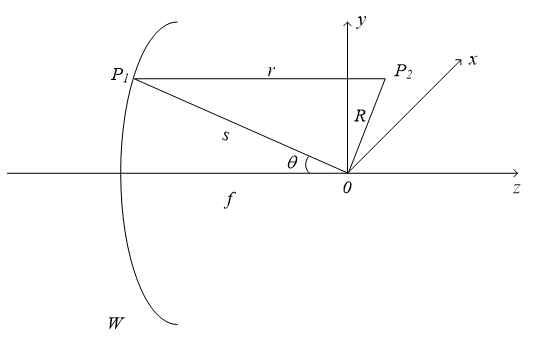
图2.1 球面波聚焦光路图
图2.1是一束球面波经透镜聚焦后的衍射模型,其中W是此球面波的波前,O是透镜的聚焦点,将此处设为原点。可得到球面波前W上的一点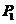 的复振幅为
的复振幅为
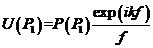 (2.1)
(2.1)
其中f是透镜的焦距,也是球面的半径。表达式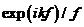 意味着一个球面波汇聚于O点。在一般情况下,球面波前的场并不是一个常数,这里我们引用
意味着一个球面波汇聚于O点。在一般情况下,球面波前的场并不是一个常数,这里我们引用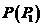 来表示球面波前的场分布,在这种分布情况下,我们可以得到球面波经透镜聚焦后在聚焦场中对应的
来表示球面波前的场分布,在这种分布情况下,我们可以得到球面波经透镜聚焦后在聚焦场中对应的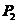 处的场分布为[21]
处的场分布为[21]
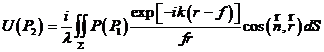 (2.2)
(2.2)
我们可以引入如下的近似条件来对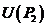 进行简化:
进行简化:
近似条件一:在衍射光阑处,我们把原始的微小球面波逐渐逼近于微小的平面波。所以观察到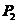 与焦点O之间的距离差可近似为
与焦点O之间的距离差可近似为
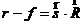 (2.3)
(2.3)
其中,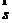 向量表示焦点O到入射点
向量表示焦点O到入射点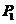 的单位矢量,向量
的单位矢量,向量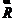 表示焦点O到观察点
表示焦点O到观察点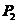 之间的单位矢量。
之间的单位矢量。
近似条件二:
 (2.4)
(2.4)
其中,dS表示一个微小的面元,d表示这个面元所对应的微小的空间立体角。
近似条件三:方向余弦可以近似为
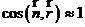 (2.5)
(2.5)
其中,向量表示衍射光阑的法向单位矢量,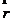 向量表示球面波上一点
向量表示球面波上一点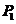 指向经透镜后聚焦场中的对应观察点
指向经透镜后聚焦场中的对应观察点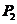 的单位矢量。
的单位矢量。
近似条件四: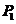 与
与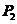 之间的距离r可近似于与焦距f相等。
之间的距离r可近似于与焦距f相等。
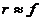 (2.6)
(2.6)
综合上述四个近似条件,讲表达式(2.3)和(2.6)代入(2.2),可以将(2.2)化简为
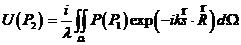 (2.7)
(2.7)
式(2.7)被称为Debye积分[3],上述四个近似条件被称为Debye近似。
当聚焦系统为圆透镜时,我们以焦点O作为原点建立球坐标系,可以得到球面波上任意一点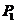 的坐标为
的坐标为
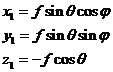 (2.8)
(2.8)
其中
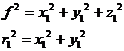 (2.9)
(2.9)
再以O点为原点建立极坐标系,则观察点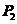 的坐标为
的坐标为
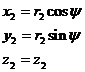 (2.10)
(2.10)
其中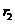 满足关系式
满足关系式
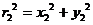 (2.11)
(2.11)
根据正弦定理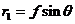 ,再结合公式(2.3)、(2.4)、(2.5)和(2.6)这四个Debye近似条件,有
,再结合公式(2.3)、(2.4)、(2.5)和(2.6)这四个Debye近似条件,有
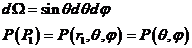 (2.12)
(2.12)




