自适应滤波算法的研究及Matlab实现毕业论文
2020-04-12 08:48:26
摘 要
自适应滤波算法性能的优劣直接影响着自适应信号处理的结果,故在自适应信号处理领域中,算法的研究是重中之重。本文对自适应滤波技术的基本原理进行概述,重点开展了对以维纳滤波理论为基准提出来的LMS算法的研究。
文章在论述传统LMS算法基本原理的基础上,对算法性能的衡量指标开展学习,并针对传统LMS算法存在的不足,结合参考文献的介绍,以提升传统LMS算法的性能为目标,学习和研究了归一化LMS算法、基于Sigmoid函数的SVS-LMS算法和基于Sinh函数的Sinh-LMS算法等变步长LMS算法。
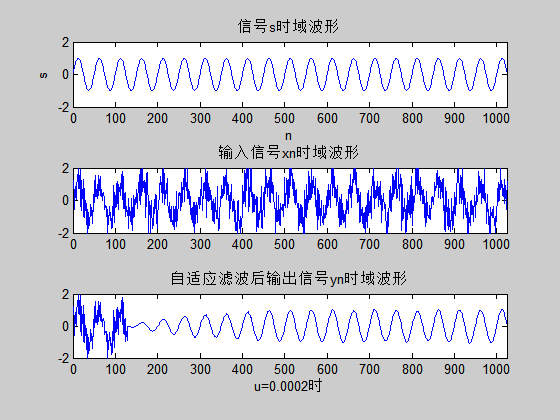
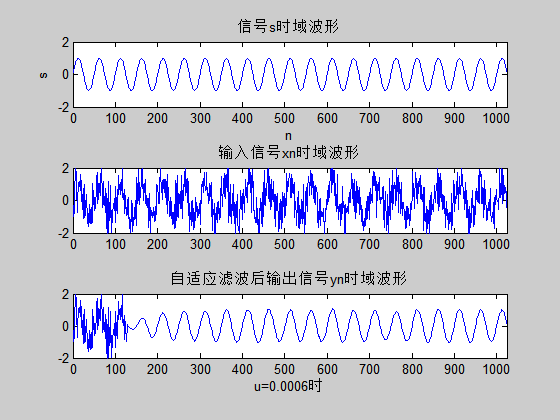
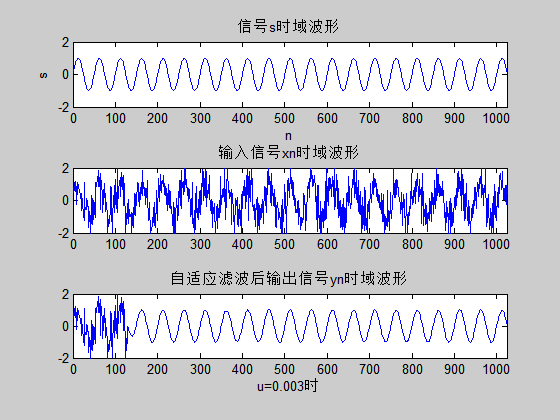
最后借助MATLAB软件对本文研究的传统LMS算法及改进型算法进行仿真,论证本文介绍的三种改进型LMS算法均能在保证系统稳态误差的前提下,提升算法收敛速度,整体性能有了很大的提高。
关键词:自适应滤波;LMS算法;NLMS算法;Sigmoid函数;双曲正弦函数
Abstract
The performance of adaptive filtering algorithm directly affects the result of adaptive signal processing, so the research of algorithm is the most important in the field of adaptive signal processing.This paper summarizes the basic principle of adaptive filtering technology, and focuses on the research of LMS algorithm based on Wiener filtering theory.
On the basis of discussing the basic principle of traditional LMS algorithm, this paper studies the performance measurement of the algorithm.And aiming at the shortcomings of the traditional LMS algorithm, combined with the reference, in order to enhance the performance of the traditional LMS algorithm as the goal.Then we study the variable step LMS algorithm such as NLMS algorithm, SVS-LMS algorithm based on Sigmoid function and Sinh-LMS algorithm based on hyperbolic sine function.
Finally,the traditional LMS algorithm and the improved algorithm are simulated by MATLAB software. The three improved LMS algorithms presented in this paper can improve the convergence speed of the algorithm under the premise of ensuring the steady-state error of the system, and the overall performance has been greatly improved.
Key Words: Adaptive filtering; LMS algorithm; NLMS algorithm; The Sigmoid function; Hyperbolic sine function
目 录
第1章 绪论 1
1.1 课题研究背景及意义 1
1.2 国内外研究现状 2
1.3 本文主要研究内容 3
第2章 自适应滤波器及其算法原理 4
2.1 自适应滤波器的基本原理 4
2.2 自适应滤波算法的理论研究 5
第3章 最小均方(LMS)算法的研究及实现 7
3.1 维纳滤波 7
3.2 最陡下降法 8
3.3 最小均方(LMS)算法 9
3.3.1 LMS算法描述 9
3.3.2 LMS算法的收敛性 11
3.3.3 LMS算法的收敛速度 11
3.3.4 LMS算法的期望学习曲线及性能 12
3.4 LMS算法的仿真实现 13
第4章 改进型LMS算法的研究及实现 17
4.1 归一化LMS算法 17
4.1.1 归一化LMS算法的基本原理 17
4.1.2 归一化LMS算法的仿真实现 18
4.2 基于Sigmoid函数的SVS-LMS算法 20
4.2.1 SVS-LMS算法的基本原理 20
4.2.2 SVS-LMS算法的仿真实现 21
4.3 基于双曲正弦函数的Sinh-LMS算法 24
4.3.1 Sinh-LMS算法的基本原理 24
4.3.2 Sinh-LMS算法的仿真实现 25
4.4 传统LMS算法与改进型LMS算法的比较及分析 27
第5章 总结与展望 30
5.1 本文工作总结 30
5.2 展望 30
参考文献 32
致 谢 33
第1章 绪论
自适应滤波理论作为信号处理的重要构成部分,是主要研究一类结构和参数可以改变或者调整的系统[2]。在实际生活应用中,实际信号系统往往随着时间和空间的变化而不断变化,信号的统计特性是未知不定的,在这种情况下,必须要求滤波系统的参数能随环境的变化而自行调整,达到最佳滤波,这便是自适应系统。自适应系统它可以通过自学习来适应信号传输变化的环境和要求,它可以在信号的结构性质等知识均为未知的情况下,在工作过程中根据外部环境的变化,自动调整系统的参数,以达到最佳滤波效果。因此自适应系统能极大的保证信号的不失真,更快更好的解决复杂信号的处理问题,是智能信息处理的重要基底!本文在论述自适应滤波技术原理的基础上,深入学习自适应滤波算法,并以LMS自适应滤波算法为例开展仿真研究。
课题研究背景及意义
自适应信号处理正是由上个世纪20年代通信领域中提出的优化理论发展而来[1]。1942年,维纳研究了基于最小均方误差准则并利用Wiener-Hopf方程给出了对连续信号情况的维纳解,后来人们以最小均方准则为基底所设计出了维纳滤波器[2]。直到1960年,随着空间技术的进步,卡尔曼在提出了基于最小均方误差的对于非平稳随机序列的离散形式递推算法,这便是著名的卡尔曼滤波算法[2]。以这两种算法设计而来的滤波器但仍需要事先知晓输入信号和噪声信号的统计特性才能得出最优解,但事实上,这些先验知识是难以事先知晓的。故在未知系统环境、未知信号统计特性的情况下能实现最佳滤波的自适应滤波器便应运而生!
Widrow.B等于1967年提出了继承了维纳滤波器便于实现和卡尔曼滤波器优异的滤波性能的自适应滤波理论,它去其糟粕解决了两者需要事先知晓信号的统计特性的这个缺点,在工作过程中面对未知情况或者变化的环境时,也能通过自动调整参数以满足某种优化准则,实现最佳滤波。随着技术的飞速发展,自适应滤波技术在四十年来获得了巨大的发展和十分广泛的应用,成为最活跃的研究领域之一。它不仅在微石英音叉陀螺信号的解调应用中展现出的零位稳定性和分辨率[10],它还可以用来检测平稳和非平稳的随机信号,是智能信息处理的重要基础,在通信、雷达、图像处理、地震勘测和生物医学工程等方面有着十分广阔的施展空间[1][3]。
自适应滤波算法算法的性能直接决定着滤波器的性能,故对自适应滤波算法的研究是重中之重。Windrow和Hoff于1959年提出的最小均方(LMS)自适应滤波算法极大的推动了自适应信号处理技术的发展[2]。LMS自适应滤波算法通过不断的调整系数,依据参数变化修改权系数以达到使输出误差序列的均方值最小化的目的,满足最小均方准则[7]。而它能成为所有自适应滤波算法中拥有最广阔的应用空间的算法离不开其结构简单、计算量小和易于实现等优点。收敛速度、稳态误差及抗噪声干扰能力是评估算法优劣的重要指标[1]。正是因为传统LMS算法难以同时满足收敛速度和失调量这两项指标,人们在此基础上发展出多种算法:量化误差算法、变换域LMS算法、变步长LMS算法、变阶数LMS算法等[3]。此外,针对在实际研究发现的特定问题,又提出了一系列改进算法。如基于凸组合的并联LMS滤波算法(CLMS),还如基于CLMS提出的改进算法:基于变步长的CLMS算法(VSCLMS)等等[9]。
而以最小乘法(LS)提出的递推最小二乘算法(RLS)在自适应滤波算法中也占据着重要地位,标准的RLS算法是由Plackett与1950年首次提出。它是一类快速算法,有两个方面的内容:时间递归最小二乘算法(TRLS)和阶数递归最小二乘算法(ORLS)[3]。总的来说,它有着比较快的收敛速度,在实时系统识别和快速启动的信道均衡等方面有着广泛的应用。但因为LMS自适应滤波算法相较于其他算法而言优点过于突出,LMS及其延伸改进算法的研究仍拥有很大的热度。
结合相关文献并综上所述,自适应滤波技术具有自学习、自跟踪、对参数不定的动态系统拥有良好的滤波效果,我们有必要对其进行深入的学习和研究[15]。而从目前的研究情况来看,自适应滤波技术能发展到今天的水平要归功自适应滤波算法的发展,对于算法的性能的研究,和如何改进算法,至今仍是我们不断追寻的重点方向。而LMS的提出和发展对自适应滤波算法的进展做出了巨大的贡献,因此以最小均方准则提出的LMS自适应滤波算法的研究具有十分重大的意义!
国内外研究现状
说到自适应滤波技术就必然绕不开20世纪40年代提出的维纳滤波理论和1960年提出的卡尔曼理论,虽然它们在实际应用中有着致命的束缚,但是它们的出现为自适应滤波算法提供了一个标准。在上个世纪50年代,P.Howells在研究制作天线的过程中首先提出了自适应滤波的概念,而维德罗和Hoff于1959年提出的最小均方(LMS)自适应滤波算法奠定了自适应滤波的理论基础[11],对后来各式自适应滤波算法的成长和研究有深远的意义。随即,D.Gabor等人研制出了自适应滤波器。在这之后,在维纳滤波理论和卡尔曼滤波理论的基础上推得的新算法层出不穷。同年,Reed等人首先系统的讨论了采样矩阵求递(SMI)算法,可以实现很高的处理速度,在雷达系统中有着广泛的应用[2]。到了八十年代,McWhirter提出了RLS算法,Ward和McWhirter在这一基础上进一步推出高稳定性、可用Systolic处理结构高效率实现的QR分解RLS算法[2]。而Sayed等人于1994年在将卡尔曼滤波的大量研究成果应用于自适应滤波处理后,从而建立的卡尔曼滤波和递推最小二乘算法之间的对应关系,更是对自适应滤波技术的发展起了重要的推动作用。
LMS自适应滤波算法结构简单、低计算复杂度、在平稳环境中的良好收敛性、算法在有限精度下的稳定性,使其成为自适应滤波算法中应用最广泛的算法,但其自身的收敛速度和稳态误差仍旧存在着不可调和的矛盾。针对这一现状,近年来国内外以传统LMS自适应滤波算法为基底研究发展出了多种改进型的LMS算法。如归一化LMS算法,Herzberg等提出的延时LMS算法,Kwong于1992年提出的通过瞬时误差的平方控制步长的变步长LMS算法,以及基于双曲正切、三角函数等多种函数提出的变步长LMS算法[11],1996年提出的将步长因子和误差信号拟合于Sigmoid函数的SVSLMS算法[6],2001年提出的分割滤波器算法和2005年提出的分数阶速算法等等[12]。这些改进算法的出现在一定程度上提高了自适应滤波器的滤波效果。由此可见,LMS自适应滤波算法在自适应滤波算法中所占的重要地位,而它的研究从未松懈。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: