基于RLS(递归最小二乘)算法的滤波器研究与实现毕业论文
2020-02-17 23:13:14
摘 要
自适应滤波器在现实的应用普遍,在通讯、人工智能、雷达、导航等许多行业内都有所应用。自适应滤波器是在未知的条件下,通过自己的对外部环境的统计,可以自动的调节自身的数值,以满足到适应环境的条件。正是自适应滤波器的这种特性,也是他的优点,使得它可以在诸多环境使用,并且有着很好的应用效果。
本文是从自适应滤波器的研究背景及课题的研究意义开始着手,介绍了自适应滤波器的主要原理,自适应滤波器的算法主要包括LMS(最小均方误差)算法和RLS(最小二乘)算法,其中具体的阐述了RLS(递归最小二乘)算法的原理及推导过程。在理解上述自适应算法的基础上,采用matlab软件进行仿真,对两种算法的滤波效果进行了对比,也通过改变滤波器阶数和遗忘因子来讨论对滤波效果的影响。两种滤波器的滤波效果,RLS自适应滤波器是优于LMS滤波器的。滤波器的阶数越高,滤波器的滤波性能就越好。遗忘因子需要在0到1的范围内改变,当遗忘因子接近1时,滤波效果越好。
关键词:自适应滤波器;RLS算法;matlab
Abstract
Adaptive filters are widely used in many fields, such as communication, artificial intelligence, radar, navigation and many other fields. The adaptive filter is able to automatically adjust its own parameters in a positional environment through its own statistics on the external environment to meet the requirements of the environment. It is this characteristic of the adaptive filter that is also his advantage, which makes it usable in many environments and has a good application effect.
This paper starts with the research background and significance of adaptive filter, and introduces the main idea of adaptive filter. The algorithm of adaptive filter mainly includes LMS (least mean square error) algorithm and RLS (least squares) algorithm, among which The principle and derivation process of the RLS (Recursive Least Squares) algorithm are described. On the basis of understanding the above adaptive algorithm, the simulation is carried out by using matlab software, and the filtering effects of the two algorithms are compared. The influence of filtering effect is also discussed by changing the filter order and forgetting factor. The filtering effect of the two filters, the RLS adaptive filter is better than the LMS filter. The larger the order of the filter, the better the filtering effect. The forgetting factor needs to be changed from 0 to 1. When the forgetting factor is close to 1, the filtering effect is better.
Keywords: adaptive filter; RLS algorithm; matlab
目录
摘要 I
Abstract II
第1章 绪论 1
1.1论文的研究背景 1
1.2课题研究意义及目的 1
1.3论文研究内容及结构安排 2
第2章 自适应滤波器原理 3
2.1RLS滤波器原理 4
2.1.1预备知识 4
2.1.2RLS算法推导 7
2.1.3算法的计算过程 8
2.2LMS算法原理 10
2.2.1LMS算法计算过程 10
2.3本章小结 11
第3章 实验结果与分析 12
3.1matlab简介 12
3.1.1 Matlab特性 12
3.2实验仿真及代码实现 13
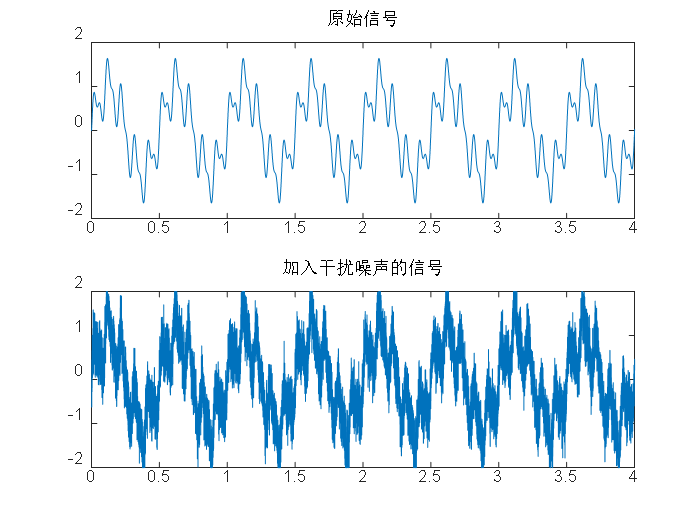
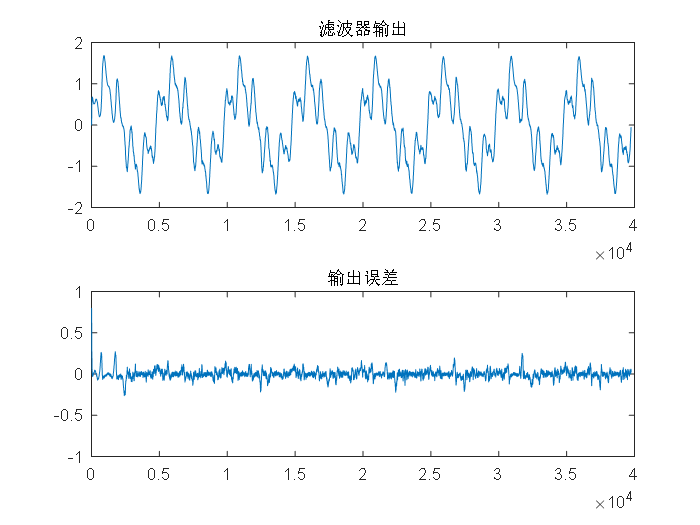
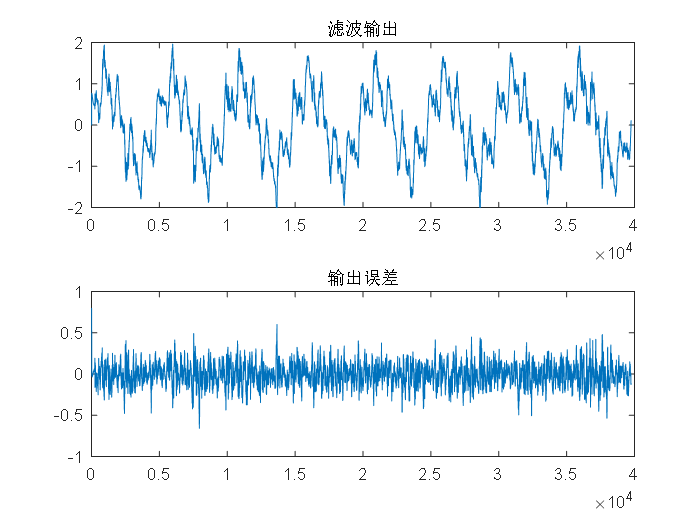
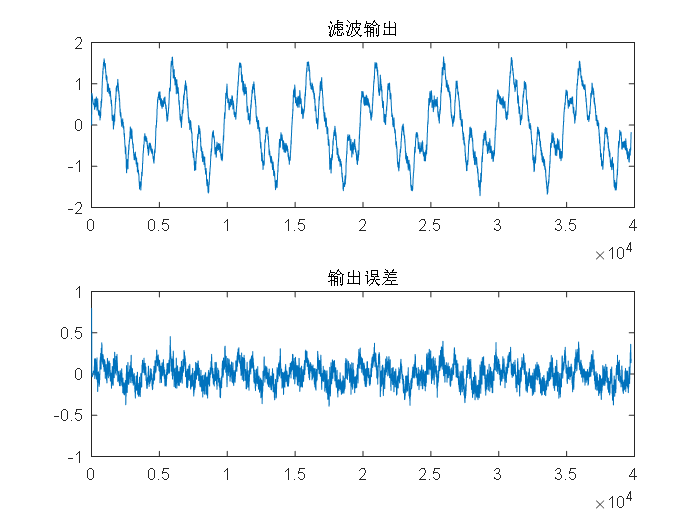
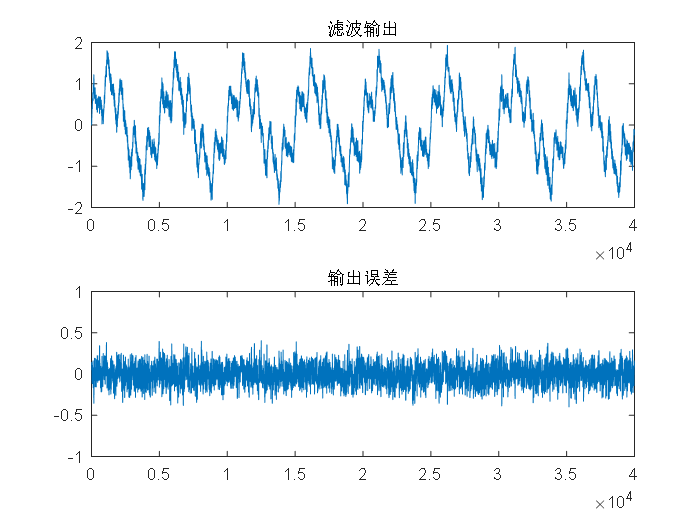
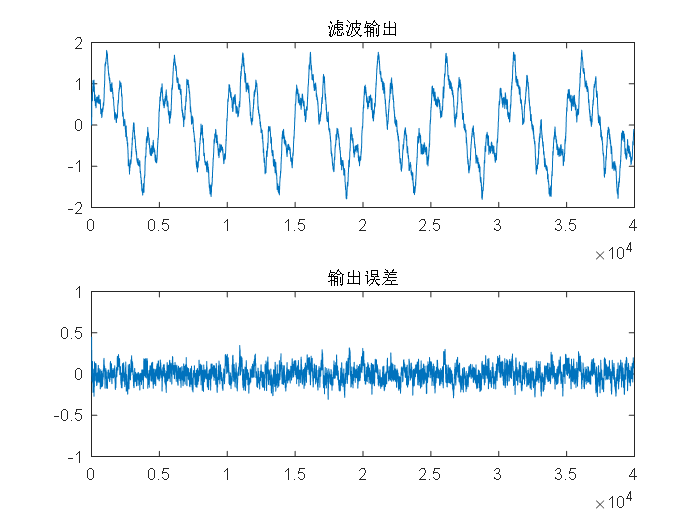
3.2.1RLS算法与LMS算法的实验对比 13
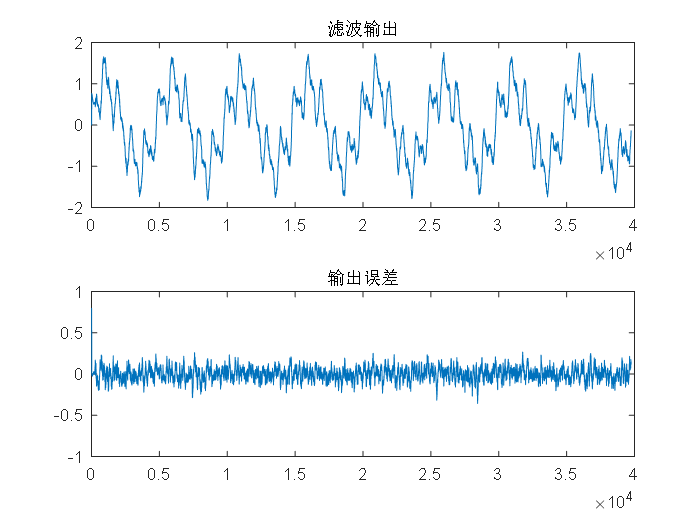
3.2.2改变遗忘因子的RLS自适应滤波器 16
3.2.3改变滤波器长度的RLS自适应滤波 18
3.2.4改变输入信号的RLS自适应滤波 20
3.3本章小结 22
第4章 总结与展望 23
4.1总结 23
4.2展望 23
参考文献 24
附录: 25
致谢 29
第1章 绪论
1.1论文的研究背景
自适应信号处理就是一种可以自身变化或者可以自己调整自身参数的系统,可以对外部环境的因素的反馈处理来改善对信号的处理的能力。通常这种系统为非线性系统,通过对系统通道的设计,自动的适应外界环境的变化或要求。例如一个自适应滤波器的输入信号不包含噪声信号,这个自适应滤波器可以等效为全通滤波器,如果输入为有用信号加噪声信号,就可以等效为普通的滤波器。自适应滤波器的特点是取决于其滤波过程。
自适应滤波器通常用来从含有噪声的信号中提取有用信号。在这个应用下,自适应滤波器已经普遍使用在芯片、语音处理、自动控制等许多领域。
对递归最小二乘自适应滤波器,我们发现Plackett算法已经与标准的 RLS算法十分接近了,虽然也有许多其他许多研究者推导或者重新推导了各种形式的RLS算法。1974年,戈达尔在卡尔曼滤波器理论的基础上推导出了一种改进的新型算法,有时在文献中被为戈达尔算法。之前,已经许多研究者已经应用卡尔曼滤波器理论解决自适应滤波器问题。后来,Sayed和Kailath一起发表了一篇论文,第一次提出了建立RLS算法与卡尔曼滤波器理论之间的关系,它为如何使用卡尔曼滤波器理论处理线性自适应滤波器问题打下了基础。
微电子技术和集成电路的快速发展促进了自适应滤波器的研究与发展。自适应滤除语音信号中的噪声的研究大概开始于1965年。贝尔电话实验室的Kelly首次把自适应滤波器应用于消除回声,这是语音信号采用自适应算法处理的开端。Kelly的贡献为Sondhi的论文所认同。该发明及改进体现在Kelly和Logan和Sondhi的专利中。
由Widrow及研究同事一起研发了自适应谱线增强器,进一步的扩大了自适应噪声消除在应用中的使用。
尽管自适应回音消除器和自适应谱线增强器是两个不同的器件,但都可以作为Widrow所称的自适应噪声消除器的应用实例。
1.2课题研究意义及目的
信号处理的基本方法和原理是滤波技术,其中特别是数字滤波技术在诸多领域得到了普遍的使用。数字滤波理论的研究以及相关产品的开发引来了越来越多的国家的关注。
现在在自适应信号处理的研究中对自适应滤波算法的研究最为热。Windrow在1967年提出的自适应滤波系统的概念,其参数可以自动调节以达到最佳的系统性能,而在滤波器的设计中,很难会有关于信号和噪声的先验知识。该滤波器的算法实现简单,滤波器的性能也与卡尔曼滤波器不分伯仲。相比普通的滤波器而言,自适应滤波器的输出信号或滤波器的抽头系数是随着外界环境的变化而自己变化。经过一段自我调整的时间后,可以达到最优的滤波器性能。所以,自适应数字系统的显著特征有:自我学习能力强、算法简单和自我跟踪能力强。
自适应滤波算法的核心难点是如何提升或者改进自适应算法的性能。现在所研究出来的自适应算法有最小均方自适应算法和递归最小二乘自适应算法及其相关的改进算法,例如归一化( NLMS)算法、QR-RLS算法等,这些算法各有优劣,可以根据要求应用于不同的环境。由于基于最小均方误差准则的自适应滤波算法的收敛性比较差,在自我调节的过程中的反应比较慢。为了克服LMS算法的缺点,我们采用每次输入信号与输出信号之间的平方误差之和最小的方法,即RLS算法。 RLS算法的复数乘法与RLS算法的复数乘法成正比,使其自适应速度更快。目前,系统识别,噪声消除,自适应谱线增强,自适应信道均衡,语音线性预测,语音处理,自适应天线阵列等许多领域都已经广泛应用的RLS算法。
1.3论文研究内容及结构安排
本篇论文所研究的是RLS(最小二乘)算法的matlab实现,讨论了RLS自适应滤波与LMS自适应滤波的性能好坏,单独的研究了遗忘因子的改变、自适应滤波器阶数的改变和不同信号的输入对RLS自适应滤波性能的影响,通过对实验结果的分析得出相应实验结论。
对于本篇论文的结构安排:
- 第一章是绪论部分。对论文的研究背景和课题的研究意义做出来简单阐述。
- 第二章是对自适应滤波原理的介绍。首先简单的介绍了自适应原理,紧接着对RLS自适应算法进行详细的推导,最后是对LMS算法的粗略分析,在对本章进行小结。
- 第三章是实验结果与分析。首先简单的介绍了matlab软件,之后就是对实验的结果图进行分析并得出结论,再进行本章小结。
- 第四章是总结与展望。总结是对本次毕业设计内容的简单概括,展望是对今后的学习和工作上的帮助。
第2章 自适应滤波器原理
适应滤波器的主要组成部分有:自适应滤波算法和可以调节自身参数的滤波器。可变参数的数字滤波器可以选择有限长数字滤波器或无限长数字滤波器,也可以选择格型数字滤波器。输入信号通过可变参数的数字滤波器后产生输出信号,将其与参考信号进行比较相减,可以得到误差信号。有的时候还要利用某种自适应算法对滤波器抽头系数进行优化,最终使得输入输出均方差达到最小。所以,简单来说,自适应滤波器就是一个可以随外部环境变化可以自动调节自身参数的维纳滤波器。在设计滤波器的时候是不需要事先知道输入信号和噪声的先验知识,它可以在自身的滤波过程中慢慢了解相关的统计特性,可以根据外部因素的变化自己估计需要的知识,并且以此为依据自动的调节自身的抽头系数,以达到最佳的滤波性能。如果输入信号发生改变,滤波器自身可以自动的抓取这个改变,自动的调节滤波器参数,使滤波器性能够再一次达到最优。但是,尽管有这个特性自适应滤波器还是有线性和非线性两个分类。只要输入输出之间的关系是一一映射的,则这个滤波器会被认为是线性滤波器;否则,认为滤波器是非线性。
在自适应算法中,其影响因素多取决于如下的一个或者多个因素[1]:
(1)收敛速度。其定义为算法在输入信号为平稳信号时,能够最大限度的减少达到优维纳解所需要的迭代数。 。
(2)失调。对于一个有趣的算法,该参数为自适应滤波器组平均值的最小均方误差和维纳滤波器的最小均方误差之间的差值提供了衡量的标准。
(3)跟踪。当自适应滤波算法运行在非平稳环境中,该算法会随着外部环境的变化而自动的调整。但是,算法的自我调整的性能取决于两个相互排斥的因素,第一个是收敛得快慢,第二个是由算法噪声所造成的误差。
(4)鲁棒性。就鲁棒自适应滤波器而言,一个小的波动就会导致小的输出误差。这些干扰是由滤波器的各种外部因素和内部因素引起的。
(5)计算要求。需要关心得问题有,一次迭代所需要的运算量(加法、减法、乘法和除法),还有存储数据和程序所需要的存储空间大小,最后就是,计算机编程所需要的时间。
(6)结构。主要是指硬件的实现架构。
(7)数值特性。在实现算法过程中,量化误差会产生一定的不确定性误差,该误差主要是由输入信号的模数转化过程中和内部数据处理过程中所产生的。一般来说,后者的量化误差会造成严重设计问题。对于数值特性所关心的基本问题有两个,一个是数值稳定性,另一个是数值精确性。
只要维纳滤波器只有一个确认的参考结构,以上的这些影响因素就还会以其特殊方式影响着非线性自适应滤波器的设计,此外,非线性滤波算法也可能收敛于一个极小点。
2.1RLS滤波器原理
RLS算法可以看成是维纳滤波器的另一种表示形式。其实质上,维纳滤波器是从集平均推导出来的,其结果是一种在统计意义上的最优的、可以在各种环境下很好适应的滤波器;并且假设滤波器所在的外部环境是平稳的,除此之外,可以认为RLS算法是确定性的。具体来说就是,因为它采用的是在时间上进行平均,所以,在计算中所使用的样本因素决定了滤波的结果如何。在计算过程中,由于最小二乘法是用来处理批量的输入数据,所以最小二乘法是一种批处理方法。RLS自适应滤波器算法是对前一数据的计算处理可以递归得到处理后一个数据的有用信息,这样可以处理非平稳的信号。也正是以为如此,RLS算法的运算量要远远大于LMS自适应滤波算法[3]。但是,由于现在计算机的计算能力越来越强,在计算能力上的问题已经不再成为了阻碍了,所以这种批处理方法也变得越来越具有吸引力。
2.1.1预备知识
定义代价函数为ζ(n),其中n是定义的可变参量,需要在ζ(n)中引入加权因子[2]。可以得到下式
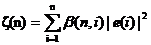 (2.1)
(2.1)
其中e(i)是为i时刻的期望响应d(i)与i时刻抽头输出y(i)的差值,e(i)如下所示,即
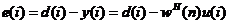 (2.2)
(2.2)
其中u(i)是i时刻的抽头输入向量,其表达式为
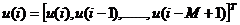 (2.3)
(2.3)
其中W(n)是n时刻的抽头权向量,其表达式为
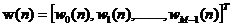 (2.4)
(2.4)
在代价函数中的加权因子ß(n,i)[7],需要满足如下关系
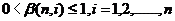 (2.5)
(2.5)
将加权因子,这里被称为的遗忘因子,定义为
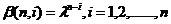
在式中的λ趋近与1,且小于1的正常数。当λ=1时,对应一般的最小二乘法。
输入信号u(i) u(i-1) u(i-M 2)
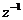
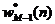
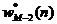
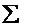
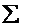
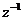
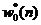
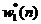
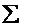
.....
....
u(i-M 1)
输出
y(i)
图2.1横向滤波器
首先需要了解最小二乘估计的病态特性的原因:
1.输入数据信息不足以构建输入输出之间一一对应的映射关系。
2.输入数据存在不可消除的噪声或者其他的干扰因素,这也增加了输入输出之间映射的不唯一性。
为了解决病态特性,需要输入与输出之间的某种先验信息,用来反映输入输出的映射关系。所以这就需要将先验知识加入代价函数,用以解决病态特性。
由此我们可以把扩展的代价函数分为误差加权平方和和正则化项[4]
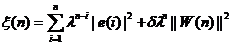 (2.6)
(2.6)
(1)误差加权平方和
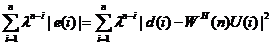 (2.7)
(2.7)
这个数据与输入有关,可以反映期望响应与实际输出之间的加权误差[5],其推导过程可由式2.2所得。
(2)正则化项
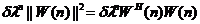 (2.8)
(2.8)
其中的δ是一个正常数,被定义为正则化参数[6]。除了因子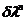 之外,正则化项的大小还取决于
之外,正则化项的大小还取决于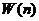 。代价函数中包含这项的作用是为了通过平滑作用来优化最小二乘的解。
。代价函数中包含这项的作用是为了通过平滑作用来优化最小二乘的解。
需要分析的是,指数加权因子λ的取值区间为(0,1],当λlt;1时,随着n的增大,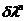 会逐渐趋于0,这也就表明着正则化项对于代价函数的影响会越来越小。式2.6是经常使用在RLS滤波器的设计。
会逐渐趋于0,这也就表明着正则化项对于代价函数的影响会越来越小。式2.6是经常使用在RLS滤波器的设计。
(3)正则方程的推导
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: