基于EMD分解和相空间重构的非线性信号特性分析方法研究毕业论文
2020-04-09 14:03:17
摘 要
信号有线性和非线性两种类型,而非线性信号分析是当前工程应用中亟待解决的难题,分析其混沌特性对于研究目标系统的状态具有重要意义。而相空间重构作为常用的非线性分析手段,受噪声等因素的影响较大,如何建立更加准确有效的相空间,是如今一个重要的科研课题。本文通过结合经验模态分解技术和相空间重构,采用经验模态分解算法对加噪后的Lorenz系统进行预处理,将有意义的成分从复杂的原始非线性信号中提取出来,再对Lorenz系统的时间序列进行相空间重构,接着研究了经验模态分解的分解效果以及噪声等因素对相空间重构的影响,并根据相空间重构方法提取延迟时间和嵌入维数,最后用小数据法计算出Lorenz系统时间序列的最大Lyapunov指数和关联维数,进而分析非线性时间序列的混沌特性。
关键词:非线性信号;经验模态分解;相空间重构;Lorenz系统;混沌特性
Abstract
There are two types of signals: linear and nonlinear. However, nonlinear signal analysis is a difficult problem to be solved in current engineering applications. Analyzing its chaotic characteristics is of great significance for studying the status of the target system. Phase space reconstruction, as a commonly used nonlinear analysis method, is greatly affected by noise and other factors. How to establish a more accurate and effective phase space is an important research topic today. In this paper, by combining the empirical mode decomposition technique and phase space reconstruction, the noiseless Lorenz system is preprocessed by using the empirical mode decomposition algorithm, and the meaningful components are extracted from the complex original nonlinear signals, and then Lorenz. The time series of the system is reconstructed in the phase space. Then the decomposition effect of the empirical mode decomposition and the influence of noise and other factors on the phase space reconstruction are studied. The phase space reconstruction method is used to extract the delay time and the embedding dimension. The data method calculates the maximum Lyapunov exponent and associated dimension of the Lorenz time series, and then analyzes the chaotic characteristics of the nonlinear time series.
Key words: nonlinear signal; empirical mode decomposition; phase space reconstruction; Lorenz system; chaotic characteristics
目 录
第1章 绪论 1
1.1 课题的研究背景及其意义 1
1.2 课题研究现状 2
1.2.1 EMD分解方法的研究现状 2
1.2.2 相空间重构理论的研究现状 2
1.3 本文的主要研究内容及组织结构 3
第2章 基于EMD算法的信号去噪分析 4
2.1 经验模态分解原理 4
2.1.1 EMD算法的基本概念 4
2.1.2 EMD算法的基本原理 5
2.2 EMD在信号降噪的应用 8
2.2.1 传统的信号降噪方法 8
2.2.2 EMD降噪方法 8
2.3 本章小结 10
第3章 混沌理论与相空间重构技术 11
3.1 混沌理论概述 11
3.1.1 混沌理论基本概念 11
3.1.2 最大Lyapunov指数 11
3.1.3 关联维数 12
3.2 相空间重构基本理论 14
3.2.1 延迟时间τ的确定 15
3.2.2 嵌入维数m的确定 17
3.3 基于C-C算法的延迟时间与嵌入维数计算 18
3.4 本章小结 19
第4章 非线性时间序列的相空间重构与混沌特性分析 21
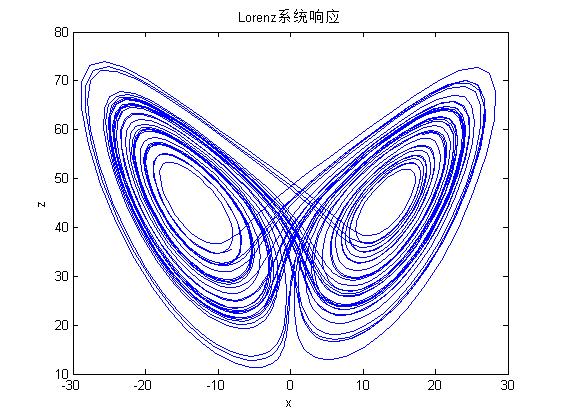
4.1 非线性序列的产生及Lorenz系统介绍 21
4.2 噪声对Lorenz序列混沌特性的影响研究 22
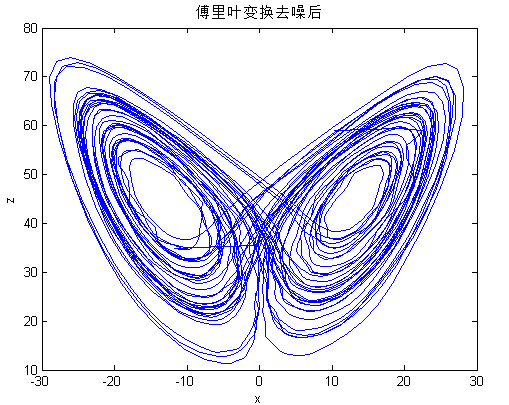
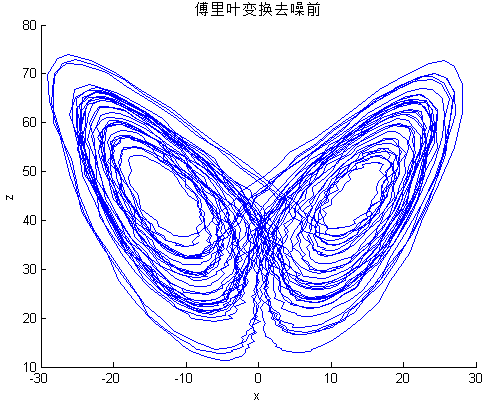
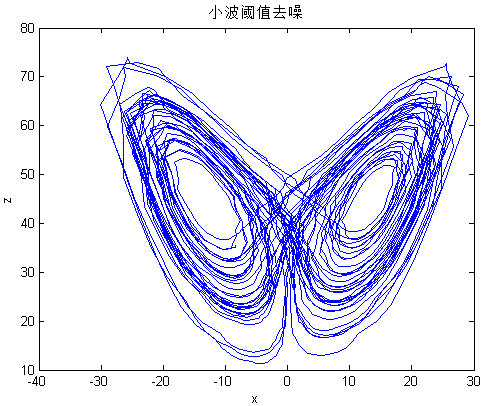
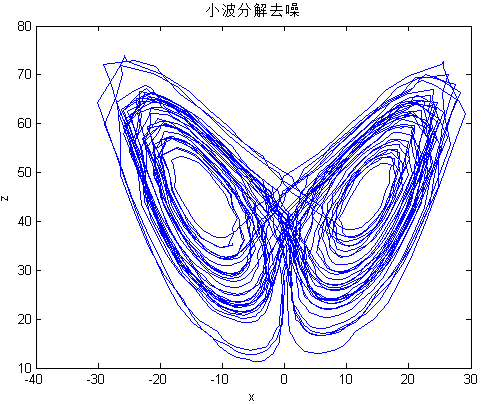
4.2.1 传统滤波方法对Lorenz序列降噪效果仿真对比 22
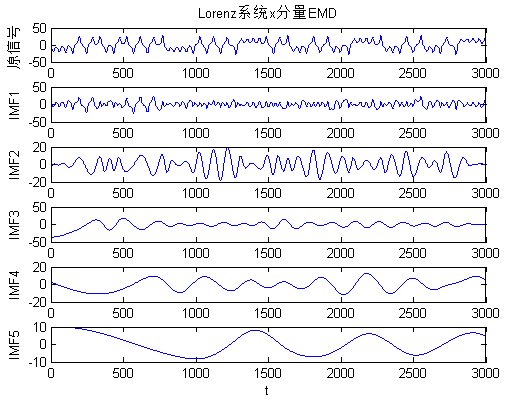
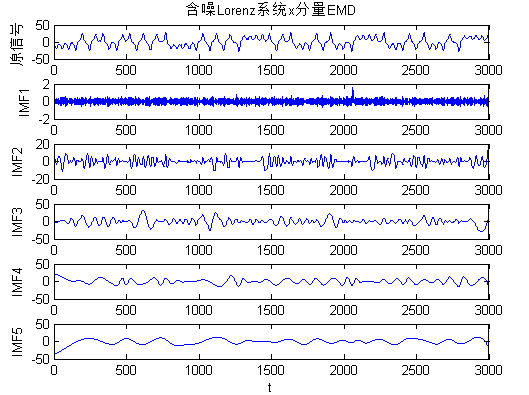
4.2.2 EMD方法对Lorenz序列降噪分析 23
4.3 基于EMD的Lorenz序列相空间重构 25
4.4 Lorenz信号的混沌特性分析 29
4.5 本章小结 31
第5章 总结与展望 32
参考文献 33
致谢 34
第1章 绪论
1.1 课题的研究背景及其意义
信号有线性和非线性两种类型,而非线性信号分析是当前工程应用中亟待解决的难题,分析其混沌特性对于研究目标系统的状态具有重意义。
经验模态分解(Empirical Mode Decomposition,EMD)方法是通过分析数据自身的时间长度来实现非线性信号的分解,不需要进行任何基函数的设置,此方法在该学术领域被称为是自以傅里叶变换为基础的线性和稳态频谱分析的里程碑,该方法的实现原理与采用先验性原理的谐波基函数和小波基函数上的傅里叶变换和小波变换存在根本区别[1]。
恰是因为如此的特色,EMD方法可以实现目前出现的所有信号,其在非平稳非线性的数据的处理过程中有其他方法无法比拟的优势,在处理分析非线性、非平稳信号序列时,相比其他方法具备更高的信噪比[2]。因此,EMD方法迅速在天气预测、水文预测、诊断机器故障等领域得到了广泛的应用,并取得了理想的效果[3]。
人们已经有很多方法来分析线性时间序列,但是使用这些方法分析非线性时间序列,往往没有得出所需要的效果。随着科技的进步,有人在研究过程中发现混沌现象也会发生在非线性时间序列,他们采用混沌原理对非时间序列进行探讨,这种方法后来被称为混沌时间序列分析法[4]。在分析系统的非线性动力学特征时,尽管它在时间上是一维的,首先就需要先恢复其所在的原高维动力学环境,相空间重构就是在这样的背景下应运而生。一般的时间序列和混沌时间序列分析方法不同,前者是在时间域中进行研究,而对于后者,是在所谓的相空间中进行混沌量的计算,混沌模型的建立和预测[5]。研究表明,在自然界和人类社会中处处充满了混沌现象,对混沌时间序列的分析也具有极其重要的价值。
对混沌时间序列的分析在很多领域得到了广泛的应用。在水文预测领域, Hense等人对每个月降雨量的间序列进行分析,开创性的提出了降雨量时间序列存在奇异吸引子的假设,并据此计算得到了其关联维数的取值区间。后来混沌理论在水文领域得到进一步的发展,Sangoyomi和Lall等人利用重构出来的相空间,描述和预测美国大盐湖的水量动力系统。在通讯领域,有人提出将通讯信号也假设成一种混沌时间序列,根据混沌理论对通讯信号的调制类型进行判断。在计算机技术领域,Erramilli等人用混沌理论对分组网的流量特征进行研究。Yangten等人利用混沌理论评估网络流量的性能,通过Lyapunov指数的取值区间来评估网络流量数据,很好的刻画出网络流量的增减情况,随着混沌理论的发展,在天文地理、经济科技等各个方面都能够建立基于混沌时间序列预测模型,并且取得了较好的预测效果[6]。
1.2 课题研究现状
1.2.1 EMD分解方法的研究现状
美国国家宇航局中的黄锷(N.E.Huang)等人在20世纪末提出了一种处理非线性非平稳信号的方法,能够自适应地处理信号时频,同时也拥有很高的信噪比,该方法后来被命名为经验模态分解法[7]。
经验模态分解法从根本上摆脱傅里叶变换理论的束缚,也克服小波变换的缺陷,无需预先设定任何基函数,通过数据自身的时间尺度特征对信号进行分解[8]。随着对EMD方法的深入研究,在工程领域应用极其广泛。如今国内外学者主要在工程应用研究和理论算法研究两大方面对EMD方法进行研究[9]。在工程应用研究方面主要包括水文预测、地理探测、地震预测、机械故障分析、血压波动和心律不齐分析等等[10]。在理论算法研究方面,开始是对EMD的包络拟合算法、IMF的筛选终止条件和EMD终止条件进行研究,而现在主要是对EMD自身的相关特征和EMD改进算法进行研究。
多年来, EMD算法不仅在理论方面获得重大突破,在应用方面也得到了迅速推广,但是EMD算法仍然没有严格的数学理论推导,在包络线拟合、模态混叠以及EMD终止准则等方面仍需要进一步解决[11]。
1.2.2 相空间重构理论的研究现状
时间序列分析简单来说就是对时间域内的数据进行研究,分析数据的规律,而分析混沌时序序列要以相空间理论来进行参数计算或者模型构建,因此在时序序列处理过程上相空间理论非常重要[12]。
Packard等人在1980年就已经给出导数重构和坐标延迟重构两种方法。但在相空间重构的过程中没有任何的先验信息,所以相空间重构一般采用坐标延迟方法。
1981年Takens提出嵌入定理:对于无限长和无噪声的d维混沌吸引子的一维标量时间序列,只要维数m≥2d 1,都可以在拓扑不变的意义下找到一个m维的嵌入相空间[13]。根据Takens嵌入定理,我们可以从一维混沌时间序列中重构一个与原动力系统在拓扑意义下一样的相空间,混沌时间序列的判定,分析和预测都是在这个重构的相空间中进行的,因此相空间的重构就是混沌时间序列研究的关键[14]。
1985年,时序序列的研究中的一个重大突破就是G-P坐标延迟算法的提出,坐标延迟的相空间理论关键便在于延迟时间以及嵌入维度的确定,Takens定理中说明的延迟数据为维度数据,在理论上可以取任意值,但是实际上对于一个有限长有噪音的信号,相空间重构的质量是由这两个参数的取值来决定的,因此如何选择合适的算法显得极其重要[15]。目前求取嵌入维数m和延迟时间τ的方法主要有两种,第一种方法假设m和τ是没有关联的,要想求取理想的嵌入维数必须先确定延迟时间。主要有自相关法,互信息法,复自相关法和平均位移法等方法可以用于求取延迟时间τ。主要有改进的Cao方法,虚假邻近法和几何不变法等方法确定嵌入维数。第二种方法确定这两个参数主要是通过计算嵌入窗宽来确定的,前提条件是延迟时间和嵌入维数是相互关联[16]。Kim等人于二十世纪末提出了C-C方法,是利用关联积分采用统计的方法确定出最佳时间延迟和嵌入窗宽,进而求出嵌入维数,这种方法尽管没有严格的理论基础支撑,但因所得结果比较理想,也被一些学者所采用。
1.3 本文的主要研究内容及组织结构
本文通过使用强大的Matlab工具软件,结合经验模态分解技术和相空间重构,在学习EMD算法和相空间重构原理的基础上,采用EMD算法对加噪后的Lorenz系统进行预处理,将有意义的成分从复杂的原始非线性信号中提取出来,再对Lorenz系统的时间序列进行相空间重构,接着研究了EMD的分解效果以及噪声等因素对相空间重构的影响,并根据相空间重构方法提取延迟时间和嵌入维数,最后用小数据法计算出Lorenz系统时间序列的最大Lyapunov指数,研究关联维数,进而分析非线性时间序列的混沌特性。
本文共分为五章,安排如下:
第1章 首先介绍了本课题的国内外研究背景和意义,以及目前国内外对EMD方法和相空间理论的研究现状。接着介绍本文的主要研究内容,最后对本文的组织结构进行阐述。
第2章 详细介绍了EMD算法,包括EMD算法的基本概念和基本原理,同时对比了传统滤波降噪的方法,提出了基于EMD的降噪方法。
第3章 首先介绍了混沌理论的基本概念、特征及其在非线性动力学方面的广泛应用。介绍了相空间重构的基本理论,采用坐标延迟法重构相空间需要计算相关的延迟时间和嵌入维数这两个参数,并且分别列举了它们的求取方法。
第4章 根据前两章的理论知识,首先对含噪的Lorenz系统进行EMD降噪处理,分析噪声对相空间重构的影响。随后,对Lorenz系统进行相空间重构,分析其混沌特性。
第5章 总结本文主要的内容,反思文中仍然存在的不足,指出以后能够深入研究的方向。
第2章 基于EMD算法的信号去噪分析
2.1 经验模态分解原理
2.1.1 EMD算法的基本概念
短时傅立叶变换(short-term Fourier transform,STFT)、小波分析等在时间域和频域分析方法的理论基础实质上就是通过傅里叶变换来进行实现的,找到信号频率随时间变化的规律是分析非平稳信号最重要的步骤,但是用傅里叶变换分析处理非平稳信号时并不能得到想要的效果。N.E.Huang等人就是在当时的时代背景下创造出了用经验模态分解方法获取本征模态函数(Intrinsic Mode Function,IMF)的理论思想,同时又进一步研究了希尔伯特黄变换(Hilbert—Huang Transform,HHT)的适用范围。经验模态分解方法的核心是获取瞬时频率,用经验模态分析法分析可以很容易并且很准确的得到不同频率下随时间变换的信号分量,而这点通过傅里叶变换肯定是不能完成的。本章将重点阐述瞬时频率以及本征模态函数等概念,并分析EMD算法的基本原理,研究EMD算法流程等内容。
EMD算法主要是求解瞬时频率、求解特征时间尺度和得到本征模态函数。在对EMD进行时间域和频域的分析过程中,主要有如下两个步骤:
(1)通过对时间序列进行经验模态分解,来得到一组本征模态函数;
(2)对上一步分解得到的这组本征模态函数进行HHT变换得到时频谱图,再进行分析。
传统的时频分析方法不再适用于对非平稳非线性信号的分析,因为其过程复杂,频率也变化剧烈,在此处需要引入与传统意义上不同的瞬时频率来进行分析,能够更加精准的分析出非线性非平稳信号的局部特征。传统频率的计算公式如下:
(2.1)
在N.E.Huang等人提出的Hilbert变换之前,瞬时频率没有统一的定义,N.E.Huang等人对于连续时间信号x(t)的Hilbert变换Y(t)定义如下:
(2.2)
将Hilbert变换Y(t)与x(t)复共轭对得到解析函数Z(t):
(2.3)
其中,为瞬时幅度,为瞬时相位。
瞬时频率S(t):
(2.4)
由式(2.4)可得,瞬时频率是信号对时间求解微分的结果,其频率值在任意时刻是唯一确定的。
本征模函数的概念源自于物理学中的瞬时频率,对于某个由瞬时频率的函数,它的零极点和均值在坐标轴上都有一定的对称性和特征性。同时,该函数所描述的某种信号都可以由一个或多个本征模函数来表示。根据本征模函数的多个频率点的特性,可以将多个函数进行叠加等运算,得到一个新的信号。利用上述对频率函数拆分叠加的原理,可以知道EMD算法的实质就是把信号的本征模函数分离出来,然后再进行希尔伯特变换以得到相应的频谱。
本征模函数具有两大特点,一是频谱图在时间轴上有相同数量的零极点,这就使得它与一般的窄带高斯信号的频谱特性相比几乎是相同的;二是在时间轴上任意一点处图像包络的上下两部分的平均值相等,即可以相互抵消。根据它的第二个特点,一个本征模函数就可以完全从其局部包络来反映,而函数图像整体上的不对称性不会影响到某个点或局部的特性,只要满足包络局部均值为零即可。所以本征模函数的第二个特点,也可以表述为利用函数图像包络的局部均值为零来等效于该函数所表示信号的局部对称性,这种等效替代的方法在研究中也被证明是可行的。由于本征模函数所表征的是某种信号物理学上的运动特性,其图像在每两个过时间轴交点之间的部分定义为一个振动周期,每个周期对应一种振动模式,并且本征模函数可以表述不同类型的调制信号,可以是稳态或者非稳态的或者是窄带或非窄带信号,也可以是频率或幅度的调制信号。
综上所述,我们可以看出EMD算法就是从信号中分离提取本征模函数的过程,这个过程就是先分析信号频谱在时间轴上的特性并对其进行相应的计算,再对所得的数据分解。对数据的处理方式实质上是根据不同类型的时间间隔来区分信号的波动方式,主要有两类:第一类是按照频谱函数在时间轴上相邻零点之间的间隔来区分;第二类是按照波形包络的顶点和谷点所对应的时间点之间的间隔来区分的。在实际算法应用中,我们常采用第二类区分原理,以获取更高的频率分辨率。
2.1.2 EMD算法的基本原理
对给定信号x(t)的EMD分解算法具体流程如下:
(1)计算x(t)在时域上的全部的局部极值点,采用三次样条插值法,拟合上包络线u(t)和下包络线d(t),通过上下包络求取均值,再用原始信号减去得到,公式如下:
(2.5)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: