摘 要

船舶与海洋工程水动力学中涉及大振幅晃荡、甲板上浪、波浪爬升、气隙、砰击等极其复杂的“多相”、“多体”、“多尺度”、“多自由度”、“多模型”非线性流固耦合响应，包含众多的大变形、高度湍流涡团、飞溅及碎波等物理现象，是高度非定常、强非线性的动力学问题，理论分析和数值求解异常复杂。随着计算流体动力学（CFD）前沿技术的发展，目前广泛采用CFD技术高效准确模拟船舶与海洋工程水动力学所面临的强非线性问题。就CFD方法而言，CFD前处理如几何建模和面网格生成质量，将直接影响CFD计算的精度，是流场数值模拟的基础，也是目前CFD前处理研究的热点。

本论文的主要内容是，追踪与收集国内外基于隐式曲面技术建模的发展动态，学习与应用本论文提出的基于笛卡尔背景网格的径向基函数隐式曲面构造技术，选择典型的曲面几何建模算例，测试现有的程序，验证该方法的精度与有效性。

关键词：隐式曲面；径向基函数；几何建模；面网格生成

Abstrct

The hydrodynamics of ships and marine engineering involves extremely complex “multi-phase”, “multi-body”, “multi-scale”, “multi-degrees of freedom” such as large amplitude sloshing, wave on the deck, wave climbing, air gap, and slamming. The "multi-model" nonlinear fluid-solid coupling response includes numerous large-deformation, highly turbulent eddies, splashes, and shatter waves. It is a highly non-stationary and strongly nonlinear dynamic problem. Theoretical analysis and numerical solution are extremely complex. . With the development of computational fluid dynamics (CFD) cutting-edge technology, CFD technology is now widely used to efficiently and accurately simulate the strong nonlinear problems faced by hydrodynamics of ships and marine engineering. As far as the CFD method is concerned, CFD pre-processing such as geometric modeling and surface mesh generation quality will directly affect the accuracy of CFD calculations. It is the basis for numerical simulation of flow fields and is also a hot topic in current CFD pre-processing studies.

The main content of this paper is to track and collect the development of modeling based on implicit surface technology both at home and abroad, and to study and apply the radial basis function implicit surface construction technology based on Cartesian background mesh proposed by the research team of this topic. A typical surface geometry modeling example tests existing programs to verify the accuracy and effectiveness of the method.

Key words:implicit surfaces; radial basis functions; geometric modeling; surface mesh generation

目 录

第1章 绪论 1

1.1 研究背景及意义 1

1.2 研究内容 2

1.3 本文的研究目标及意义 3

第2章 曲面几何建模方法 5

2.1 显式曲面几何建模 5

2.2.1 参数曲面 5

2.2.2 网格曲面 6

第3章 隐式曲面几何建模 7

3.1 隐式曲面几何建模 7

3.2 径向基函数概述 7

3.3径向基函数隐式等值面构造 9

第4章 基于径向基函数插值方法的数值算例及结果分析 12

4.1基于全局支撑径向基函数的数学模型 12

4.2 一种基于全局支撑径向基函数的隐式等值面构造方法 13

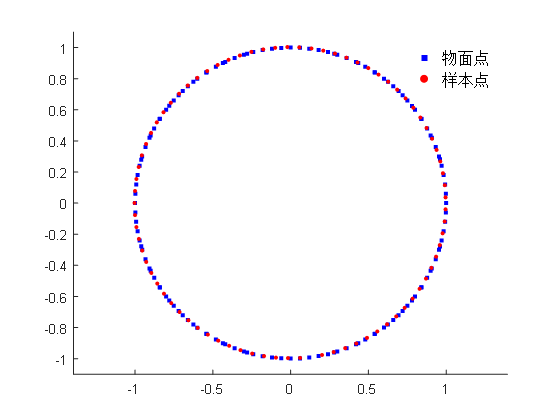
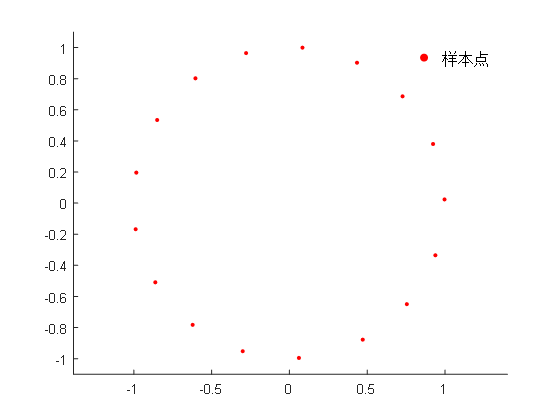
4.3二维几何剖面重构 15

4.4 三维复杂几何曲面重构 20

第5章 总结与展望 23

参考文献 24

致谢 25

第1章 绪论

1.1 研究背景及意义

船舶与海洋工程水动力学中涉及大振幅晃荡、甲板上浪、波浪爬升、气隙、砰击等极其复杂的“多相”、“多体”、“多尺度”、“多自由度”、“多模型”非线性流固耦合响应，包含众多的大变形、高度湍流涡团、飞溅及碎波等物理现象，是高度非定常、强非线性的动力学问题，理论分析和数值求解异常复杂。随着计算流体动力学（CFD）前沿技术的发展，目前广泛采用CFD技术高效准确模拟船舶与海洋工程水动力学所面临的强非线性问题。就CFD方法而言，CFD前处理如几何建模和面网格生成质量，将直接影响CFD计算的精度，是流场数值模拟的基础，也是目前CFD前处理研究的热点。

在强耦合分区方法理论的框架下，粘性水弹性理论的数值方法大致分为两类：边界拟合法和非边界拟合法。其中，边界拟合法如传统的任意拉格朗日−欧拉法（ALE，Arbitrary Lagrange Euler Method）^[1]，贴体网格生成依赖于浸入结构体的几何形状（见图1-1为球鼻贴体结构网格图），多数采用显式曲面建模模型，比如，经典的NURBS曲面，通过建立物理域到参数域的变换来构建几何曲面，确保曲面上给定点坐标的计算精度，容易实现曲面的真实形状。非边界拟合法如传统的浸入边界法（IBM，Immersed Boundary Method），笛卡尔背景网格与浸入结构网格各自独立，多数采用隐式曲面建模模型，比如，径向基函数（RBF，Radial Basis Function）建模方法，用于描述任意复杂的几何外形（见图1-1笛卡尔背景网格中浸入球鼻结构网格图），快速识别场点相属性（即空间场点与曲面的相对位置），是非边界拟合法的核心技术之一。径向基函数是一类以欧式距离为变量的基函数集合，具有概念简单、实施方便且适用于含复杂拓扑结构几何建模问题。

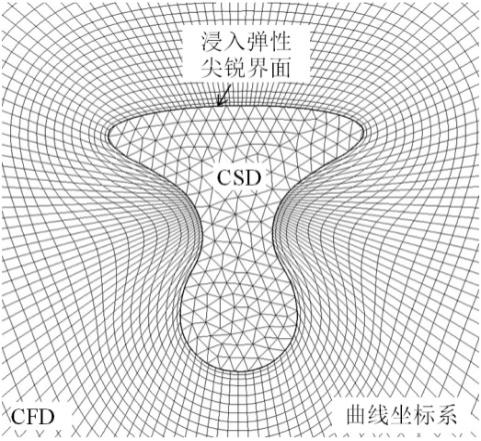
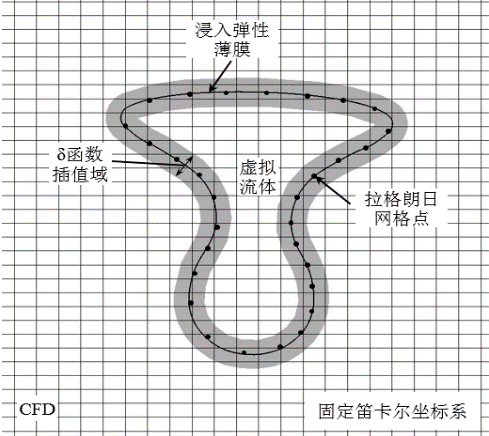
图 1-1 边界拟合法（左边）与非边界拟合法（右边）结构网格示意图

1.2 研究内容

显式曲面建模中着重于直接从曲面边界形态入手，通过基函数拟合或者离散的方法逼近曲面几何边界。比如，常用方法有Bezier曲面构造、B-Spline曲面构造、NURBS（Non Uniform Rational Basis Spline）曲面构造等方法。与之相对，隐式曲面几何构造不直接针对边界形态建模，可以看作引入场的概念，在一个标量场中提取曲线/面信息（如特定等值线/面）。这类方法极大的提升了表达复杂曲面的灵活性和自由度。隐式曲面建模技术，自80年代初Blinn^[2]和Nishimura l^[3]分别提出元球模型以来，隐式曲面方法在计算机动画等领域得到了广泛的重视（见图1-2）。

径向基函数方法是隐式曲面建模技术研究中最多的方法之一，也是一种有效的逼近理论，具有原理简便、易于编制计算程序和计算精度高等特点，尤其在求解偏微分方程中，避免采用计算数值积分^[4]。

基于径向基函数边界插值算法的研究，首先来自Alrem等应用径向基函数方法应用于研究跨音流动中飞机的静变形。其次，主要集中于解决气动力学非线性大变形流固耦合问题（如CFD网格形式多为动网格），插值的对象为气动网格位移。目前，在船舶与海洋工程水动力学研究领域，不同网格下的边界数据传递则通常采用商业软件自带多场求解器，如ANSYS的MFS和MFX求解器，或者是利用专门多物理场耦合软件。针对基于笛卡尔背景网格的隐式曲面建模方法研究的文献更是鲜见。

径向基函数方法具有显著的特征，比如，适合于散乱数据问题，不局限于网格数据；插值精度高，具有较高的指数级收敛；若径向基函数矩阵为正定，其线性组合可逼近任何连续函数；适合低维、多维空间。近年来，广泛应用于各个领域，如偏微分方程的求解，热传递，固体振动，板壳理论，固液相变，三维形貌重建，等等。

目前径向基函数方法研究可概括为两大类：全域径向基函数插值方法和紧支域径向基函数插值方法。Krige于1951年首次提出基于Kriging方法的径向基函数技术。径向基函数理论及方法自提出之日起，受到了广泛关注，不断得到丰富和发展，应用也日趋广泛。比如，应用于曲面拟合的Multi-Quadric方法，以及研究Multi-Quadric插值矩阵的逆矩阵。然而，基于径向基函数的隐式曲面建模方法，仍有一定的局限性，比如若处理大规模、大尺度计算问题，由于数据节点庞大，每一时间步需求解大型满秩矩阵，使计算量显著增加。为此，针对该问题，求解策略是采用分区径向基函数方法。

针对船舶与海洋工程隐式曲面建模问题，本论文的主要内容分为以下三部分：

（1）追踪与收集国内外基于径向基函数的隐式曲面建模技术的发展动态；

（2）学习现有程序的主程序结构；

（3）选择合适的算例，测试现有的程序，进行二维、三维几何建模及面网格生成。

移动最小二乘法

局部方法

优点：可快速地对大数据集进行曲面构造，能准确地构造曲面的尖锐特征 。

不足：难以处理有较大空洞区域的模型，不能有效地处理噪声。

。

B样条曲面；

NUBRS曲面

MPU方法

隐式曲面构造方法

优点：对于任意复杂几何模型，能以较少的离散点构造出光滑曲面；算法简单易实现，且具有较高的精度。

不足：若模型不够光顺或者几何连续性差，会出现局部失真，难以构造出曲面的尖锐特征。大数据集计算效率较低。

径向基函数方法

全局方法

优点：可构造非常光滑的曲面，对噪声不敏感；求解问题可简化为稀疏线性系统，提高计算效率。

不足：容易将不该连接的点云空洞连接起来。

泊松方程法

图 1-2 隐式曲面建模方法

1.3 本文的研究目标及意义

本论文研究目标及意义在于，学习与应用本论文提出的基于笛卡尔背景网格的径向基函数隐式曲面构造技术，应用该程序，对典型的二维、三维几何建模及面网格生成，验证该方法的精度与有效性。

本文首先概述曲面几何建模方法，其次，介绍经典的浸入边界法，最后阐述基于笛卡尔背景网格的径向基函数隐式曲面构造技术及其数值算例。

第2章 曲面几何建模方法

求解含复杂外形，强耦合的非线性水动力响应问题的两类主要数值方法（贴体网格方法和非贴体网格方法，其中非贴体网格法又分为扩散界面法及锐利界面法），分别对应几何建模方法（显式曲面几何建模、隐式曲面几何建模）。本文的主要目的是针对锐利界面方法中曲面建模方法进行优化。为此，下文将介绍几何建模中的显式以及隐式建模方法的发展和现状。

2.1 显式曲面几何建模

显式曲面构造中，曲面几何边界由组合的多个基函数或者离散线/面表征，非常直观易于理解，适用于贴体网格构建。显式曲面构造方法又可细分为参数曲面构造和网格曲面构造。

其中，参数曲面方法主要通过控制点坐标，组合相对应的（加权）基函数明确表征曲线/面。常用方法有Bezier曲面构造、B-Spline曲面构造、NURBS（Non Uniform Rational Basis Spline）曲面构造等方法。其中Bezier曲面构造法和B-Spline曲面构造法都是通过控制点和相应基函数组合形成相应曲面。这两类方法的区别在于，Bezier曲面构造中任何一个控制点可全局影响曲线/面形态；而在B-Spline曲面构造中，调整任何一个控制点仅影响当地曲线形态。由此可见，Bezier曲面构造更为简单易行，但是难于精确调整曲线/面局部特征。与之相对，B-Spline方法更利于调整曲线/面局部特征，构建较为复杂的曲线/面。另外，NURBS曲面构造方法的特点在于曲线/面控制点可为不均匀分布，并且各个控制点均可调整。在构造曲面时，NURBS方法首先通过构造二维曲线，曲线的空间组合构造曲面。这些特性让NURBS在构造复杂几何曲线/面时有更大的自由度，并且能更好的在实际应用中生成复杂几何外形。

另外一种显式曲面构造方法为离散网格曲面构造。这类方法的主要途径为离散曲面，使用线段或者网格单元面逼近光滑曲线/面。在构造曲面过程中，三角形和四边形网格为最为常用的网格单元。其中四边形网格更为规则，而三角形网格组合更为灵活、更易于应用于复杂外形的几何逼近。

下面，以参数曲面与网格曲面为例，简单说明。

2.2.1 参数曲面

参数曲面将点坐标表示成与特定参数相关的函数，作为变量的参数通常被限制在一定的范围内，称之为定义域，可选取不同的参数来表达物体曲面。参数曲面能将构造曲面的三维问题转化为对应参数域的二维问题。参数曲面是描述物体的几何形状和拓扑结构的常用工具，在计算机图形学中得到广泛地应用。

参数曲面的参数方程在不同坐标系中有相同的形式，对参数曲面进行几何变换也很方便，其形状易控制，物体位置移动可直接通过坐标变换实现。参数曲面适合处理多值问题，便于描述曲线的分段和分片^[5]，且容易通过人机交互编程实现。参数曲面表示方法虽然简单易行，但也存在诸多局限性。例如用参数曲面表示复杂曲面时，需要拼接多个简单曲面，通常难以保证其几何连续性，对于拓扑结构复杂、几何特征较丰富的曲面难以进行精确描述，对点、线、面的相对位置关系也难以准确判定，因此，参数曲面不适于用来表示复杂曲面。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：