摘 要

从室内试验和现场原位试验中得到的岩土数据具有很强的离散性，提高样本数量是降低离散性的途径之一，但由于工程预算等因素的限制，试样数量不可能大规模提高。为解决该问题，通过室内试验获取一组红砂岩单轴抗压强度数据，以不同的样本数量从中遍历取值，研究试验数据的离散性随样本数量的变化特征。研究发现样本均值的变异系数与试样个数呈负相关关系，当样本均值的变异系数在0.05以下时，岩样数目至少为6个。用概率分析方法分析估计具有不确定性的岩石参数是一种有效方法，本文通过这一组红纱岩单轴抗压强度数据，对比t分布方法、Bootstrap方法和Bayes方法，分析其优缺点，为红砂岩相关工程中的单轴抗压强度统计估计提供参考。

关键词：小样本；单轴抗压强度；离散性；统计分析方法；红砂岩

Abstract

The geotechnical data obtained from laboratory test and field in-situ test have strong discretization. Improving the number of samples is one of the ways to reduce the discretization. Due to the limitation of engineering budget and other factors, the number of samples cannot be increased on a large scale. In order to solve this problem, a set of uniaxial compressive strength data of red sandstone was obtained through laboratory tests, and the values were traversal with different sample Numbers. The dispersion of test data with the number of samples is studied. It showed that the variation coefficient of the mean of samples was negatively correlated with the number of samples. When the variation coefficient of the sample mean is below 0.05, the number of rock samples is at least 6. Probability analysis is an effective method to estimate the uncertain rock parameters. This paper compared the t-distribution method, Bootstrap method and Bayes method with the uniaxial compressive strength data of this group of red sandstone, and analyzed their advantages and disadvantages, which can provide a reference for the statistical estimation of uniaxial compressive strength in red-sandstone related projects.

Key Words：small sample；uniaxial compressive strength；discretization；statistical analysis method；red sandstone

目 录

第1章 绪论 1

1.1 选题背景及其研究意义 1

1.2 国内外研究现状 1

1.3 研究目的及研究方法 4

第2章 红砂岩单轴抗压强度试验 5

2.1 红砂岩单轴抗压强度试验方法步骤 5

2.2 红砂岩单轴抗压强度试验结果 6

第3章 小样本均值及离散性分析 8

3.1 抽样实验 8

3.1.1 将30个单轴抗压强度值视为总体样本 8

3.1.2 组合抽样 8

3.1.3 实验分析 12

3.2 小样本均值的离散性分析 13

3.3 小结 14

第4章 常用的参数统计分析方法 15

4.1 均值法 15

4.2 区间估计法 16

4.2.1 t分布法 16

4.2.2 均值估计 16

4.3 Bayes方法 17

4.3.1 Bayes公式 17

4.3.2均值估计 18

4.4 Bootstrap方法 20

4.4.1 Bootstrap方法步骤 20

4.4.2 均值估计 20

4.5 小结 23

第5章 结论 24

参考文献 25

致谢 27

附录 28

附录A 28

附录B 28

第1章 绪论

1.1 选题背景及其研究意义

红砂岩是一种沉积岩，大约产生于中生代白垩纪时期^[1]，由于含有丰富的氧化物，一般呈现为红色、深红色或者褐色，主要有粒状碎屑结构以及泥状胶结结构两种典型的结构形式。红砂岩一般按照单轴抗压强度和崩解特性进行分类，一类二类红砂岩容易崩解破碎，强度较低；三类红砂岩基本不崩解，其天然单轴抗压强度大于15MPa。红砂岩在我国和全球都分布较广，我国的红砂岩约有82.6万km²，大约占陆地总面积的8.61%^[2]，主要分布在四川、云南、湖北、湖南、江西、甘肃、山东、青海、安徽等地区^[3]。由于经历漫长的地质年代、沉积和人类活动，红砂岩的性状同其他岩石一般具有不确定性。随着我国岩土行业的深入发展和建设项目显著增多，工程中常常会遇到这类岩体，确定红砂岩的单轴抗压强度等物理力学特性是工程建设和研究的需要。

单轴抗压强度是岩石质量分级和岩性描述的重要指标^[4]，岩土工程中常需测得岩石的单轴抗压强度来为工程勘察、结构设计与检测评估提供相关力学参数。红砂岩的单轴抗压强度受其微结构参数与基本物理指标影响很大^[5]。岩石作为一种天然的非均质各向异性体，其本身具有很大的离散性，小样本情况下所测得的单轴抗压强度与真实强度之间存在一定误差。红砂岩由于受地理位置、风化程度等沉积环境影响，其矿物成分、微结构特征、胶结程度等在形成和赋存过程中便具有较大差异，使得其物理力学参数值变化较大^[5,6]，即红砂岩的固有变异性较大。冷伍明等认为不确定性大致分成两种，固有变异性和系统不确定性，前者是客观存在的且一般无法避免，后者又包括模型不确定性、试验不确定性以及统计不确定性^[7]，其中统计不确定性大部分是样本不够充足导致的。若要统计估计得到一个较精确的值，需要详尽的信息，即充分的样本数目。由于工程预算、取样困难、时间因素等限制，很多时候试样数量不能大规模提高，这会导致信息的不完备和参数估计的不确定性，定量分析岩样数目对单轴抗压强度离散性的影响、找出小样本情况下红砂岩单轴抗压强度的统计特征和取值方法，将为可靠度研究和工程应用提供一定参考。

1.2 国内外研究现状

在实际工程中，为获得岩石单轴抗压强度，最简单常规的方法是取几个岩石样本进行室内试验或现场试验，再求这几个岩样的平均值作为该岩石单轴抗压强度。国际岩石力学学会建议至少应取6个岩石样本试验后取平均值作为岩石单轴抗压强度^[8]，我国规范规定单轴压缩试验至少取3个岩石样本^[9]，工程试验中则至少取6个岩石样本^[10]。试验之后的工程设计或验算中有时会考虑将几个样本的平均值进行折减和修正，多数情况是乘以规定的安全系数。岩石的类型和试验方法如果不同，那么它们的特征参数也将千差万别，所需的最小岩样数目也不相同^[11]。对于大样本和小样本目前没有明确的数目划分，大部分学者认为样本数目取30是二者的分界值，王少红认为样本容量10以上的可以称作大样本^[12]。在保证岩石参数一定可靠度的情况下，人们都希望采用尽可能少的岩石样本来降低人力成本、时间成本和经济成本。找出岩石试验的最佳样本数量是国内外学者研究的方向之一。吴振君等提出一种在总体中多次随机抽样来模拟真实取样的分析方法，在假定参数变异性已知的条件下对边坡可靠度结果进行分析，认为不排水强度参数的变异系数在0.2～0.5范围内，则边坡样本数目应取10～15 ^[13]。赵晶等在参数总体分布中进行120次重复的随机抽样，从而构建样本统计值空间，分析数据离散性，在可靠度指标的变异系数为0.3的条件下推算所需样本数目，建议参数呈大、中、小三个不同的变异水平时，样本数目分别取18、11、6^[14]。秦善勇等给出了抽样数目和可靠度指标相对误差之间的关系曲线及其拟合公式，并认为在大样本数据中随机抽取小样本进行分析时，小样本数目应比总体样本数目的20%更多^[15]。

岩石力学及相关工程在萌芽时期由于知识水平局限等问题，几乎都是依赖过去的经验解决问题；20世纪开始出现了各种经典理论，岩土工程蓬勃发展，在这期间发展了许多定值分析方法，即确定性研究方法，直到现在这些方法仍然应用广泛，然而在这些模型中，很多不确定的影响因素都被忽略掉了；20世纪60年代开始，岩土工程进入了现代发展阶段，岩体被认为是系统概念，被认为是复杂的、多变的，70年代我国开始了岩土工程可靠度研究，80年代末有学者提出了不确定性研究理论^[16]，众多研究人员也都意识到不确定性研究的意义与必要性，岩土工程逐步进入概率分析方法与可靠度研究阶段，不确定性理论体系逐渐建立和发展。

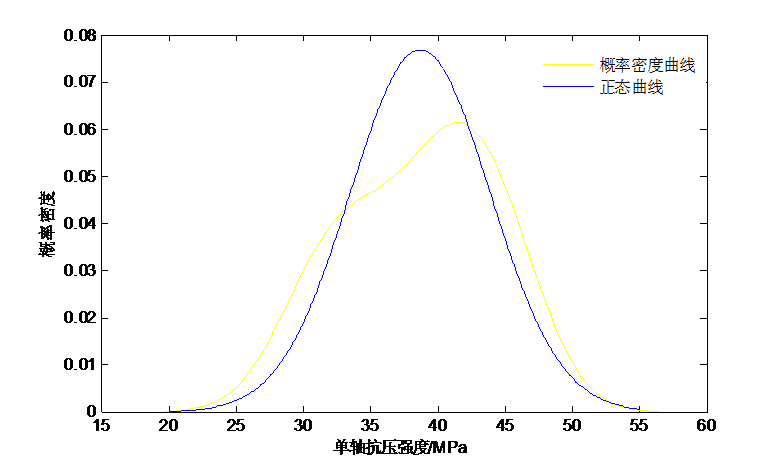
岩石的实际物理力学参数的真值是难以确定的，而研究和工程需要对具有很大离散性的岩体力学参数进行数学意义上的定量化描述，这时一般将其视作具备概率分布特征的连续型随机变量，通过随机变量的分布形式和均值、方差等特征参数来描述岩土参数，而岩石自身的不均匀性、取样及试验的系统误差和工程样本数目的限制使得岩土参数的概率分布形式很多时候表现出很大不确定性^[17]。一般认为，大量的岩石单轴抗压强度值服从正态分布。在已知或假设出总体分布的情况下，国内外专家学者提出了Bayes方法等参数概率统计分析方法，在未知总体分布的情况下，国内外专家学者提出了Bootstrap法等参数概率统计分析方法。

区间分析法是一种在各行各业都应用较广的统计分析法。董陇军等提出了岩石抗拉区间强度与抗压区间强度的相关概念和求解方法，认为用区间强度来代表岩石强度相较于传统均值代表岩石强度时的保证率更高，表达的岩石强度信息也更加充分完善^[18]。王浩等进行岩石单轴抗压强度试验后用置信区间分析结果，对比认为该方法所得的单轴抗压强度较平均值法所得值更靠近真实值^[19]。根据概率学与数学知识，对于总体呈正态分布的小样本数据，t分布是其最匹配的概率密度拟合，当样本数量足够多，即n足够大时，t分布将近似于正态分布。岩土工程中，一般按单侧取95%的置信概率，即将均值小于置信下限的风险控制在5%以内。窦文俊等采用t分布法,对东海大桥的陆上段桥梁各墩沉桩施工和静力触探的小样本Ps标准值进行了一系列统计和分析^[20]。

1979年Efron最早提出了Bootstrap（自助）方法^[21]，将小样本问题转化成大样本问题。2009年谢桂华首次将Bootstrap方法引入了岩土力学参数的统计分析，通过计算机抽样模拟解决了小样本情况下参数分布的推断问题，并且该方法无需假定岩体参数的分布概型，适用性较为广泛^[22]。骆飞等认为在同一置信水平下，Bootstrap方法可以充分利用小样本的经验分布信息，能够将c、φ均值的置信区间进行有效地收窄，使其下限值相对传统的t分布方法而言，更为接近真值，误差更小^[23]。唐小松等提出了一种基于Bootstrap的最优边缘分布函数和最优Copula函数的识别方法，并用桩基的荷载-位移曲线数据作为示例证明该方法的有效性，为Bootstrap法提供了一种新的思路^[24]。李麟玮等在四种常用的Bootstrap法与KELM-BPNN模型的基础上，提出了一种新的滑坡位移区间预测模型，使滑坡灾害预警有了新的有效途径^[25]。张隆松等提出了一种将Bootstrap法和概率密度加权法相结合的基坑变形可靠度分析法，并对台北TNEC基坑工程变形的可靠度进行分析，证明该方法能合理考虑统计不确定性、高效计算可靠度^[26]。

近年来，工程中经常以Bayes估计方法来获取小样本参数特征，该方法的最大特点是需要积累大量的的先验信息，即验前信息，认为参数有验前概率密度，然后结合试验所获取的新信息，来推测小样本岩石参数的后验分布和特征参数。光耀华给出了计算机上岩土工程参数的统计过程和Bayes取值方法^[27]，为Bayes方法的应用奠定了一定基础。徐军等将Bayes方法和模糊数学理论结合，给出一种模糊Bayes方法来确定小样本岩体参数的概率分布,并强调先验信息的重要性^[28]。毕中伟等讨论了Bayes方法中前验信息的获取、分类以及可信度检验，并用Bayes方法对康家湾的铅锌金矿的土工参数推断计算，建立了该金矿围岩的计算模型^[29,30]。严春风等在Bayes最小熵原理以及优度比较检验的基础上建立了一个统计推断体系，该方法可以在岩样数目较少导致无法单独拟合概率分布函数时，推断不同概率模型的概率分布函数，并且能通过比较检验来确定最优函数^[31]。闫春玲通过参考其他Bayes理论公式给出了岩石抗压强度中的Bayes均值和方差估计公式^[32]。

除去均值法、区间估计法、Bootstrap法和Bayes法这四种应用较多的方法，许多专家学者也提出了一些其他应用于小样本可靠度或概率分布特性研究的相关方法。孙慧玲等运用蒙特卡罗仿真法进行仿真，对比分析了经典统计法、Bootstrap法与Bayes Bootstrap法，认为样本量极少的时候，Bayes Bootstrap法比较适用^[33]。申翃建议对土工试验数据采用Grubbs法进行可靠性方面的检验^[34]。贡金鑫等基于线性最小偏差的参数估计方法对所估计参数的概率特性进行了分析，认为岩土工程中极小样本的统计分析适合用线性最小偏差法^[35]。邓建等以信息论的最大熵原理为基础，通过牛顿迭代法，根据样本矩推断了小样本岩石参数的概率密度函数，并用K-S检验法进行检验^[36]。苏永华等对岩土参数大子样条件下的多项逼近法拟合概率密度函数的优缺点进行了讨论^[37]。

总的来说，目前已有众多岩土参数概率统计方法。对于工程中红砂岩单轴抗压强度的取值，应视不同情况和要求来选定最佳方法。本文以一组云南某地红砂岩单轴抗压强度为例，研究均值法中样本个数与离散性的关系，探讨t分布方法、Bootstrap方法和Bayes方法的取值效果。

1.3 研究目的及研究方法

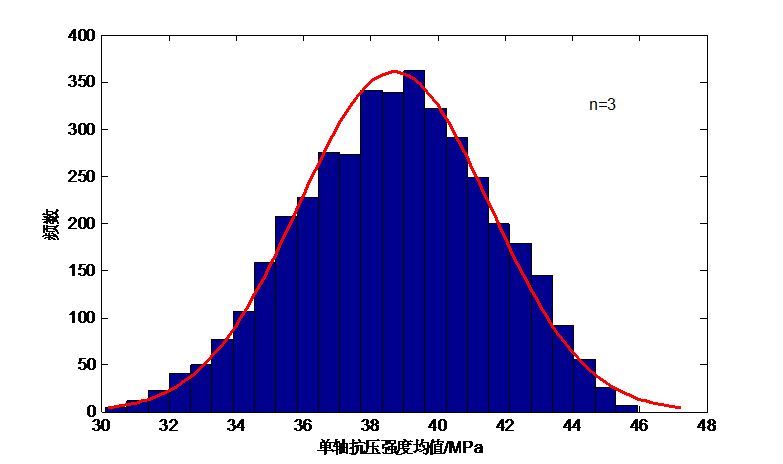
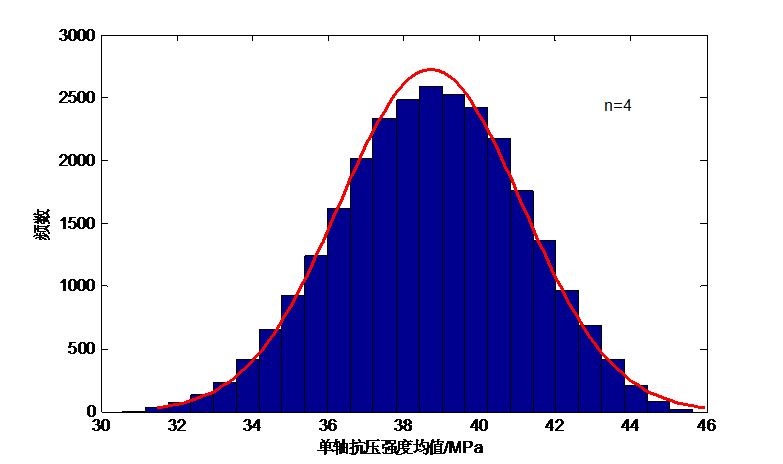
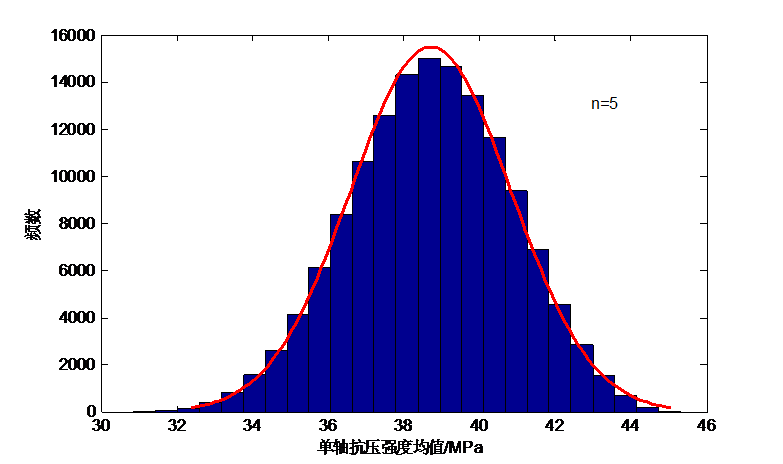
红砂岩的单轴抗压强度具备很大的离散性，试验岩体样本数目不充足是导致其不确定性的原因之一。本文拟参照《工程岩体试验方法标准》，完成30个标准圆柱红砂岩试样的单轴抗压强度室内试验，以这30个单轴抗压强度值代替总体，借鉴数学中抽样组合的思想，从中任意抽取不同样本容量的小样本，用MATLAB分析抽样后的所有小样本均值的频数特征与变异系数，找出最佳样本容量数目。

近年来岩土工程中常以概率统计方法分析岩体参数，本文列举出较为通用的区间估计法、Bootstrap方法和Bayes方法的中心思想，并基于上述红砂岩单轴抗压强度试验数据，讨论分析各个方法的特点和优缺点，找出红砂岩单轴抗压强度测定时的最佳小样本统计分析方法。

研究流程如图1.1。

图1.1 研究流程图

第2章 红砂岩单轴抗压强度试验

2.1 红砂岩单轴抗压强度试验方法步骤

选用产自云南某地的红砂岩，在室内进行单轴抗压强度试验。

（1）将红砂岩加工成30个φ50mm×100mm的标准的圆柱体试样（如图2.1、图2.2），试样表面无裂缝，试样两端平整。

图2.1 红砂岩试样1号 图2.2 红砂岩试样2号

（2）对红砂岩试样进行编号，依次测量出直径、高度，算出截面积。

（3）本次单轴试验在红砂岩自然状态下进行。

（4）将红砂岩试样置于RMT-150C岩石力学试验系统的承压板中心，调整位置使试件两端面接触均匀，以0.002mm/s的速度加载至破坏，得出最大峰值荷载。

（5）根据《工程岩体试验方法标准》规定，按照公式（2.1）得出每个红砂岩试样的单轴抗压强度^[9]。

（2.1）

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：