小型工业纯钛十字形试件的优化设计毕业论文
2020-04-15 17:39:36
摘 要
在实际情况中,大部分板料的变形是受到双向应力作用的,进行双轴拉伸测试更有利于反映真实的受力情况。同时,双轴拉伸实验可以实现复杂的加载路径,更有助于研究材料变形行为。双轴拉伸十字形试件设计对双轴拉伸实验具有重要意义。通过对十字形试件的优化设计,可以满足双轴拉伸实验对十字形试件受力的要求,使试件的破坏出现在减薄区,以及测试区应力应变尽可能均匀。进行双轴拉伸实验模拟分析前,要通过单轴拉伸实验得到材料的特性参数,进行有限元建模时输入软件中。
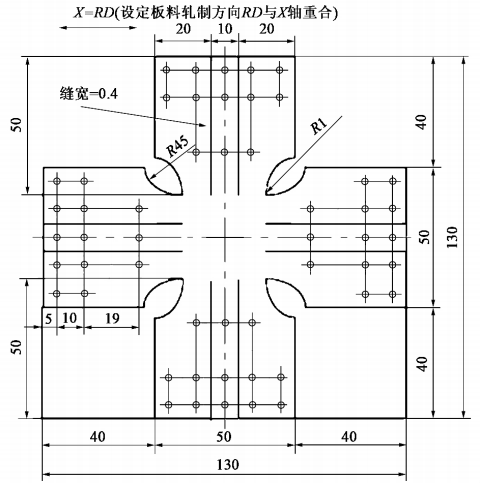
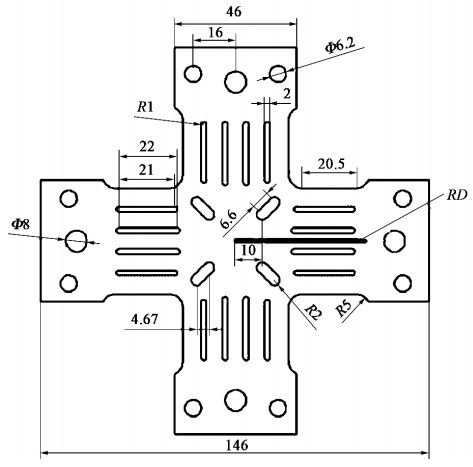
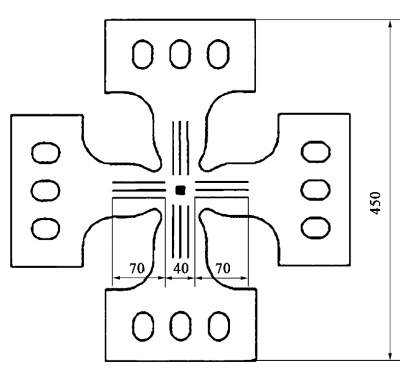
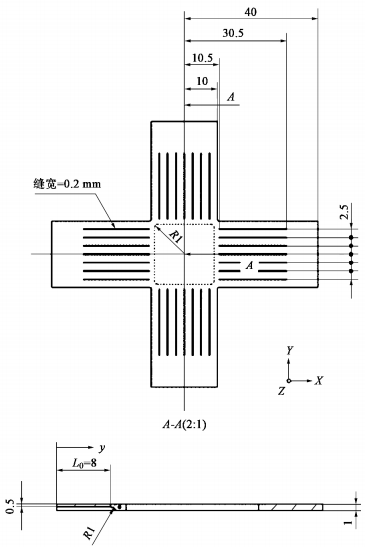
本文设计了带内倒角的中心减薄的臂上开缝型十字形试件。使用ANSYS有限元模拟软件模拟了仅在单因素变化时的试件以及正交实验设计表中的试件,并配合数字图像相关技术(DIC)进行双轴拉伸试验验证,得出结论:
(1)通过研究仅改变单个因素的情况,中心区减薄对试件中心区变形程度增加和均匀度提高有利,中心区与臂交界处受力状况变差,中心区厚度应适中。缝宽对中心区应力及其分布影响不大,缝宽可以选择较大或较小,但考虑到经济因素选择较大的缝宽。缝长改变对试件变形程度的影响较明显,对应力及其分布有较小的影响,选择较长的缝长。缝条数增加,中心区受力均匀度得到改善,缝条数取较多较好。圆角半径过大会对试件中心区mises应力分布的均匀性产生不利影响,圆角半径要取较小尺寸。
(2)通过正交实验设计及分析,得到各因素对中心区均匀度影响最小的值,分别是,中心区厚度0.8mm,缝宽0.8mm,缝长20mm,每条臂上5条缝,圆角半径0.5mm,再结合实际情况,如经济性和加工难易性,得到最优试件A3B4C4D3E1。
(3)通过对比双轴试验结果和有限元模拟结果,可以得到实验结果与有限元模拟结果具有一致性,试件A3B4C4D3E1是最优试件。
关键词:小型十字形试件 有限元模拟 双轴拉伸 数字图像相关技术 正交实验
Optimal Design of Miniaturized Cruciform Specimen for Biaxial Testing of TA2 Alloys
Abstract
In the actual situation, most of the deformation of the sheet is subjected to biaxial stress, and the biaxial tensile test is more conducive to reflecting the true stress. At the same time, the biaxial tensile test can realize complex loading paths, which is more conducive to the study of material deformation behavior. The design of miniaturized cruciform specimen is of great significance for the biaxial tensile test. By optimizing the design of the cruciform specimens, it can meet the requirements of biaxial tension test for the stress of the cruciform specimens, so that the failure of the specimens occurs in the central thinning gauge and the stress and strain in the test zone are as uniform as possible. Before the simulation analysis of biaxial tension experiment, the characteristic parameters of the material are obtained by uniaxial tensile test and input into the software for finite element modeling.
In this paper, a slit cruciform specimen with inner chamfer and center thinning is designed. The ANSYS finite element simulation software was used to simulate the specimens in the orthogonal experimental design table and the single factor change. Use the digital image correlation technology (DIC) to verify the biaxial tensile test and the conclusion was drawn:
(1) By studying only the single factor, the central zone thinning is beneficial to the increase of the deformation degree and uniformity of the central part of the specimens, and the stress state at the junction of the central zone and the arm is worse, and the thickness of the central zone should be moderate. The slit width has little effect on the central zone stress and its distribution, and the slit width can be selected to be larger or smaller, but a larger slit width is selected in consideration of economic factors. The change of the slit length has a significant influence on the deformation degree of the specimens, and has little influence on the stress and its distribution, and a longer slit length is chosen. With the increase of the number of slits, the uniformity of the force in the center area is improved, and more slits are better. Excessive fillet radius has a negative impact on the uniformity of Mises stress distribution in the center of the specimen. The fillet radius should be smaller.
(2) Through the orthogonal experimental design and analysis, the minimum influence of each factor on the uniformity of the central area is obtained. The thickness of the central area is 0.8mm, the width of the slit is 0.8mm, the length of the seam is 20mm, and 5 seams on each arm. The fillet radius is 0.5mm, and combined with the actual situation, such as economy and processing difficulty, the optimal specimen A3B4C4D3E1 is obtained.
(3) By comparing the results of the biaxial test and the finite element simulation results, it can be concluded that the experimental results are consistent with the results of finite element simulation, and the specimen A3B4C4D3E1 is the best one.
Key Words: Small cruciform specimens; Finite element simulation; Biaxial stretching; Digital image correlation technology; Orthogonal experiment
目 录
摘要 I
Abstract I
第一章 绪论 1
1.1 引言 1
1.2 国内外研究现状 1
1.2.1 十字形试样中心区应力确定及试样优化方法 1
1.2.2 十字形试样优化设计实例 2
1.2.3 十字形试样双轴拉伸试验有限元模拟分析及实验 9
1.2.4 较优方案判断标准 9
1.3 选题的依据和意义 9
第二章 几何参数对试件中心区受力及变形的影响 10
2.1 有限元模拟计算 10
2.1.1 几何模型的建立及网格划分 10
2.1.2 材料模型及设定 10
2.1.3 计算参数的设定 11
2.2 中心区减薄量对中心区受力及变形的影响 11
2.2.1 中心区减薄量对中心区最大变形量的影响 11
2.2.2 中心区减薄量对中心区应力分布及大小的影响 12
2.2.3 不同中心区减薄量下试件45°方向上各取样点的应力 15
2.3 缝宽度对中心区受力及变形的影响 15
2.3.1 缝宽度对中心区最大变形量的影响 16
2.3.2 缝宽度对中心区应力分布及大小的影响 16
2.3.3 不同缝宽度下试件45°方向上各点的应力 17
2.4 缝长度对中心区受力及变形的影响 18
2.4.1 缝长度对中心区最大变形量的影响 18
2.4.2 缝长度对中心区应力分布及大小的影响 18
2.4.3 不同缝长度下试件45°方向上各取样点的应力 20
2.5 缝条数对中心区受力及变形的影响 20
2.5.1 缝条数对中心区最大变形量的影响 20
2.5.2 缝条数对中心区应力分布及大小的影响 21
2.5.3 不同缝条数下试件45°方向上各取样点的应力 23
2.6 圆角半径对中心区受力及变形的影响 24
2.6.1 圆角半径对中心区最大变形量的影响 24
2.6.2 圆角半径对中心区应力分布及大小的影响 24
2.6.3 不同缝条数下试件45°方向上各取样点的应力 26
2.7 本章小结 27
第三章 十字形试件正交实验设计分析 29
3.1 中心区域应力均匀度 29
3.2 正交实验设计方案 30
3.3 STATISTICA软件求解各因素的影响趋势 31
3.4 本章小结 32
第四章 拉伸试验测试 33
4.1 实验材料与试样的制备 33
4.2 工业纯钛拉伸的力学性能 33
4.2.1 单轴室温拉伸试验 33
4.2.2 实验数据处理 35
4.2.3 数字图像相关技术(DIC)的原理 38
4.2.4 数字图像相关技术有效性的验证 39
4.3 钛材的双轴拉伸试验 39
4.4 数字图像相关技术(DIC)读取试件应变 40
4.5 试验结果与模拟结果对比分析 41
4.6 最优试样几何形状 42
4.7 本章小结 42
第五章 总结 44
参考文献 45
致谢 47
第一章 绪论
1.1 引言
工业纯钛指钛含量不低于98%且含有少量的氢、氧、氮、硅、碳和铁等杂质的钛。工业纯钛密度是4.51g/cm3,熔化温度范围在1640~1671℃,无磁性,导热系数偏低,具有低密度、高强度、易于熔焊及钎焊等优点,有优良的工艺性能,且塑性好,抗氧化性优。工业纯钛还具有优良的低温冲击韧性和抗腐蚀性能。从1948年以来,钛的应用获得了迅速的发展,同时也有了显著的社会效益及经济效益,钛金属渐渐成为化学工业、石油化工等方面中不可或缺的工程材料[1]-[3]。
板壳结构被广泛应用在工程实例中,但在板料成形过程中,由于实际情况的复杂性,单轴拉伸试验不能反映板料真实应力情况,且设计、模拟等都需要准确的材料的相关数据,因此,材料性能试验选用双轴拉伸法更优。
十字形试件的双轴拉伸可以实现较复杂的加载路径,是研究板料后继屈服行为和成形极限的手段[4]。早在20世纪60年代就提出了下面3个要解决的关键性问题[5]:1)十字形双轴拉伸试件设计制造;2) 通过控制实现平面双轴拉伸的复杂加载;3)试件中心区域应力和应变计算。
1.2 国内外研究现状
十字形双轴试件设计是双向拉伸实验应用的一个难点。为了可以同时保证,十字形试件双臂上的力除以横截面积直接计算出中心区的应力分量,且该应力分量为x和y方向的主应力,需要试件中心区变形始终保持均匀。试件双轴拉伸时,试件臂是传力区,为单向拉伸状态,中心区是双轴拉伸的状态。试件单轴拉伸时变形能力远小于双轴拉伸时的变形能力,所以断裂一般发生在试件臂上。为了在试件中心区获得较高的应力水平,需要避免相邻两臂过渡区应力集中,还可以加强臂的强度或降低中心区域的厚度。
1.2.1 十字形试样中心区应力确定及试样优化方法
可以通过载荷除以中心区横截面面积,得到轴向正应力(它是基于认为中心区横截面所受载荷与臂上的正载荷相等,且中心区剪应力影响可忽略,应力分布均匀)或有限元模拟结合试验再进行修正的方法,求得中心区正应力[6]。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: