英语原文共 11 页

瓦楞纸板在准静态载荷下破坏的理论与实验研究

李学|王军|高德|李伟梁

摘要：本文提出了2个数学模型来预测瓦楞纸板的初始峰值应力和高原应力, 并将其简化为纵向压缩下的正交各向异性板。由此产生的应力应变曲线表现出初始加劲阶段和长平台阶段, 在这种阶段, 决定板的边缘挤压阻力和最大冲击能量的初始峰值应力将被长高原阶段所吸收。通过对板壁弹性屈曲的分析, 得到了预测初始峰值应力的模型, 并根据瓦楞纸板的逐步压缩过程和节能原理建立了高原应力模型。并通过与实验预测值的比较, 对所提出的模型进行了实验验证, 显示出总体上的良好一致性。结果表明, 所提出的模型可用于瓦楞纸箱的设计和瓦楞纸板缓冲包装。

关键字：瓦楞纸板, 设计, 初始峰值应力, 机械模型, 高原应力, 准静态压缩

1引言

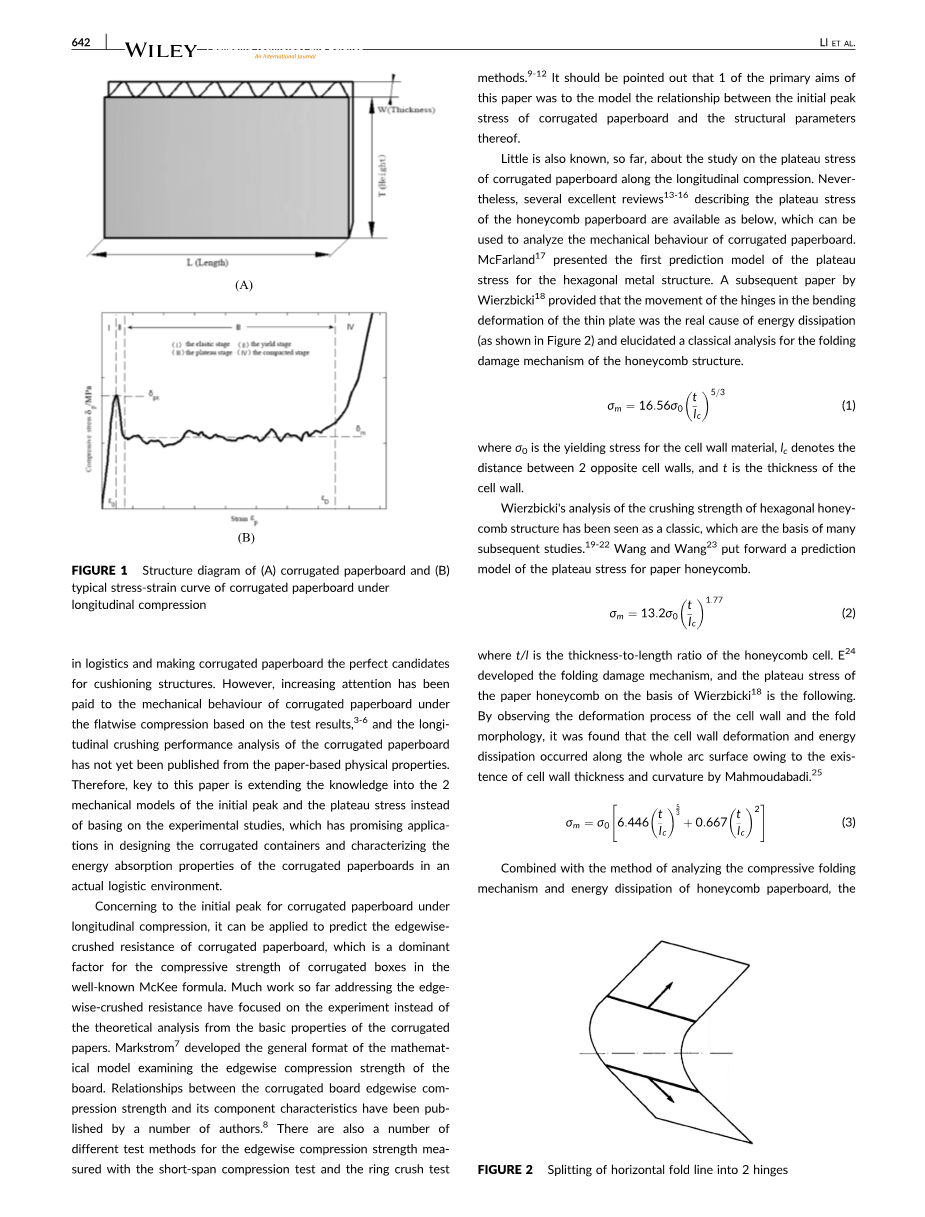
瓦楞纸板等纸基材料由于其高能量吸收能力和轻质性能，已广泛应用于配电包装中作为能量吸收剂或缓冲材料，以保护产品免受外部影响。瓦楞纸箱设计中的影响及其研究也很重要.1,2纵向压缩（外力作用）在T方向上，如图1A所示，是运输过程中的常见装载条件，其中瓦楞纸板可以逐步折叠。合成的应力 - 应变曲线沿T方向压碎显示4个变形阶段（如图1B所示），其中初始峰值应力delta;pk决定了边缘抗压性并实现了最佳设计的瓦楞纸板，而长期高原阶段的平台应力delta;m对抗外部有显著负载。

物流和瓦楞纸板是缓冲结构的理想选择。然而，基于试验结果，瓦楞纸板在平面压缩下的机械性能受到越来越多的关注，并且瓦楞纸板的纵向破碎性能分析尚未从纸基物理性质公开。因此，本文的关键是将知识扩展到初始峰值和平台应力的2个力学模型，而不是基于实验研究，这在实际的物流环境中瓦楞纸箱的设计和瓦楞纸板的能量吸收特性的表征方面具有广阔的应用前景。

关于瓦楞纸板的初始峰值纵向压缩，它可以应用于预测瓦楞纸板的边缘抗冲击性，这是麦克公式中瓦楞纸箱抗压强度的主导因素。到目前为止做了很多工作解决边缘问题 - 抗冲击力集中在实验上，而不是从瓦楞纸板的基本属性进行理论分析。 Markstrom开发了数学模型的一般格式，检查了边缘压缩强度板。瓦楞纸板边缘压缩强度与其组件特性之间的关系已经被许多作者发表.对于边缘也有许多不同的测试方法。通过短压缩试验和环压试验方法测量压缩强度.应该指出的主要目的之一是本文对瓦楞纸板初始峰值应力与其结构参数之间的关系进行了模型分析。

图一：（A）瓦楞纸板的结构图和（B）瓦楞纸板在纵向压缩下的典型应力 - 应变曲线

到目前为止，关于沿纵向压缩的瓦楞纸板的平台应力的研究还知之甚少。 然而，几个优秀的评论描述了蜂窝纸板的高原应力，如下所示，可用于分析瓦楞纸板的力学行为.McFarland提出了六角形金属结构的平台应力的第一个预测模型。随后的一篇论文Wierzbicki规定，铰链在薄板弯曲变形中的运动是能量耗散的真正原因（如图2所示），并阐明了蜂窝结构折叠损伤机理的经典分析。

其中sigma;0是细胞壁材料的屈服应力，lc表示2个相对细胞壁之间的距离，t是细胞壁的厚度。Wierzbicki对六角蜂窝梳结构抗碎强度的分析被认为是经典，这是许多后续研究的基础. Wang和Wang提出了纸蜂窝平台应力的预测模型。

其中t / l是蜂窝单元的厚度比率。 E开发了折叠损伤机理，基于Wierzbicki的纸蜂窝平台应力如下：通过观察细胞壁的变形过程和折叠形态，发现细胞壁变形和能量耗散发生。 由于Mahmoudabadi的细胞壁厚度和曲率的存在，沿着整个弧面。

结合蜂窝纸板压缩折叠机理和能量耗散分析方法，得出瓦楞纸板沿纵向压缩的准静态破碎行为。本文从Wierzbicki18和E24的作品中汲取灵感。 结果，2个数学模型预测瓦楞纸板的初始峰值应力和平台应力推导，与实验数据吻合，可用于瓦楞纸板的设计和瓦楞纸板的缓冲包装。

图二：将水平折叠线分成2个铰链

2造型

2.1初始峰值应力的模型 瓦楞纸板

在本文中，特别关注的是通过粘合波纹芯纸波形成的3层瓦楞纸板（如图1A所示），其波纹和结构尺寸与板的抗边缘抗压性有关。 首先，瓦楞纸板分区结构（图3）可以看作是类似的正弦波曲线和a直线相互连接，其中t0表示波纹芯纸的厚度，t1是外纸的厚度，t2是内纸的厚度。 此外，t1和t2的参数可以用t0表示，t1 = at0，t2 = bt0。根据Timoshenko的弹性稳定性理论。可以出现纵向压缩下的板壁弹性屈曲，并可以计算出板壁弯曲变形的抗弯刚度。

其中D是面板的抗弯强度，r是曲率半径。

图三：瓦楞纸板结构图

图四：瓦楞纸板的简化模型

瓦楞纸板的单元由图5中的3个矩形板组成，表明屈曲载荷主要取决于面积惯性矩和板的宽度。

其中P是屈曲载荷，E是面板的杨氏模量，gamma;是面板的泊松比，t是面板的厚度，K是常数，它是另一侧的约束因子。 如果面板被简单地支撑（自由旋转）并且其具有比l更大的深度T（Tgt; 3l），则K = 2.如果面板被完全夹紧，则K = 6.2。 瓦楞纸板的面板既不是完全自由的，也不是刚性夹紧，因此大约K = 4弹性屈曲载荷是每个面板上的载荷之和，因此弹性屈曲应力可以表示为

其中参数a表示外纸厚度与瓦楞纸芯厚度之比，t1 = at0，E1为外纸的杨氏模量，gamma;1为外纸的泊松比

鉴于外层纸和内纸之间瓦楞纸板材料的不一致性，可以得出：

其中参数b表示内纸厚度与瓦楞纸芯厚度之比，t2 = bt0，E2是内纸的杨氏模量，而gamma;2是内纸的泊松比。 这是一个简单的公式，将初始峰值应力与波纹芯纸的杨氏模量，外部和内部纸张，泊松比，厚度和波纹结构的参数相关联。

图五：纸板墙的纵向屈曲

2.2 瓦楞纸板高原应力模型纸板

2.2.1 变形机制

试验结果表明，经过准静态压缩的瓦楞纸板具有类似的逐步破碎特性。 当瓦楞纸板在纵向压缩载荷下经历短线弹性变形时，瓦楞芯纸和表面纸出现局部屈曲（如图6A所示）。 然后，corru-gated纸出现第一个折叠（如图6B所示），当压缩继续时压碎，第二个折叠开始形成，等等，如图6C，6D）所示。 最后，瓦楞纸板完全变平，进入压实阶段，如图6E所示

2.2.2 典型的折叠机制

当瓦楞纸板在纵向压缩下被压碎时，波纹芯纸逐渐折叠距离2H，即折叠的波长，这可以通过将纸板厚度T除以折叠数n（2H = T / n）得到。 如图7所示。瓦楞纸板的单元如图5所示，其中l是凹凸不平的纸板单元的边长。

图七：波纹芯的渐进折叠

鉴于折叠机构的周期性，可以采用1折作为图8A中的示例，其被定义为V型元件，并且其中长度为2l，theta;是V型元件的角度， t0是波纹芯的厚度。 从图8B可以看出，当V型元件经受纵向加载时，波纹芯经历弹性变形，一旦第一次折叠出现就结束，然后V型元件根据方向具有塑性弯曲变形。 箭头 alpha;，beta;和gamma;分别是面板从垂直方向，弯曲过程中上下单元壁以及倾斜塑料铰链和水平线之间的角度。 s是V型元件的水平位移。 可以使用几何关系

在弯曲变形过程中，V型元件从图8A，B逐渐变化。随着粘合线EFG和纸张的分离，在细胞壁上出现2条倾斜铰链线（GF1和EF1）， 细胞壁中间有2条水平铰链线（BF1和F1I），形成梯形元件（ABF1E，BCGF1，EF1IH和IJGF1）。 考虑到角度theta;在变形过程中保持不变，线BF1和F1I可以在水平方向上移动并逐渐变成2条塑料铰线（如图8C所示），这可以形成圆柱形表面。 4个梯形面与倾斜圆柱面的交点为滚动变形区域。

图六：瓦楞纸板的压缩渐进过程

图八：瓦楞芯的典型折叠机构

2.2.3能量耗散的计算

图9B中纵向压缩下瓦楞纸板的单元壁的折叠旋转模式表明，由于单元壁的厚度和曲率的存在，单元壁的变形和能量的消散沿着整个弧面。 细胞壁的旋转角度从pi;/ 2变为pi;/ 2 omega;。 因为omega;是一个小值，所以sinomega;= b / H.忽略部分破损所需的能量粘性，V型元件折叠过程中的能量耗散是水平铰链线形成过程中耗散的能量，倾斜塑性铰链线形成过程中耗散的能量，以及环面延伸过程中耗散的能量。此外，还应考虑纸张内外水平铰链线上的能量耗散。水平铰链线形成时消耗的能量由于水平铰链线的移动，能量耗散率为

其中alpha;_和L是旋转速率和塑料铰链线的长度。 M表示每单位长度芯纸的完全塑性弯曲力矩（M0 =delta;0t2/ 4）。 delta;0，delta;1和delta;2的参数分别是芯纸，外纸和内纸的屈服应力。 每卷芯纸的全塑膜力可表示为N0 =delta;0t。考虑到瓦楞纸板的折叠损坏机理（如图8C所示），总共有8条水平铰链线，其中6条铰链线的长度为l，厚度为t0，2条铰链线为l - H长度为gamma;，厚度为t0

塑性铰链线的旋转角度为[0，pi;/ 2]。 能量E1可以通过如下积分获得：

其中c1 =4pi;，c2 =-2cottheta;4，等式（11）可以如下获得：

图九：瓦楞纸板的细胞壁折叠图。 A，细胞壁的经典折叠模式。 B，圆柱曲率对细胞壁折叠模式的影响

同样，能量消散在水平铰链线上内外纸分别为E2和E3

其中M1和M2表示每个完全塑性弯矩外纸和内纸的单位长度

.M1 =mu;M0，M2 =theta;M0。 l1和l2分别是外纸和内纸的塑料铰链线长度

假设c3 =2pi;·2sintheta;2·mu;; c4 =2pi;·2sintheta;2·v。 公式（13）可以简化为

倾斜塑料铰线形成时消耗的能量由于倾斜的移动导致的能量耗散率塑料铰链线是

其中L和alpha;m分别是倾斜塑性铰线的长度和曲率。

其中b是环形表面的半径（如图8D所示）

如图8C所示，2个倾斜的塑料铰链线的长度为2H /singamma;，厚度为t0

倾斜铰链线的能量耗散率为

能量E4可以通过如下的[0，pi;/ 2]上的积分alpha;获得

当，计算得

环形表面延伸过程中的耗散能量鉴于折叠过程中的不确定因素，塑性流动面积与H，b和rho;30（如图8和10所示）有关，在简化理论中描述 V型元素

可以获得塑性流动区域中膜应力delta;0t0的积分。 因此，环形表面延伸期间的耗散能量为：

当c6 = 4rho;时，E5可表达为：

2.2.4瓦楞纸板的高原应力

假设在压缩过程中能量守恒，3种类型的总能量耗散是：

将等式（12），（14），（19）和（21）代入上述公式（22），得到以下等式：

根据和

另外，皱纹元素的面积是

因此，随着高原应力的定义，公式（24）除以公式（25），得出：

图十：折叠单元的塑料流动区域

当

时

上面的公式可以写成

上述等式是一个简单的公式，将高原应力与波纹芯纸，外纸和内纸的屈服应力以及厚度与长度比相关联。

3 实验研究

3.1瓦楞纸板样品和方法

用于制造瓦楞纸板芯的瓦楞芯和瓦楞纸均由Worthpack材料集团（中国上海）供应，包括170克/平方米的芯纸，170克/平方米的外纸和160克/平方米的内部 文件。 样品的主要区别是瓦楞纸板的孔格类型，具有A型，B型和C型，其边长分别为4.02,3.41和3.81mm。 所有样品均在23plusmn;1℃，50plusmn;2％相对湿度的环境中预处理24小时，符合中国国家标准GBT 10739-231，其厚度可用GB / T451.3-232和 GBT6547#39;8.33试样的规格和特性列于表1和表2中。

3.2实验

无可否认，瓦楞纸的机械性能具有各向异性，易于弯曲，边缘压缩强度低。 鉴于通过压缩试验难以获得弹性模量和屈服强度，一般方法是使用纸张的拉伸性能而不是其压缩性能.24测试设备包括LRX Plus通用材料试验机和THS -AOC-100AC恒温湿度箱（中国轻工业包装制品质量监督检验中心，江南大学）。

由于获得了屈服强度（如图11所示），瓦楞纸被测试，其被定义为与小塑性变形相对应的应力，其通常基于经验或材料的实际特征来确定。 根据标准GBT450-200834和GBT1040.1-2006.35，对所有规格进行预处理并切割成相同的区域，长度为12.7times;152 mm，长度为65 mm。值得注意的是，考虑到纸张的垂直和水平性能，标本 要求纸张垂直方向增加腐蚀纸板的强度。

瓦楞纸板在准静态纵向压缩下进行测试，以确定初始峰值和平台应力（如图12所示），其尺寸为100times;100 mm。 并且进行测试以压缩在12plusmn;2 mm / min的恒定位移速度下，试样达到原始厚度的85％，每个规格取5个试样，并按推荐标准GBT450-200833和GBT654

资料编号：[4164]